同余算术在建筑工业中的应用-为了保证余数关系的正确性

这一章我们讲“同余算术”。这个话题中最关键的一个概念叫作“模”。在讲授数学之前，我们先轻松一下，说一个关于“模子”的趣味历史故事。

明朝后期有一个很聪明的基层官员叫作杨云才，他在荆州任职时，有一回省政府指示荆州扩建城墙。当工程设计、预算及工期都已经获得批准之后，省政府突然下发文件，命令将城墙在原规划基础上再增厚二尺。工程的主管官员非常着急，因为如果申请增加经费，报批过程将会拖延工期，导致工程无法按时完成，这可是会让他受处分的事情。于是，他召集下属开会商量。会上，杨云才轻描淡写地说：“领导不用着急，我有一个不增加开支的办法，所以我们不需要重新申请经费。”

第二天，杨云才来到承包城墙墙砖生产的砖厂，声称检查工作，让厂长把墙砖模子拿来给他检查。看了两眼后，杨云才指责厂长的模子不合规格，将其狠狠地摔碎在地上。然后，他取出自己预先准备好的模子交给厂长说：“你那个模子不行，要照这规格烧制。”厂长察看杨云才的模子，觉得和原先的模子没有什么差别，于是承诺照办。

事实上，杨云才的墙砖模子比正常的尺寸加宽了二分，这光凭肉眼看不出来，但它累积起来的砖块厚度，恰好可以满足省政府增加城墙尺寸的要求！结果，城墙扩建工程如期完成，在没有增加开支的情况下，达到城墙加厚两尺的要求。

我们必须说，上级不改工期而突然下命令的做法是无理的，杨云才是聪明的，但是耍计谋欺骗砖厂是不厚道的。我们讲这个故事，不是赞赏欺骗，而是因为我们下面的数学将从建筑工业里的“模”讲起，所以才先讲一个关于“模”的故事。

建筑工业中其实经常用到同余算术。设计师、建造者甚至木匠和泥瓦匠，他们从来没有研究过数论，却每一天都在用它——出于纯粹的经济原因，现代工业的工作方法中引入了曾经是抽象的、纯理论的“模”的记号。

如果一堵预制墙的尺寸是6尺，建设者就将这个数作为“模”，然后在建筑的各个单元寻找适合它的尺寸。建筑师设计所有墙的长度时，会尽可能使它们成为6的倍数。如果它们符合这个模，那么砖瓦、窗户及建筑的其他各部分就能以最省事的方式组建到一起。

然而，人们并不总是能以上述这种方式建造房子。假如木匠在图纸的某处看到一堵8尺的墙，又看到另一堵墙的长度为14尺。他明白，在8尺墙那儿使用一件6尺预制墙体会有2尺的不足，在14尺墙处使用两件6尺预制墙体同样也将留出2尺的空缺。因此，面对这两种情形，需要处理的问题是一样的。具体使用了几件预制墙体毫不重要，那是很容易的事情。重点是那2尺的空缺，它不能使用预制件，只能用某种形式的手工作业来完成。上述两种情况下木匠面对的是同样的“手工处理2尺空缺”的问题，在数论里这一事实可以记成14≡8（mod 6），我们这个式子读成“14与8对模6是同余的”。余数在这里是很关键的，一旦作为除数的“模”确定下来，两个数同余事实上就是两个余数相等。

在后文中我们将经常应用同余。为了让读者们对同余有更清楚的理解，我们下面再提供另一种阐释方式。

假设一个科学家在做实验，他必须明确实验开始以来所耗去的总时间，所以他使用一个计时器来记录实验时间。我们把实验开始的时刻称作“实验室零点”，把实验经过n小时后的时刻称作“实验室n点”，并把这种钟点称为“实验室时间”。假设，当实验耗费的时间达到38个小时的时候——即实验室时间38点时，他发现自己的手表停了，那么他怎么通过实验室时间推算当时的时间是几点呢？如果“实验室零点”正好是午夜零点，那么问题就很简单：他只要把实验室时间除以12，则余数是几就是几点。由于38除以12的余数为2，因此实验室时间38点简而言之就是2点。这等于说，38与2对模12是同余的：

38≡2（mod 12）。

为了搞清楚实验室时间38点是一天中的几点，我们并不需要知道38除以12所得的整商数，只需要知道余数是2就可以了。当然，如果想知道这个时间是上午还是下午，那么考虑除以24是更好的选择。由于38等于1倍的24与14的和，因此38与14对模24同余。这就是说，实验室时间38点是午夜过后14个小时。由于14≡2（mod 12），这意味着它对应的时间是下午2点。也就是说，我们事实上可以由模12方便地得到下午的钟点数。

很明显地，38≡2（mod 12）的另一个含义是：（38-2）是12的倍数——把余数同时从两个数中减去，则所得的数是模的整数倍。我们因此发现，对任何整数k，（38-2）·k也是12的倍数。而这等于说，38k与2k对模12是同余的，换句话说，就是

38k≡2k（mod 12）。

现在我们开始感觉到把同余符号写得与等号相似是有道理的了，因为和等式一样，我们可以在同余式两边乘以同一个数。即是说：

如果a≡b（modm），则有ak≡bk（modm）。在普通的等式中，我们可以将等式与等式相乘，也可以将两个等式相加。显然，我们应该知道对于同余式这些规律是否成立。

假如a≡b（modm）与c≡d（modm）都成立，那么同余式

ac≡bd（modm）

是不是成立？或者说，ac-bd是不是可以被m整除？

由于c≡d （mod m）意味着c-d = km对某个k成立，因此，

ac-bd =a（km+d）-bd

=akm+ad-bd

=akm+d（a-b）。

而由于（a-b）可以被m整除，即a≡b（modm），因此acbd也可以被m整除，所以ac≡bd（modm）成立。

同余式可以相加的证明更加简单：已知对某j，k，等式a-b = jm与c-d = km成立，则将二式相加，即有

（a+c）-（b+d）= （j+k）m，

这意味着

a+c≡b+d（modm）。

下面我们来推导下同余的另一个性质，它的证明比上述两个要优雅。这条性质表述如下：

若a≡b（modm），则a^k≡b^k（modm）。也就是说，我们可以对同余式两边同时取k次幂。当然，k必须是正整数。

证明非常简单：由于a^k-b^k总是可以被a-b整除，而已知a-b可以被给定的模m整除，因此a^k-b^k也可以被m整除——这就是证明的全部。

如果哪位读者不敢相信a^k-b^k总是可以被a-b整除这一事实，那么就请自己用长除法计算一下a^k-b^k除以a-b的结果。这个结果是一个k-1次“分圆”表达式：

a^k-1+a^k-2b+a^k-3b²+…+a²b^k-3+ab^k-2+b^k-1。

如果有读者对长除法不熟悉，那没有关系，看一看下面这个例子就明白了：

作为一种二元关系，同余与普通的相等一样，是一种“等价关系”。意思是说，这种二元关系满足以下三条性质：

（1）自反性：a≡a（modm）；

（2）对称性：若a≡b（modm），则b≡a（modm）；

（3）传递性：若a≡b（modm），且b≡c（modm），则

a≡c（modm）。

将一个数除以m，包含0在内总共只有m种可能的余数。如果我们将所有整数——包括正整数、0以及负整数——用它模m的余数来区分，则所有的整数将被分成模m的“同余类”或“剩余类”。这将无穷的整数集映射到有限个“等价类”。正因此，同余算术在数论中相当有用。举一个例子，由于8，15，22，29等正整数，以及-6，-13等负整数，它们对模7都同余于1，因而属于同一个模7的剩余类。换个说法，模7同余的运算看起来就是：对给定的数目从1数起，数到7的时候就从头再来，然后看最后数到的是几。因此，在模7同余意义下的算术中，8与1在很多意义上是等价的。

在日常生活中，时钟上的算术就是一个同余算术的例子。每过12个小时，我们的计数就从头再来。我们基本上不对钟点数作加法或乘法运算。但如果我们需要做这些运算，则我们需要特殊的加法表和乘法表。然而，这种运算表不会是无穷无尽的，它仅仅是12×12的表格。为避免烦琐，我们下面以模5为例，列出模5的同余运算表：

在数论中，人们经常需要面对非常大的数。如果这些数可以简化为较小但是等价的数，就可以避免很多复杂而费时的劳动，而这正是同余算术的重要贡献之一。我们下面来看几个例子——

例1 试问999999是不是可以被7整除？

后面大家会发现这不是一个毫无意义的问题。这个问题当然用除法就可以解决，但这里我们用同余思想来解答：

999999=10⁶-1，

10≡3（mod 7），

所以10⁶≡3⁶（mod 7）。

但是，3⁶=（3²）³=9³，而9≡2（mod 7），因此，

9³≡2³≡1（mod 7）。

于是，我们得到

10⁶≡1（mod 7）。

这就是说，999999可以被7整除。

例2 证明：任何奇数的偶数次方与1对模8是同余的。

模8把整数分割成8个剩余类。由定义可知，奇数同余于1，3，5，7中的一个。以上四数的平方依次是1，9，25， 49，它们除以8的余数都是1。因此，如果我们将所有这四个可能的同余式两边平方，则得到：任何一个奇数的平方对模8同余于1。由此，任何一个奇数的偶数次方对模8当然也同余于1。

例3 证明：在第3章提到的第五个费马数，即

F₅=2²5+1=2³²+1，

可以被641整除。

我们不想计算2的32次方，这里的证明将避免艰苦的计算——我们以同余为工具：

640=64×10=5×128=5×2⁷≡-1（mod 641）。

将上式两边取四次方，则得

5⁴×2²⁸≡1（mod 641）。

但是5⁴=625≡-16（mod 641），这可以写成

5⁴≡-2⁴（mod 641）。

由于属于同一个剩余类的数在同余式中可以相互替代（这是同余算术的一个定理，读者可以自己证明），也就是说，由已知同余式

5⁴×2²⁸≡1（mod 641），

我们可以推出

（-2⁴）×2²⁸≡1（mod 641）。

所以，

-2³²≡1（mod 641），

2³²≡-1（mod 641），

2³²+1≡0（mod 641）。

当我们展示同余式与等式之间的相同性质时，“等式可以除以等式”这一等式的性质我们一直小心地避开。现在，我们来考虑一下，在什么条件下，同余式两边可以同时约去一个数？即是说，倘若

ab≡ac（modm），

那么，在什么条件下同余式

b≡c（modm）

会成立？

与以往一样，我们在分析的时候将同余问题转换成关于整除的问题。已知条件是：

（ab-ac）可以被m整除，即

a（b-c）可以被m整除。

我们想要的结论是：

（b-c）可以被m整除。

在a与m互素时，上式当然会成立，因为此时如果m不能整除（b-c），则m也不可能整除a（b-c）。但是，当a与m不互素时，我们则无法知道m究竟是否可以整除（b-c）。

例4 （a） 99≡9（mod 10），

11≡1（mod 10）。

这里我们将同余式两边同时除以9，而9与同余式的模（即10）是互素的。

（b） 48≡12（mod 6），

（1） 8≡2（mod 6），

（2） 4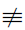1（mod 6）。

这里，符号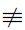的意思是“不同余于”，就像≠意为“不等于”一样。在以上（1）与（2）中，我们将同余式（b）两边同时除以一个与其模不互素的数，（1）保持同余式成立，而（2）则不然。对（b）而言，进一步推导出运算规则并不困难，我们把问题留给读者思考。我们更重视的是（a）这类可以作除法的情形。

现在，我们可以证明一个以费马命名的定理，中文称为“费马小定理”：

定理（费马小定理）若p是素数，a不能被p整除，则有

a^p-1≡1（modp）。

证明：对数集{a，2a，3a，…，（p-1）a}，考虑其中各数将分别落入模p的剩余类中的哪一个。由于模p把所有整数分成p个剩余类，而集合中所有（p-1）个元素都不能被p整除，即都不会落入p的剩余类。不仅如此，因为a与p互素，由同余的除法规律，xa≡ya（modp）意味着x≡y（modp），因此集合中任何两个元素都不同余，也不会落入同一个剩余类。所以，集合中的元素分别落入1，2，3…，p-1的剩余类中的一个。各元素所落入的剩余类未必按照上述顺序，这在前面模5的乘法运算表中可以看到。但无论如何，将这个集合的所有元素相乘，则乘积对模p同余于（p-1）！。也即是说，将所有因子a放在一处，则我们得到

a^p-1（p-1）！≡（p-1）！（modp）。

我们知道（p-1）！不能被p整除，因而与p互素，所以我们得到：

a^p-1≡1（modp）。

如果我们以前就知道这个定理，那么同余式

10⁶≡1（mod 7）

的证明就毫无困难，只要对定理取a=10，p=7就可以了。

我们现在来考察一下二项式展开：

（x+y）⁰=1，

（x+y）¹=1x+1y，

（x+y）²=1x²+2xy+1y²，

（x+y）³=1x³+3x²y+3xy²+1y³，

（x+y）⁴=1x⁴+4x³y+6x²y²+4xy³+1y⁴，

如此等等。以上诸式中x与y的幂呈现的规律很明显，关键的是它们的系数是多少。这些系数读者可能早已知道，它们就是著名的“二项式系数”。从任何给定的一行二项式系数出发，我们不难得到下一行系数。我们按顺序写出多项式的诸系数，用系数行表示多项式，则乘法如下例：

所有二项式系数可以依次列出，则它们很有规律地排成一个三角形。西方把它称为“帕斯卡三角形”，而我国一般将其称为“杨辉三角”：

在上列三角形中，每一行两端的数都是1，而其他的数都由其上一行中的最近的左侧与右侧两个数相加而得。我们用相应二项式的次方数作为行的序号，因此行序号是从零开始的，最高处那个行称为第0行。在这样的记号之下，（x+y）ⁿ展开式的第（k+1）项的系数就是杨辉三角的第n行第（k+1）项，它等于

这个数就是“从n件物品中一次选取k件”的所有组合之总数，在这里它是从n项乘积式（x+y）ⁿ得到k个x与（n-k）个y相乘的所有可能方式的总数。这个公式是初等代数学而不是数论的内容，因此我们在这里略去其证明，有兴趣的读者可以用数学归纳法自行推证。

二项式系数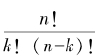通常简记为，但在中学里则经常写成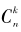，我们的书中一般采用后一种写法。二项式系数有很多有趣的性质，例如它的第二条斜线是自然数列，而第三条斜线上则都是三角形数。这些有趣的内容我们先不谈，因为我们现在要讨论别的问题。

假设我们提出这样一个问题：二项式系数表中会不会存在相邻的两个系数，它们的比值是2/ 3？查看杨辉三角，我们很快发现第四行的4和6符合这个问题的条件。那么，有没有可能还有别的答案？除了同一行中对称位置上的6和4，我们初看时并没有发现其他答案。因此，我们提出更一般化的问题：对给定的分数a，什么时候二项式系数表中的第（k+1）项系数是第k项系数的a倍？

根据以上二项式系数公式，问题等于是求解：

化简上式，易得

n=ka+k-1。

这让人大吃一惊，因为，它告诉我们：答案有无穷多个！事实上，对任何分数a=p/ q，上式即为

因此，只要k的值为q整数倍就可以解得相应的n。换句话说，存在无穷多对相邻的二项式系数，其中一个系数对模q属于同余于零的剩余类。例如，对a = 3/2，只要取k≡0（mod 2）即可。当k= 2时，依上式可得n = 4，这就是我们前面得到的6和4。其次取k=4时，则可得n= 9，即我们在第9行可以得到126 = 3/2×84。接下来是第14行的3003和2002……无论对什么样的分数p/ q，杨辉三角中总有无穷多个符合条件的系数对，这多少有些出乎意料。(www.chuimin.cn)

一个或许更加意义重大的性质是：在杨辉三角第n行的系数中，除了首尾两个1之外，其他数都可以被n整除的充分必要条件是n为素数。因此5和7整除其相应行中除首尾二数之外的所有的系数，而8和9则不然。观察系数公式

立刻可以发现，当n为素数而n>k>1时，分母所有因数都小于n，因而都不能将素数n约去，所以因数n一直保留在分子中。由于系数C是整数，因此它必然是n的倍数。这就是说：若n为素数，则除了首尾二数之外的所有系数都必然可以被n整除。

反之，如果n为合数，则除了首尾二数之外的所有系数中至少还将有一个不能被n整除。事实上，如果n为合数，则它至少有两个素因数。假设n最小的素因数是k，则n可以写成k与一个不小于k的数（未必是素数）m之乘积，即n=k·m。这样，第（k+1）个二项式系数为：

将这个二项式系数除以n，我们得到。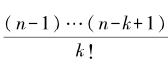

据n=k·m可知，这个数可以写成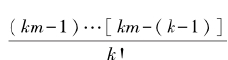。很显然，这个表达式分子中的每一项都不能被素数k整除，因而整个分子也不能被分母整除。也就是说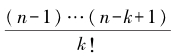，是分数而不是整数，所以相应的二项式系数不能被n整除。

无论如何，n会整除系数中的一部分。那么，我们怎么知道在每一行中，是哪些系数，或者有多少系数可以被n整除？这，是一个具有挑战性的问题。

费马小定理与这个问题紧密相关。我们现在换一种方法，对a用归纳法来证明这个费马小定理。

首先，如果

a^p-1≡1（modp）

成立，则有

a^p≡a（modp）。

这就是说，费马小定理的一个等价的陈述是：“如果p是素数，则a^p-a可以被p整除。”

我们用数学归纳法证明以上等价陈述。当a = 1时， 1≡1（modp），命题显然是成立。现在作出归纳假设：当a取值为某b时命题成立，即b^p-b可以被p整除。接下来，考虑a取值为b+1的情形，即考虑（b+1）^p-（b+1）是否可以被p整除的问题。据二项式展开，我们有

（b+1）^p-（b+1）

= {b^p+[除了首尾两项之外的项]+1}-（b+1）

= b^p-b+[除了首尾两项之外的项]。由于p为素数，我们知道它可以整除上式方括号内的每一项。而由归纳假设，p也可以整除b^p-b。因此，p可以整除（b+1）^p-（b+1）。故定理得证。

杨辉三角

在古代中国，“杨辉三角”首先出现在杨辉1261年所著的《详解九章算术》中。杨辉指出，这个三角出自北宋数学家贾宪的著作，因此我国又将它称为“贾宪三角”。

根据文献资料，贾宪主要活动于宋仁宗时期，因此“贾宪三角”出现的年代为11世纪中叶。这虽然比帕斯卡早数百年，却不是世界上最早的二项式系数三角形。

事实上，古印度天文学家和数学家彘日在公元6世纪中叶就已经对这些二项式系数进行计算，而将它们排列成三角形数表的最早记载出自公元10世纪的哈拉瑜哈，他在注释《檀陀经》时给出了这种三角形，并将其称为“须弥山阶梯”。

注：上图是元代朱世杰在《四元玉鉴》中所画的“杨辉三角”。

稍后于哈拉瑜哈，这个三角形也被巴格达的卡拉吉（约953—1029）发现，而贾宪与波斯人奥马尔·哈亚姆（1048—1131）此后不久也发现了这个数字三角形。因为哈亚姆的贡献，伊朗人至今将这个三角称为“哈亚姆三角”。

这个三角形在欧洲出现得比较晚。德国的彼特·阿皮安（ 1495—1552）是欧洲首位公开发表这个数字三角形的学者，意大利数学家塔塔戈利亚（1499—1557）几乎同时发现这个三角，因而它在意大利称为“塔塔戈利亚三角”。然而，对这个三角研究和应用最为深入的是法国著名数学家布莱士·帕斯卡（1623—1662），西方数学界因而将它称为“帕斯卡三角”。

由于费马小定理可以表述为：“如果p是素数，则a^p-a可以被p整除。”人们自然会考虑这样一个命题：“如果a^p-a可以被p整除，则p是素数。”如果这个命题为真，则它在理论上将成为一个判别素数的准则。当然，如果取a= 2n+1，则由于a^k-b^k总是可以被a-b整除，（2n+1）²ⁿ-（2n+ 1）总是可以被2n整除。因此，这个命题在a取奇数的时候是错误的。事实上，即使不考虑p = a-1的情形，并且将a取为奇素数，这个命题仍然是错误的，例如，11¹⁵-11就是15的倍数，而15并不是一个素数。

奇特的是，如果考虑a = 2的情形，则这个命题绝大多数时候是对的，不正确的时候难得一见。如果我们检查最初的几十个数甚至两三百个数，我们会觉得似乎不会有n为合数却可以整除2ⁿ-2的情形——当n为合数4，6，8，9， 10等等的时候，2ⁿ-2都不能被n整除。事实上，n小于2000时的例外只有五个，而第一个出现在n = 341 = 11×31的时候！难怪人们会觉得费马小定理的逆命题对a = 2的情形似乎是正确的，因为探索性的验算几乎不可能碰上2³⁴¹-2这样罕见的情形。

我们提这个例子，是因为它很好地展现了同余算术的威力。学过对数的读者都知道，2的常用对数lg2≈0. 3010。因此，lg2³⁴¹=341×lg2≈102. 6。这说明2³⁴¹-2是一个103位的十进制数。2³⁴¹-2的值是如此巨大，这意味着具体地计算出它的数值，然后将它除以341，再确定能否除尽的做法，显然是行不通的。然而，同余算术可以帮忙——

由于2⁵=32，2⁵≡1（mod 31），因此我们可以得到

（2⁵）⁶⁸≡1⁶⁸（mod 31），

这等于说，

2³⁴⁰≡1（mod 31）。

同样由于2⁵=32，我们有

2⁵≡-1（mod 11），

因此，我们有

2³⁴⁰=（2⁵）⁶⁸≡（-1）⁶⁸≡1（mod 11）。

综合以上两个结果，我们知道：11与31都是2³⁴⁰-1的素因数，即

2³⁴⁰-1=11×31×某整数。

据此，我们得到

这就证明，2³⁴¹-2可以被341整除。

皮埃尔·德·费马

皮埃尔·德·费马（1601—1665），是法国一位职业律师和业余数学家，与笛卡尔、帕斯卡、梅森同时代，是“梅森学院”的常客。在数学方面，费马对数论、解析几何及微积分都有开创性的贡献。他最著名的猜想，即所谓“费马大定理”，在300多年中极大地促进了数论的发展，直到1995年才最终为英国数学家安德鲁·怀尔斯所证明。此外，费马提出光学中的“最小作用原理”，揭示了光以最短时间方式传播的科学规律，并因此推动了一系列极小值问题的研究。

上面我们看到，不存在自然数a，使得所有使同余式aⁿ≡a（modn）成立的自然数n都是素数。然而，关于费马小定理的探讨还有另外一个角度：有没有合数n，使得同余式aⁿ≡a（modn）对所有自然数a都成立？答案是肯定的。在费马小定理的视角之下，满足这个条件的数和素数非常相像，因此它们有一个名称叫“费马伪素数”。关于这种数的研究在二十年前基本就已经做到尽头，最基本的是如下四个结论：

（1）所有费马伪素数都是至少三个互素的奇素数的乘积；

（2）素因数恰为三个或四个的时候，费马伪素数可以从一些特定的一般表达式中寻找。

（3）一些多因数的费马伪素数可以在较少因数的伪素数基础上构造。

（4）费马伪素数有无穷多个。对充分大的自然数n，小于n的费马伪素数至少有n^1/3个。

三因数的费马伪素数可能出自不同的一般表达式，这类表达式有无穷多个，其中

F₃=（2M+1）（10M+1）（16M+1），

F₃=（6M+1）（12M+1）（18M+1），

F₃=（12M+5）（36M+13）（48M+17）， F₃=（10M+7）（20M+13）（50M+31）

是最简单的四个，如果非负整数M使得某个表达式中的三个因数都是素数，那么这个表达式的结果就一定是一个费马伪素数。例如，上述第二个表达式在M=1时右边的三个因数依次是7，13，19。它们都是素数，因而F₃=7×13×19就是一个费马伪素数。也就是说，对任何自然数a，都有

a^7×13×19≡a[mod（7×13×19）]。

以上结果的问题是：对给定的M，我们需要判断F₃中的每个因式是否为素数，但除了一一验证之外却没有别的办法。这导致我们不知道这些公式中是否包含有无穷多个费马伪素数。然而，已经发现了费马伪素数已经有很多很多了，其中最小的几个是：

3×11×17，5×13×17，7×13×19，

7×13×31，5×17×29，7×23×41。

不难发现，这些数中的前四个可以由上面的公式得到。此外我们需要指出的是，这六个数让我们觉得费马伪素数可能不是很稀有，这是一个误解。现在计算机验算表明，在小于10²¹的自然数中，只有2. 01×10⁷个费马伪素数，比例大约仅仅是2. 01/10¹⁴！

341的素因数是11和31，28的素因数是2，2，7。因此它们是互素的。应用上一章介绍的辗转相除法，则它们辗转相除的结果必然是1：

商为2，余数为0，停止计算，最大公因数等于1。

现在，我们把以上辗转相除用等式重新写，即写成：

341=12×28+5，

28=5×5+3，

5=1×3+2，

3=1×2+1。接下来，我们把最后一个式子写成1 = 3-1×2，然后逐次把后面的式子代入前面，并进行化简，则有：

这就是说，运用辗转相除法我们可以得到：

134×28-11×341=1。

这段演算告诉我们：如果a，b是两个互素的数，则关于x，y的不定方程ax-by = 1有解，并且用辗转相除法可以求得它的一组解。回到同余算术的视角，则我们可以说；如果a与b互素，则同余方程

ax≡1（mod b）

有解，而且它的一个解可以由辗转相除法得到。

中国古代有一个称为“韩信点兵”的趣味数学问题，一个现代汉语的版本是这样的：

有不知数目的士兵，排成三列纵队时，队末只有两个人；排成五列纵队时，队末只有四人；而排成七列纵队时，队末则是六人。问：士兵总共有多少人？

我们将士兵总数记为x，则问题的已知条件是三个同余方程：

x≡2（mod 3），

x≡4（mod 5），

x≡6（mod 7）。

因此，求解“韩信点兵”问题，就是一个求解同余方程组的问题。那么，如何解决这个问题呢？

我们注意到3，5，7两两互素，因此，3与5×7，5与3×7，7与3×5都是互素的。也就是说，同余方程

35x≡1（mod 3），

21y≡1（mod 5），以及

15z≡1（mod 7）

都有解。

应用辗转相除法求解，容易得到：

70≡1（mod 3），

21≡1（mod 5），

15≡1（mod 7）。

现在，我们令

x=2×70+4×21+6×15，

则满足上述韩信点兵问题的三个同余方程。也就是说， x=314是韩信点兵问题的一个解！

细心而有巧思的读者也许会说：补上一个士兵，则士兵数就是3，5，7的倍数了，因此，答案应该3×5×7-1，即104人，怎么我们这里算出了314？其实，这个问题的答案不是唯一的，所有形如105×k+104的数都是问题的解。需要在这里说明的是：仔细推敲可以知道，我们解决问题的方法是有普遍性的，它背后就是数论里著名的“孙子定理”！这是中国人对经典数论为数不多的贡献之一，西方也它归功于中国人，称之为“中国剩余定理”。

孙子定理

孙子定理是中国古代关于一次同余式组求解的定理，国际上通称“中国剩余定理”。这个定理最早以算题的形式出现在《孙子算经》中。目前流传的《孙子算经》成书于中国南北朝时期，大致稍早于祖冲之的时代。

南宋数学家秦九韶在其著作《数书九章》中完善并证明了孙子定理。数百年后，欧拉和高斯都曾得到相同的定理。由于秦九韶的工作被传教士传播到欧洲数学界，因而该定理在欧洲被称为“中国剩余定理”。

原始的“孙子定理”是这样的：

假设m₁，m₂，…，m_n两两互素，那么，同余方程组

有解，其解可以这样来构造：

设M=m₁×m₂…×m_n是整数m₁，m₂，…，m_n的乘积，记

M₁=M/ m₁，M2=M/ m₂，…，Mn=M/ m_n。

找出t₁，t₂，…，t_n，使得

则同余方程组的通解形式为

x=a₁t₁M₁+a₂t₂M2+…+a_nt_nM_n+kM，

其中，k为整数。在模M的意义下，同余方程组只有一个解，即：

x=a₁t₁M1+a₂t₂M2+…+a_nt_nMn（mod M）

我们正文中的例子，就是遵循这个方法求得解答的。

我年轻的时候遇到过一个关于卖生鸡蛋的趣味数学问题，现在我们来看这个问题的一个版本：

一位性格奇特的老汉在农贸市场卖生鸡蛋，他每次只卖出当时拥有的鸡蛋的一半又半个。这样卖了六次之后，他发现剩下的鸡蛋不能再这样卖了，因为“一半又半个”已经不再是整数个鸡蛋了。这时，他提出这样一个问题：他开始卖鸡蛋的时候总共有多少个鸡蛋？

如果最初的鸡蛋个数是N，而卖了六次之后所剩鸡蛋的个数为a，则有a=

将左式去括号然后合并常数项，我们得到a=

我们以前用到过等比数列求和公式，将上式方括号内的数用这个公式求和，即有

移项、去分母，最终可得

N+1=2⁶（a+1）。

现在，无论（a+1）是什么数，唯一分解定理告诉我们，2⁶作为六个素数2的乘积，必须出现在等式的左边。也就是说， 2⁶必然整除N+1，即

N≡-1（mod 64）。这就是说，无论老汉后来剩下多少鸡蛋，只要他一开始以“一半又半个”的方式连续卖出六次，那么他的鸡蛋总数一定满足上述同余式。

略加思考我们马上知道：老汉在六次之后不能再以“一半又半个”的方式卖鸡蛋，其充分必要条件是剩下的鸡蛋数为偶数。因此，老汉原来的鸡蛋总数为

N=64（2k+1）-1。

显然，问题的解也不是唯一的。取k=1时，我们得到符合问题条件的最小鸡蛋数：191。考虑到一个老人不可能把太多的鸡蛋弄到市场上，我们可以认为191就是这个问题的解。

西方有一个著名的趣味数学问题叫作“猴与椰子”问题，这个问题的解决方式与上述卖鸡蛋问题有些相似。在本章的最后，我们把这个问题留给读者做练习：

五个水手计划在第二天早上均分一堆椰子。一个水手夜里起来，决定取走属于他自己的那部分。在把一个椰子扔给猴子之后，椰子可以五人均分，因此他取走自己的份额，然后接着睡觉。其他四个水手也先后半夜起来，每个人所做的也都与第一个水手一样，都是在扔给猴子一个椰子后将椰子五等分，并取走五分之一。天亮之后，五个水手一起又把一个椰子扔给猴子，然后把剩余的椰子平均分成五份。问：最初的椰子堆椰子的最小可能数目是多少个？