数与素数：唯一分解定理及公因数计算

这回我们先来介绍一个定理：算术基本定理。所谓“算术基本定理”，即一个数可以被分解成一系列素数的乘积，本质上这种分解是唯一的。“本质上”的意思是说——例如，我们不区分2×5×2与2×2×5，把它们看作是相同的关于20的因子分解。这样的话，没有人能够用其他素数，比如3或者7，与其他素数的乘积得到20这个数。这对于相对小的数是很明显的，但定理说它对所有数都成立，无论数的大小。这个定理极为重要，值得我们谈一谈它的证明。

在证明这个定理之前，我们需要另外两个定理，我们把它们称为“引理”。有些人调侃地把引理称为“定理证明中的难点”，这话很多时候是符合事实的。如果一个定理的证明需要某个复杂而困难的推证，它常常被分离出来，作为“引理”单独讨论。

如果两个数除了1之外没有其他公共因数，则我们称它们为“互素”的。互素的数本身未必是素数，15 = 3×5和49=7×7都是合数，但它们除了1之外没有其他公因数，因而它们就是互素的。

引理1.如果若干个数都与同一个数A互素，则它们的乘积也与A互素。

这个引理从互素的定义出发就可以证明：因为这若干个数的相乘不会产生原先没有出现的素因数，因而它同样与A没有除1之外的公因数。

引理2.如果若干个数的乘积可以被某个素数p整除，则这些数中至少有一个可以被p整除。

应用引理1，则这个引理可以用反证法来证明：假设若干个数的乘积可以被素数p整除，但这些数却都不可以被p整除。那么，这些数每一个都与p互素，因此据引理1，它们的乘积也与p互素——这就产生矛盾了。

有了这两个引理，我们现在可以来证明如下的“唯一分解定理”了：

定理（唯一分解定理）每一个合数N都可以表示成素数的乘积，这种表示本质上是唯一的。

假设N有两种因数分解式，也就是说，N可以写成两种素数乘积的表达式：

N=p₁×p₂×…×p_m

=q₁×q₂×…×q_n。

当然，我们现在还不能假设以上两种因数分解方式的因数个数一样多，也就是说，我们并不能肯定地说m=n。然而，由于q₁是p₁×p₂×…×p_m的因子，而p₁，p₂，…，p_m都是素数。因此根据引理2，q₁必然等于p₁，p₂，…，p_m中的一个，因此我们不妨说q₁= p₁——因为必要时我们可以重新编排p₁， p₂，…，p_m的下标。现在，将N的两个因数分解式都约去q₁，则得到的等式

p₂×p₃×…×p_m=q₂×q₃×…×q_n。

重复以上过程，则当所有的q都被约去之后，由相等的关系可知p当然也被全部约去。也就是说，我们证明了N的不同因数分解间的素数因子是相互一一对应的。这，就是“唯一分解定理”的意思。

由于每一个数（大于1的自然数）要么是素数，要么可以唯一分解成的不可再分解的素因数的乘积，因此素数看起来具有某种本质的重要性：它们似乎是数的根本性的构成部件。如果它们确实是数的构成部件，并出现在很多的公式之中，人们可能期望所有的关于数的问题都可以用素数来表述。不幸的是，这在现实中远远不可能做到。看起来很多数的奥秘似乎深藏在一些关于素数的理论问题之中，但是我们并没有能够找到解决的办法。其中的有些问题是非常本质的，以至于连顶级的数论专家都开始怀疑它们可能事实上是没有解决办法的。也许，也许人们提出的是错误的问题，一些被认为重要的素数性质有可能实际上是偶发的、非本质的，甚至是“无意义的”。关于这点，我们以后有机会将会再回头来讨论。

为什么1不算是素数？

我们谈到，每个自然数都可以唯一地写成素数的乘积。如果我们把1算作素数，那么这个定理就不成立了。例如，6=2×3= 1×1×2×3。1如果算作是素数，自然数就可以写成多种“素数”的乘积方式。这显然引起不必要的混乱和不方便。因此，1被单独划分成一类。换句话说，根据素因数的情形，自然数可以分成1，素数和合数三类。

关于1和0

任何数乘以1都不会改变它的值，就是说，对任何数x，我们有x·1= 1·x = x。用数学术语来说，1是乘法的“单位元”。相似地，0是加法的单位元。

有些书会把0当作自然数，这是很不“自然”的。因为，直至中世纪西方才从阿拉伯人那里接受从印度传播出来的观念，逐步把0看作是一个普通的数。而在这之前1000多年，自然数早已是古希腊数学中最重要的研究对象。

给定两个数，人们常常有兴趣探讨它们是不是存在公因数，如果存在的话，公因数是什么？解决这个问题的一个方法是：把这两个给定数都写成素因数分解式，然后比较它们的素因数。然而，欧几里得提出了一个更好的办法，称为“欧几里得算法”。这个算法不仅给出两个数的某些公因数，而且得出所有的公因数的乘积，即最大公因数，或称为“最大公约数”。

欧几里得算法在中文文献中通常称为“辗转相除法”，这是《九章算术》里使用的称呼。湖北江陵张家山在1983年出土了有一部名为《算数书》的数学著作，这部书中出现了辗转相除法，把这个算法在中国出现的时间至少推前至公元前200年。而根据我们对战国晚期中国数学传承的分析，辗转相除法应该是由墨家在战国初期提出的。因此，它在中国与古希腊出现的时间基本相当，所以我们在后文中沿用“辗转相除法”这个中国式的术语。

辗转相除法的算法基础是这样一个简单的事实：如果两个数有公因数p，即两个数都被p整除，则它们的差也可以被p整除。换句话说：假如两个数都是p的倍数，分别记为a·p和b·p，那么它们的差（a-b）p当然也是的倍数。

我们用这个算法来计算114与30的最大公因数。这两个数的差是84，因此这两个数的最大公因数同时也整除84，因而它也是84与30的最大公因数。现在，84与30的差等于54，所求的公因数当然也整除54，因而也是54与30的公因数。再次作减法，54-30=24。接下来，30-24=6，24-6=18， 18-6=12，12-6=6，6-6=0。最后得到零时的那个数6，这就是114与30的最大公因数。

我们在这里作两点说明。首先，这个算法有一个捷径。我们三次从114中减去30才得到24这个比30小的数，而用除法求这个数则要快捷得多，这和乘法是重复的加法是一样的道理。将114除以30，所得的余数即是24，这个余数就是下一个除数。欧几里得与中国古人都是这样做的，这个做法可以写成：

第二点说明更为重要：我们为什么因为得到的余数为零，就知道6是我们要求的最大公因数？这是因为，假如余数不等于零，则说明除数本身不是余数的因数。我们知道，所求的公因数同时是被除数与除数的因数，而除数的最大因数是除数本身，因此在除数恰好可以整除被除数的时候，我们也就得到了最大的公因数，所以我们立即停止计算。而说这个公因数就是最大公因数的原因，是因为假如存在更大的公因数，那么这个辗转相除的算法必然会在更早的阶段结束。

我们前文指出15和49是互素的，这同样可以用辗转相除法证明：

对古人而言，得到一个数的因数分解并非易事，而辗转相除法不依靠对任何一个数的因数分解就可以得到两个数的最大公因数，因此它是一个具有重要意义的算法。

张家山汉简《算数书》

《算数书》是1983年中国考古学家在湖北江陵张家山汉代古墓中发现的竹简。经考证，《算数书》成书于西汉初年吕后时期（前202—前186），比通行版本的《九章算术》要早数百年。

《算数书》是秦朝下层官吏学习基层管理所用数学知识的书本内容的撮抄，它的内容比《九章算术》简略，但涵盖了除了“方程章”以外《九章算术》的其他所有内容。《算数书》与此后发现的岳麓秦简《数》，以及北大秦简《算书》一起，改写了中国古代数学史。这三部竹简证明：《九章算术》的内容形成于战国时期的秦国，它由秦国基层官吏所用的数学教材汇编整理而成。有些研究者认为，这些数学知识经过墨家的严格证明，而墨家取得的数学成就与古希腊大致相当，其年代也基本相同。

《九章算术》共分方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股九章，由西汉初年的张苍和西汉后期的耿寿昌整理成书，后由三国时的刘徽及唐初的李淳风分别注释。《九章算术》是先秦数学的总结性、系统性著作，在中国和世界数学史上占有重要的地位。

我们来天马行空、脑洞大开，提出这样一个的问题：如果我们随机选取两个自然数，那么它们互素的概率有多大呢？如果你能够找个办法，把“所有”的自然数放在一个巨大的搅拌机里搅匀，然后从中取出两个数，你觉得这两个数互素的机会大，还是有（除1之外的）公因数的机会大呢？乍一看，这个问题似乎困难到无法解决，而这恰恰是我们提这个问题的原因。

问题的第一个难点是“所有”。从“所有”自然数中随机选取任意两个数，这究竟是什么意思？这里的“所有”并不具有实际可操作性，因为我们事实上不可能把“所有”自然数放到一个巨大的搅拌机里。我们想到两个替代办法。首先，我们可以想象从所有正整数的集合中随机掉出来两个数这样的情景。但这种想象并不让人满意，很多数学家非常不满意，因为让自然数“随机掉出来”是很难做到的。因此我们转向第二个想法：对自然数的开始部分考察这个问题，例如先考虑1到100，考察从中随机选取两个数为互素的概率问题。然后，接着考虑1到1000，如此等等。在这样做了少数几步之后，我们会发现问题的答案很快就呼之欲出，或者像数学家所说的，趋向于一个极限。对我们这个问题，极限的收敛速度相当快。

在攻克上述问题之前，我们必须武装自己，我们需要的武器包括概率论的一些基本思想及原理等数学知识。

一个事件获得成功结果之方式的总数，除以所有可能结果的总数，称为这个事件成功的概率。例如，抛掷一枚硬币的试验会得到正面与反面两种结果。如果以抛得正面为成功，则所有结果中只有一种是成功的，因此一次抛掷硬币获得正面的概率是1/2。另一方面，一个骰子有六面，因此一次抛掷骰子试验得到1点的概率为1/6。当然，在这里，我们假定试验所用的硬币和骰子都是匀称的，不是搞怪的硬币和出老千的骰子。

因为一次试验的结果只可能是成功或者不成功，因而成功与失败方式的总和等于试验的可能结果的总数。所以，如果p是成功的概率而q是失败的概率，则有

此即是说：

p+q=1，或者q=1-p。

接下来，我们需要了解“独立事件的联合概率”。如果一次抛掷硬币抛得正面的概率是1 /2，那么抛掷两个硬币得到两个正面的概率是多少？倘若我们把两个硬币放在杯子里摇一摇，然后抛到桌面上，则我们认为两个硬币掉下来的方式之间是相互独立的。所以，如果我们简单地考虑这种抛掷可能得到的结果，总共有三种结果：

正面和正面，正面和反面，反面和反面。

由于“正面和正面”是唯一的成功结果，因此抛掷两枚硬币得到两个正面的概率是不是就等于1/3？不是！当然，您也发现错了。因为事实上，可能的结果还有一种是“反面和正面”，这与“正面和反面”是不同的，只要给两个硬币标上记号我们就全都明白了。所以说，正确的答案不是1/3而是1/4。

做“抛掷两枚硬币”实验的另一种方法是：将硬币抛掷一次并记录其结果，然后捡起来再做一次。一次抛掷得到正面的概率是1/2，而在第一次为正面的基础上，连第二次的概率也得到正面的概率就是：1/2×1/2=1/4。

那么抛掷三枚硬币，或者一枚硬币连续抛掷三次，得到三个正面的情况又如何呢？其可能的结果是：

反反反，反反正，反正反，反正正，

正反反，正反正，正正反，正正正。

由于只有“正正正”是成功的结果，因此所求概率等于1/8。

从以上思考可以导出“联合概率法则”：n个“独立事件”的联合概率等于这些事件概率的乘积。对抛掷三枚硬币的问题，我们可以将1/2相乘三次，从而得到1/8的结果。

解答我们本节提出的概率问题，最有力的武器是如下惊人的结果：

第一个括号内是所有自然数倒数的平方和。这个无穷级数的收敛性可以用《大学数学》一年级的知识来证明，事实上它收敛于π²/6。遗憾的是，我们不能在这本小书里介绍证明这个有趣结论所必需的数学工具。但是，请亲爱的读者相信我们的话，因为我们需要这个结果。

在最左边这个无穷级数表达式之后的每一个因子，都是“1减去素数平方的倒数”的形式，因此上述等式的左边是一个无穷乘积。为了说明这个无穷乘积的结果确实等于1，我们来作乘法运算：

显而易见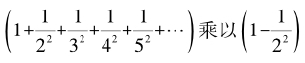，的结果是：无穷级数中所有偶数平方的倒数都被去掉了。接下来：

显然，只要分母是3的倍数的平方，则它们现在也从无穷级数中消失了。我们不需要用乘以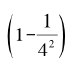来去掉级数中所有分母是4的倍数平方的项，因为它们已经在乘以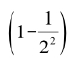时被去掉了。也就是说，我们只需要考虑接下来的素数，即接着乘以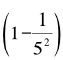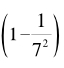，，如此等等。这样接着乘几步，我们就知道乘积的结果等于1加上一个很小的数，而且这个小数随着步数的增加越变越小。事实上，只要乘积的步数足够，我们可以让这个小数任意地小。数学家们概括说，以上无穷乘积依次乘有限步之后的所得称为“部分积”，无穷乘积的意思是部分积的极限，而这个极限等于1。

这样，我们就可以说，

现在，我们终于做好了攻克本段最初提出的问题的准备。我们只要把以上这些数学武器都亮出来，攻克之役就相当容易了。

令m与n为任意给定的两个自然数，而a为任意素数。由于每隔a个自然数就恰有一个可以被a整除，因而所有自然数的1 / a是可以被a整除的。也就是说，m恰好被a整除的概率是1 / a。同理，n可以被a整除的概率也是1 / a。这样一来，m与n同时可以被a整除的概率是1 / a×1 / a。因此，a不能同时整除m和n的概率等于。

m和n互素的意思是它们没有公因子，即它们不被任何一个素数同时整除。根据联合概率法则，m和n互素的概率等于所有形如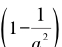的数的乘积，其中的a取遍所有的素数。此即：

容易算出，这个数约等于0. 6079。如果我们考虑从某个有限的自然数集中随机选取两个数，并相应计算其互素的概率，则我们会发现，随着数集规模的增大，这个概率会很快地逼近0. 6079。(www.chuimin.cn)

我们用了很长的篇幅讨论这个问题，它告诉我们这样一个现象：一个问起来很简单的问题可能需要涉及其他领域才能得到解决。我们这个问题涉及的是两个数的公因子，其解答却需要不少初等数论之外的数学。我们需要探究概率论，需要知道关于无穷级数和无穷乘积的收敛问题，并且需要黎曼zeta函数的一个值——这是那个收敛于π²/6的级数的技术性名称。

大学课堂趣闻

四十多年前，华威大学数学教授汉米尔顿在上概率论课时，当场表演掷硬币，他说：“掷硬币的结果无非是正面和反面，两种情形的概率相同，都是50%。”然后，他掏出一枚硬币，抛向空中，结果……落下的硬币直挺挺地竖立在教室的地板上！在全班学生的哄笑声中，汉米尔顿教授一本正经地说：“这种情况出现的概率只有十亿分之一，完全可以忽略不计……”

随机变量

掷硬币和掷骰子都只有有限的几个可能结果，它们是“离散型”随机变量。随机变量的可能取值是一段连续区间时，它就是“连续型”随机变量。

掷硬币出现正面和反面的概率都是1/2，掷骰子出现任一点数的概率都是1/6。连续型随机变量概率的情形是以“分布曲线”形式来描述的，正态分布也称“高斯分布”，是最常见、应用最广泛的连续型概率分布，它的曲线是“正态分布曲线”，俗称“钟形曲线”：

假设一个面包店以每条面包重量一公斤为基准制作面包，但制作中会出现随机误差。那么，称量这个面包店很多很多面包，将不同重量的出现频率画在纸上，就会近似地画出一条以一公斤为最高点的钟形曲线。

庞加莱轶事

庞加莱保持着法国传统生活习惯，他每天早上都到家门口的面包店买一条一公斤重的面包。特别的是，他每天都称他所买的面包并作了记录。过了一年，他的记录给出了一条钟形曲线——正态分布曲线，而平均重量（位于曲线的中点）只有950克。于是，庞加莱叫来警察，警察看了记录之后，对面包店小老板下达了整改警告。又过了一年，庞加莱又叫来了警察，说面包店没有做出整改。面包店老板疑惑地说：“整整一年，我们都挑大的面包给他，他怎么知道我没有整改？”庞加莱拿出记录，只见图形是半条正态分布曲线，只有从950克起的右半边！这证明，他所得到的面包是挑选的结果，而把面包店所有面包考虑在内的话，则情形与去年完全一样，平均分量只有950克。

在上一小节中，我们假定了一件没有证明过的事：素数有无限多个。因而上文乘积式P中形如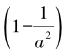的因式有无限多个，乘积永远不会结束。这我们是怎么知道的？我们怎么知道素数不会被穷尽？

证明一个集合有无穷多个元素的方法之一是：给出一个规则或规律，使得对任何一个给定的元素，按照这个规则或规律可以找出一个更“大”的元素（通常是下一个）。正整数集是无穷集合，因为对一个已知的正整数N，无论它有多大，N+1总是一个更大的正整数。

对于素数而言，人们在目前的知识水平上还没有能够作出这种构造性的证明。如果能找到一个只产生素数的公式，甚至仅仅是一个递推关系，那将是一件很令人振奋的事情。遗憾的是，这只是一个奢望。然而无论如何，我们还是能够证明存在无穷多个素数，方法是设法证明不存在最大的素数。其原理在于：任何一个有限的数集必定存在最大数。

证明的方式是反证法。我们暂且假设素数集合中存在最大数，记为N。然后，考虑正整数Q=N！ +1。这里，符号“N！”称为“N的阶乘”，意思是

N×（N-1）×（N-2）×…×3×2×1。

例如，5！ =5×4×3×2×1= 120。现在考察5！ +1，它显然不能被2，3，4，5中的任何一个所整除，因为所得的余数都是1。原因很显然：5！是2，3，4，5的整数倍。因此，我们现在只有两种可能的结果：或者5！ +1本身是素数，或者它有比5大的素因数。同样的道理，取Q = N！ +1，则N要么是一个素数，要么被一个比N大的素数所整除。而无论是哪一种情况，都证明了一个比N大的素数的存在性。这个结果与“N为最大的素数”的假设是相矛盾的，因此我们就证明了：存在无穷多个素数。

以上证明所使用的阶乘是一个常用的运算，它有一个人们通常不喜欢的特点：增长得太快。例如，10！ =3628800，已经是一个超过300万的数字。因此，不喜欢最大素数的阶乘这种大数的人，更喜欢用另一种修正版的反证法来证明素数有无穷多个这一事实。具体的论证过程是这样的——假设素数只有N个，那么我们就可以给它们编号排序，将它们依次记成p₁，p₂，p₃，…p_N。然后，我们取Q=p₁×p₂×p₃×…×p_N+1，则任何Q的素因数都不可能等于p₁，p₂，…，p_N中的任何一个。因此，存在着前述N个素数之外的素数，这与素数只有N个的假设相矛盾。

我们刚说过目前没有产生所有素数的公式。如果能找到性质较差的公式，例如只产生素数的公式——“只产生素数”与“产生所有素数”差别巨大——数学家们也会感到高兴。费马曾经认为他找到了一个：

这个公式产生的数称为“费马数”。把n = 0，1，2，3，4依次代入公式，可得：

确实，以上这些全部都是素数。然而规律马上就被打破，因为

是一个合数。费马没有找出这个数的素因数并不让人奇怪，它的素因数只有两个：641与6700417。人们花了大量时间研究更大的费马数，但迄今为止还没有发现其他任何一个为素数。

读者们可能会好奇地想：费马为什么会提出那么一个式子呢？其中有什么数学上的理由？而F₅是合数这一事实在没有计算机的年代是怎么被发现的？对这些问题，我们可以根据一些数学知识和文献线索来解读。

费马是17世纪的一个法国律师，也许是业务不多，也许是他太喜欢数学，反正他花了很多业余时间在研究数学问题。我们猜测，他在研究产生素数的公式时，首先发现3、5、17分别是F₀、F₁、F₂的形式，因此产生考察形如2^m+1的公式的念头。

然而，形如a^m+1的二项和，当m= 2k+1，即大于1的奇数时，我们有因式分解公式：

因此，2^m+1如果是素数，则它的指数m不能是奇数，也不能有奇数因数。也就是说，如果2^m+1是素数，那么它的指数只能是2的某个次方！大概正是因此，费马才决定考察形如2²n+1的数。而当他认真验算了F₃和F₄之后，他当然倍受鼓舞，因而信心满满地提出了他的公式。

然而，F₅= 2³²+1 = 4294967297，它对古人而言太大了，寻找它的因数是一件很困难的事情，所以费马没有能够做到。据说，第一个对F₅作出因数分解的是伟大的欧拉。那么，欧拉是怎么作出因数分解的呢？文献记载，他用了如下高超而有趣的技巧：

就这样，欧拉得到：

至于6700417是不是素数，欧拉似乎没有给出答案，但后人证明了它是，因而欧拉实际上得到了F₅的完全因数分解。

欧拉的证明技巧显然受到他自己证明的一个定理的启发，他证明：如果某个F_n不是素数，那么它的素因数一定是形如k×2ⁿ⁺¹+1的数。后来，一位名为卢卡斯的数学家把这个素因数的形式改进为k×2ⁿ⁺²+1。基于这个定理，后来研究费马数的数学家们用高深的数论知识和技巧证明了很多费马数都是合数。例如：

上一章我们提到两个产生若干个素数的公式，它们是：

正如我们所说，对x分别等于41及80，以及此后的很多x值，这两个公式所算得的不是素数。

事实上，任何多项式都不可能只产生素数。为了证明这一点，我们使用反证法。假设存在一个多项式

Q（x）= a₀+a₁x+a₂x²+…+a_nxⁿ。

上式中的所有系数都是整数——正整数、负整数或零。系数中的下标都只是记号，而x左上方的数则表示次幂，Q（x）表示将变元以x代入时这个多项式的值。我们的反证假设是：对所有的x，Q（x）的值都是素数。现在，我们取x=b，记其产生的素数为p，即Q（b）= p。然后我们来证明，对所有m=1，2，3，…，p可以整除Q（b+mp）：

Q（b+mp）= a₀+a₁（b+mp）+a₂（b+mp）²+…+a_n（b+mp）ⁿ

将右式的括号展开，则有：

Q（b+mp）= （a₀+a₁b+a₂b²+…+a_nbⁿ）+…

[很多其他项，全部都是p的倍数]。

上式的省略号表示展开式中除前面括号之外所有其他的项，它们每一项都是p的倍数。由于前一个括号中的数正好是p，所以我们得到：

Q（b+mp）= p+p[另一个关于b，m，p的多项式]。

由于m可以取无穷多个不同的值，这个新的关于m的n次多项式也有无穷多个相应的值。

由于p=c₀+c₁x+c₂x²+…+c_nxⁿ是一个n次方程，它最多只能有n个不同的实根。换句话说，对任何给定的数值w，任何一个n次多项式Q（x），最多只能有n个x值使得Q（x）的数值恰好等于w。这样一来，所有Q（b+mp）的值中只有有限个恰好等于p，其他的则不可能与p相等。由于Q（b+mp）有无穷多个，而且它们都是p的整数倍，因此有无穷多个Q（b+mp）的值不是素数——这与反证法假设矛盾！这就证明：任何多项式都不可能只产生素数。

由于古人认识到素数是自然数的关键构件，自古以来人们做了很多关于素数的研究，也因此产生了很多关于素数的猜想。由于华罗庚、王元、潘承洞和陈景润的杰出贡献，对我们中国人而言最著名的猜想莫过于哥德巴赫猜想。除此之外，还有另一个中国人做出了杰出贡献的猜想，它就是“孪生素数猜想”！而这个中国人的名字叫作——张益唐。

古人发现有些素数之间“距离”很近，例如3和5，5和7，11和13，17和19等等，它们之间的差都只有2。因此，古人把相差为2的两个素数称为一对孪生素数。在素数表的开头，孪生素数看起来经常出现。随着素数的增大，孪生素数的出现越来越稀少，但却总能不断地找到。截至2016年初，人们发现的最大的孪生素数对是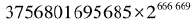-1和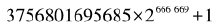，它们是长达200700位巨大数字。

然而找到的孪生素数对再大，也不能证明孪生素数是否有无穷多对。很久以来，是否存在无穷多对孪生素数，一直是一个悬而未决的问题，而“存在无穷多对孪生素数”这个看似正确却无法证明的猜测，就是著名的孪生素数猜想。

由于这个猜想太难，数百年里都没有人能够解决，因此人们转而考虑相对“容易”的问题。首先，对一个给定的偶数N，如果数对p，p+N是一对素数，那么我们就称它们是一对“N-孪生素数”。据此，一位数学家在1849年提出一个相对“容易”的猜想：

存在偶数N，使得N-孪生素数有无穷多对。这个猜想可以称为“广义孪生素数猜想”或“弱孪生素数猜想”。

然而，证明以上这个猜想仍然相当困难，对它的研究在其后的160多年里没有出现突破性的进展。让所有人意想不到的是，在2013年5月，不为数学界所知的数学家张益唐发表了一篇论文，证明了N的存在性。通俗地说，张益唐证明：存在一个小于7000万的偶数N，使得无穷多对形如p，p+N的数对为素数对。

虽然7000万是个很大的数字，但它已经证明了弱孪生素数猜想。而如果人们能把N降低到2，那就等于是证明了孪生素数猜想。因此，张益唐的研究成果激发了数论界极高的热情，很多数学家积极投入到降低N的上界的研究之中。截至2014年上半年，数学界成功地把N降低到不大于246。

张益唐是北京大学数学系78级的学生，1992年在美国获得数学博士学位之后，因为没有获得大学或研究机构的职位而未能成为专业数学家。但是张益唐没有放弃，在困境中仍然把业余的主要精力投入到数学研究中，终于在20多年后一鸣惊人，成为近年来数学界最为引人注目的明星。

亨利·庞加莱

亨利·庞加莱（1854—1912），法国数学家、天体力学家、科学哲学家，在数学及物理学的多个领域都做出杰出的贡献。他是19世纪后期至20世纪初的领袖级数学家，是最后一位对数学和其应用具有全面知识的全能数学家。

关于庞加莱有两件事很突出：一是他提出狭义相对论的时间早于爱因斯坦，二是他在1904年提出“庞加莱猜想”，这个猜想在100年后才由俄罗斯数学家佩雷尔曼证明。

格里戈里·佩雷尔曼

格里戈里·佩雷尔曼出生于1966年，是一位俄罗斯数学家。2002到2003年间，佩雷尔曼在网站上张贴三篇论文，证明了百年来悬而未决的庞加莱猜想。

然而，此后佩雷尔曼辞掉工作，隐居于俄罗斯乡下，淡出公众视野。2006年国际数学联合会将有“数学诺贝尔奖”之称的菲尔兹奖授予佩雷尔曼，但他拒绝领奖。此后，美国克莱数学研究所向他颁发100万美元“千禧年数学大奖”，他同样拒绝接受。

莱昂哈德·欧拉

莱昂哈德·欧拉（1707—1783），瑞士数学家、物理学家，是历史上最伟大的数学家之一，他对数学及物理学的发展都做出了全面而杰出的贡献。欧拉是数学史上最多产的数学家，从19岁到76岁，他在半个多世纪写下难以计数的书籍和论文。早已列入出版计划的《欧拉全集》共84卷，由于资料浩如烟海，至今尚未全部出版。

欧拉的成就是全方位的，几乎每一个数学领域都可以看到欧拉的名字，例如多面体的欧拉定理，空间解析几何的欧拉变换，数论中的欧拉函数，级数论的欧拉常数，微分方程的欧拉方程，变分学的欧拉方程，复变函数的欧拉公式，等等。