前文的分析同时告诉我们,完全平方数的数列中也没有两个项的比例等于2与3之外的任何其他素数,因此素数的平方根都是无理数。此外,虽然6不是素数,一个完全平方数也不会是另一个完全平方数的6倍,因此也是无理数。总之等等都是无理数。实数中有很多很多的无理数,这些无理数中“绝大部分”不是代数数,它们不能表示成任何代数方程的根,我们将这类数称为“超越数”。......
2023-10-30
在蛮荒时代,世界上是没有数字的。有人说数字也许本来就有,只是我们的祖先不知道它们的存在罢了。数字到底是自然存在、本来就有的?还是被人类创造出来的?这,是一个值得探讨的问题。然而我觉得,我们应该把这个问题留给哲学家们去思考,数学史的专家们能肯定的只是——人类文明中,数数这个能力来得比较迟。
19世纪曾经有学者声称某些动物可以数到“5”,这后来被证明是错误的。其实,连早期的人类都没有数到“5”的能力。在一百年前的一些与世隔绝的原始部落里,人们甚至还把多于“3”的数量简单地称作“许多”。
假如我们的世界只有三种数字——“没有”“少量”“大量”,那需要背口诀表的学生们简直要欢天喜地了,因为所有加法只能归为以下几种:
没有+没有=没有
没有+少量=少量
少量+少量=?
没有+大量=大量
少量+大量=大量
大量+大量=大量
但是,这种设计不仅有问题,而且问题还不小:上面公式中的问号揭示了一个难点——当“少量”加上“少量”时,什么时候会“量变产生质变”,从“少量”变成“大量”?类似的困惑催生了计数这门学问,而如何从“没有”“少量”“大量”演变为“1”“2”“3”等等,则更是个漫长的过程。毕竟,数字不是史前少数有学问的祭师在几天时间里就可以琢磨出来的。
古印度人喜欢谈论巨大的数字
古印度人喜欢谈论非常非常大的数字,例如在《华严经》中,梵语“俱胝”指一亿(108),一俱胝的俱胝叫作“阿庾多”(1016),一阿庾多的阿庾多叫作一“那由他”(1032)……
我们摘取《华严经》的一段,让读者看看古印度人谈论多大的数字:“……或刹那入,或须臾入,或相续入,或日初分时入,或日中分时入,或日后分时入,或夜初分时入,或夜中分时入,或夜后分时入,或一日入,或五日入,或半月入,或一月入,或一年入,或百年入,或千年入,或百千年入,或亿年入,或百千亿年入,或百千那由他亿年入,或一劫入,或百劫入,或百千劫入,或百千那由他亿劫入,或无数劫入,或无量劫入,或无边劫入,或无等劫入,或不可数劫入,或不可称劫入,或不可思劫入,或不可量劫入,或不可说劫入,或不可说不可说劫入……”
我们当然知道,人类后来还是琢磨出了计数的学问。然而,如何“计数”是一码事,如何“记数”又是另一码事。古人记数的方式,是经过不断的发展而完善的。
来讲一件我小学低年级时候的故事,它实在让我太震撼,以至于现在的记忆还相当清晰:
数学老师做多位数记数的课堂小测验,要求我们写下他说的多位数。他念道:三百二十一,一千七百五十六,如此等等。在老师发下他批改的小测结果后,我同桌的小玲当场号啕大哭!我伸头一看,发现小玲写的是300201, 1000700506,等等,而每个答案上面都有一个当然的大红叉叉!
很显然,那时的小玲没有十位、百位等“数位”的概念,所以她才把老师说的数写成那个样子。有趣的是,小玲的写法和古罗马人有些相像。古罗马人同样没有数位的概念,他们的记数方式甚至比小玲的还笨拙。
古罗马人用“I”“V”“X”“L”“C”“D”“M”分别表示“1”“5”“10”“50”“100”“500”“1000”。因此,上述321和1 756这两个数字,古罗马人分别写成“CCCXXI”和“MDCCLVI”!这完全就是把“C”“X”等固定字母所表示的数加在一起的方式,很烦琐、很笨拙,是不是?
不过,罗马人有一点比较有意思,他们其实不完全用加法表示数,他们也用减法。例如,“9”这个数固然可以写成“VIIII”,但罗马人一般把它写成“IX”——把“I”写在“X”的左边,表示“X”减去“I”所得的数目。同样的道理,1979一般写成“MCMLXXIX”:最左边的“M”表示一千,接着的“CM”是一千减去一百,“LXX”是七十,而“IX”则表示九。这里我们看到了罗马人的小聪明,但他们的记数方法终究还是太笨拙了。
古代文明中数的进位制
古代文明中,古埃及、古印度以及中华文明都采用十进制,而两河文明则采用六十进制。
“两河文明”指的是在底格里斯河与幼发拉底河之间的“新月形”地带,即美索不达米亚地区的古文明。考古发掘出来的距今5000多年的泥板,向我们透露了这个文明的数学知识。有著名学者认为,两河文明的六十进制是因为使用五进制的族群和使用十二进制的族群融合而产生的。
证据表明,古人类使用的进位制都与人体的构造密切相关,五进制和十进制与手指数目的关系是一目了然的,而十二进制其实也与我人类的手掌紧密相关。
印度—阿拉伯数字
我们现在使用的1,2,3等所谓的“阿拉伯数字”,其实是古印度人发明的。它们在中世纪被阿拉伯人传播到西方,因此被称为“阿拉伯数字”。事实上,它们应该称为“印度—阿拉伯数字”。
古印度人的数字本来是从右向左写的,与现在的顺序相反。后来因为造成的混乱太多,才逐渐过渡至现在的顺序。
罗马记数系统中的数字是用一系列特殊字符表示的,“5”“10”“50”“100”“500”都有特殊的记号。这些记号只是约定的记号而已,没有逻辑没有理由。此外,罗马人没有使用“零”这个符号,这是一个很重大的缺失。
零的重要性不在于它的存在,而在于它的使用。由于罗马计数系统中没有零,所以“V”与“L”是两个没有联系的记数符号。而在我们现在使用的阿拉伯数字系统里,5与 50是有联系的——事实上它们的区别只在于“零”出现的位置。在这种记数系统中,“零”是一个重要的“占位”符号。
小玲所写的“300”,与“3”的差别是右边多了两个零。我们说“0”是占位符号,这里的两个“0”把“300”这个数里面的“3”向左挤了两个位置,所以它成了一个“百位数”。同样一个“3”,写在一个数里的不同位置,所表示的数目不一样。这样一来,记数的符号就整齐而简单多了,这是“数位”的妙用之一。
依照“数位”的用法来记数,在“321”这个数里,“1”在右起第一位即“个位”,所以它表示“1”;“2”在右起第二位即“十位”,所以它表示“20”;“3”在百位,所以表示“300”。因此,整个数表示的就是“三百二十一”。如果小玲懂得数位记数法的意思,她就不会在小测验里错误地写了那么多的“0”,然后面对一堆大红叉叉号啕大哭了。
“数位”的妙处不仅在于记数,它同样大大地便利了数的运算。我们做加减乘除都觉得很容易,就是使用数位计数法的结果。罗马计数方法没有这样的便利,罗马记号下的乘法计算根本就没有简单的办法。无论如何设计罗马计数系统的乘法计算方式,它的算法都是复杂且困难的。对绝大多数罗马人而言,如果他们计算乘积的话,很可能是通过不断重复相加做到的。
罗马数的加法倒不是很困难,事实上和咱们的系统大致相当。首先,将所有的数都改写成没有减法的形式。例如49这个数,为了做加法,应该由XLIX改写成XXXXVIIII。接下来唯一需要做的,就是把字符们放到合适的列上,再注意进位问题就可以了:
中国古人计算时使用算筹,即小竹棍或小木棍。他们把算筹放在有形或无形的格子里,不同格子里的算筹表示的数目不同。例如,右起第一格里(横)放三根算筹表示“3”,而放在右起第三格时则表示“300”。在记录数字的时候,中国古人也模拟算筹的图形来记录。可以说,中国古人在计数与记数时都使用数位记数法。
为了快速分辨数位,古人交替使用横置与竖置算筹的方式表示数字,例如右起第一位的“3”用 表示,而右起第二位的“3”(即30)则用
表示,而右起第二位的“3”(即30)则用 表示。此外,古人还用与小于五的数字方向垂直的一根算筹表示“5”,使得大于五的数字表示不至于太复杂。例如,7036这个数古人记成
表示。此外,古人还用与小于五的数字方向垂直的一根算筹表示“5”,使得大于五的数字表示不至于太复杂。例如,7036这个数古人记成
例子中空的(隐形的)格子表示百位数是零,可见中国古人是有“零”的概念的。当然,由于“零”没有专门的记号,有些时候还是会造成不方便。
顺便说一句,最迟在汉代,中国古人就已经使用红黑两种颜色的算筹,用红色算筹表示负数。也就是说,在古代中国负数概念的出现及其在计算中的运用都相当早。
中国的算筹
古代中国计算中常用算筹表示数字。算筹的摆放分为横式和竖式,竖式用“竖”表示1而用“横”表示5;横式则用“横”表示1而用“竖”表示5。例如,下图中表示的是2086。
古人也用算筹式符号表示数字,上述2086用符号书写,就是: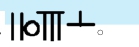
毫无疑问,如今我们都能够熟练地作乘法运算。然而,在当前的数字系统中,乘积的本质是什么呢?这点也许我们中的很多人都没有思考过。
我们来考察207乘以35。我们不直接作数的乘法,而是先考虑两个代数式的乘积:
(2x2+7)×(3x+5)= 6x3+10x2+21x+35。
将x=10代入以上的右式,你会发现,你已经用代数的方式计算出了207×35的结果。这其中的道理是,207所表达的数值就等于2×102+0×101+7+100,这个式子中100的数值等于1,这想想同底数幂相除的运算就可以明白。
数字中的“0”是重要的,207中的“0”占据了数字中的“十位”,使得207区别于27。一次多项式一般按变元的次方数从高到低的次序写成一个和式,这与我们的记数方法一样,只不过一元多项式中“占位”的是变元的次方。2x2+7与2x2+0x+7表示相同的多项式,0x这种等于零的项通常可以不写,正如算筹表达式里的空格子一样。总之,我们的十进制数字系统实际上是一元多项式中以10取代变元所得表达式的简化记录形式。
我们的算术以十进制为基础,因此数值10对于我们是特别到可以说是“神圣”的一个数字。那么,10为什么显得“神圣”呢?事实上,它只是我们所选择的特殊数值,而其根源只不过是因为人类有十根手指,早期人类“掰手指”计数的历史使得10成为算术乃至数学中“神圣”的数目。然而,代数式对变元x是正确的,无论它被选择用10还是其他数值替代,其正确性不会改变。因此,理论上我们可以不用10而使用12或16等其他数值,进而使用十二进制、十六进制等进位制。
事实上,人类历史上出现过十二进制、十六进制、二十进制、六十进制等多种与十进制不同的进位制,它们中有些现在还在人类的日常生活中使用,例如1英尺等于12英寸,1磅等于16盎司,1小时等于60分钟,等等。
历史上的进位制在人类语言中也留有痕迹。英语不仅有dozen(中文译为“打”)这样表示十二的单词,“eleven”“twelve”与“thirteen”“fourteen”等的拼写区别也是十二进制的明显痕迹。法语更有意思,它的数字词汇中存在着十六进制、二十进制以及六十进制的痕迹。例如,法语的十一到十六依次是onze,douze,treize,quatorze,quinze,seize,而十七至十九则为dixsept,dix-huit,dix-neuf,写法的区别昭示着十六进制的历史存在。
法语中数字的表达
在法语中,从10,20,30直到90的写法依次是:dix, vingt, trente, quarante, cinquante, soixante, soixante-dix, quatre-vingts, quatre-vingt-dix。这里,有两点很值得注意:首先,从10到60都是一个单词,但10和20的拼法显然与30到60属于不同体系;其次,70写成“60+10”,80却写成“4×20”,90更是写成“4×20+10”!事实上,这些写法是法语中残存的20进制和60进制的痕迹。
除十进制以外的进位制并非新生事物,但因为二进制计算机的产生,使得它们变得引人注目。
人们认为现代电子计算机几乎可以做任何事情,而事实上它可以说是相当“弱智”。它所能做的是极其基础的:它只是回答诸如某一个给定数是否大于另一个给定数之类的简单问题,而且它的回答只是简单的“是”或“否”。然而,它以极快的速度回答这种问题,然后立即处理下一个简单问题。就这样,计算机按照人类的指令,以无比惊人的速度处理庞大复杂的指令序列。计算机的每个步骤只是回答“是”与“否”,然后把它们正确地组合起来,从而解决复杂的问题。每个“是”由一个“开”信号来完成,而每个“否”则用“关”表示。因此,所有的数值资料都必须被翻译成一系列“开—关”信号,然后再输送给机器。由于这个原因,人们使用“二进制”系统,其“基数”是2而不是10。这是最简单的数字系统,它只需要0和1两个数字,“0”用来表示“关”而“1”则用来表示“开”。
二进制系统对现代计算机是非常理想的数字系统,但在日常生活中使用则很不方便。如果用2替代变元,代数式会变成什么模样呢?我们以2x2+7为例,它应该成为2×22+7。然而,我们立刻遇到了麻烦,因为2与7都不是二进制系统中的数字!
二进制中只有0和1两个数字,那么2应该怎么写?答案是:10。在二进制中,10表示的数字等于1×21+ 0×20。简单地用口诀来记,可以说成“逢二进一”——这可以说是“二进制”这一称呼的由来。相似地,7等于22+21+20,即是以x= 2代入多项式x2+x+1的结果。所以在二进制记数方式中,7这个数字记成111。它不表示十进制的一百一十一,而是一个2的平方加上一个2再加上一个1。而207这个十进制数值若以二进制表示,则是11 001 111。很显然,在便利店的记账本里,这种冗长的记号远不如207简便,但二进制对现代计算机而言是最便捷的。
不到一百年前,二进制仍然被视为只有理论意义的数学古玩。突然之间,二进制因为计算机的发展变得必不可少,相关理论也因此极快地得到发展与完善。这是数学史上一遍遍重复着的故事:长期地看,没有任何数学是“无用的”。数论中大部分内容没有得到“实际”的应用,但这没有降低它的重要性,反而增强了它的魅力。没有人能够预言,哪一个看似冷僻的定理会突然间被引用,并且出乎意料地扮演起重要的角色。(www.chuimin.cn)
十六进制
我们说过,207的二进制表示是11001111。很显然,数字的二进制表示都很长,把它们写下来是很不方便的事情。然而,每四位二进制数字可以很方便地写成一位十六进制数,因此,计算机界经常使用十六进制数字来表示相应的二进制数。
十六进制的“个位数”有16种,阿拉伯数字不能满足需要,所以人们使用0,1,2,…,9,a,b,c,d,e,f来表示十六进制的所有“个位数字”。207为例,它的二进制表示的最后四位是1111,等于是十六进制的“f”,而前面剩下的是1100,十六进制表示为“c”。于是十进制数字207的十六进制表示就是“cf”。再如二进制数字10110,最后四位是6,前面的是1,所以它在十六进制中写成16。
需要注意,十六进制中的16表示的数值是:1×161+6×160,即十进制的22。同理,十六进制的cf表示12×161+ 15×160=207。
在有些城市的交通信号中,红灯秒数只用两位数表示。当红灯秒数超过100时,它的“十位数”往往就使用十六进制的数字。因此,如果你在南京看到红灯秒数显示为“c9”,千万别以为它出故障了,其实它很正常,表示的是129秒。
冯·诺伊曼
我们当前使用的计算机的结构,包括其内部采用的二进制编码方式,都是由大科学家冯·诺伊曼提出来的。冯·诺伊曼(1903—1957)原籍匈牙利,后移居美国。他在纯数学、应用数学以及计算机科学方面都做出了非常卓越的贡献。
冯·诺伊曼很喜欢在自己家里开派对。有一次,一位数学家同事要去冯·诺伊曼家参加派对,事先打电话问他家有没有什么好找的标志。冯·诺伊曼出门看了看自己的房子,回答说:有,我家房顶上站着一只鸽子。(最聪明的科学家,不动脑子时也是很糊涂的,回电话的冯·诺伊曼没有想到那鸽子可能很快飞走。)
我们随便写下一个数字,比如说:22。将这个数除以2,把结果写在它的下面。然后,再除以2。11除以2得到5以及余数1,我们将余数写在11的右边,而在11下面写下整数部分5。按照这个算法继续进行下去,直至最终得到1。整个过程如右图所示。
现在,我们将右边这列数字自下而上写出来,得到一个二进制数字10110。它恰好就是22的二进制表示。用这种方法我们总是可以求得一个十进制数的二进制表示,在往下阅读之前,您可以思考一下:为什么这是正确的算法?
如果您找到正确的切入点,这个问题就一点也不神秘。和很多的数学问题一样,一个问题只有在被恰当地提出时才能被正确地回答。在包括数学在内的许多研究领域里,很多人陷入困境是因为他给自己提出的问题是错误的,甚至是没有答案的。当别人对这个问题重新组织时,或者提出一个新的替代问题时,一切可能就迎刃而解了。
以上对计算一个数的二进制表示的步骤的描述,事实上将算法的原理隐藏起来了。我们先考虑一个更简单的、已经见过的例子:7=22+21+20,二进制表示即为111。我们从111的最右边开始考察。最右边的1意味着什么?它表示7这个数字包含1的奇数倍,因此它不在任何2的正数次方里。写下最末位这个1之后,需要表示的数就只是6而不是7。现在我们再看右起第二位数字——它也是1。这表达的含义是:6是21的奇数倍?正是如此!因此我们减去21,等于是说我们写下了1×21的简化形式,而余下的数等于4。接下来我们考虑4是22的奇数倍还是偶数倍?答案是1倍,这当然是奇数。因此,我们在22相应的位置写下1,然后再在原数中减去22。结果,我们完整地得到了7的二进制表示,即111。
另一方面,假设我们考虑的数值是9。首先,其二进制表示的最右边位置同样是1,因此我们从9中减去1,得到数值8。然而,8是21的偶数倍,因此在21的位置上应该是0而不是1。写下这个0,然后考虑下一个位置。需要表示成二进制的数值仍然是8,它又是22的偶数倍。所以,在22相应的位置我们还是写下0,而此时余下的数值同样是8。现在我们转而到了23的位置。由于8是23的奇数倍,因此我们在这个位置写下1,然后将8减去23。减法的结果是零,因此我们得到了9的二进制表示:1001。
现在来考察前述算例中的22。我们不理会其中的算法描述,特别是将余数写在右边的做法。相反地,我们提出问题:22是1的奇数倍还是偶数倍?答案是偶数倍。因此,22的二进制表示之末位是0。写下这个0,然后考虑22是21的奇数倍或偶数倍的问题。答案是奇数倍,因此我们在21位置上写下1,再从22中减去21——余下的数值是20。接下来,20是22的5倍即奇数倍,因此在22位置上写下1,并从20中减去22。现在,余下的数值——就是还没有表示成二进制的部分——等于16。16是23的偶数倍,因此我们在23的位置上写下0,然后考虑16与24的倍数关系。由于16恰好等于24,是一个奇数倍,因此24的位置上我们写下1。然后,我们就得到10110这个结果。这就是说,整个算法所得的是:
22=1×24+0×23+1×22+1×21+0×20。
贴合“二进制”这个术语,以上算法可以粗略地描述为:“逢二进一,余数留在当前的位置上”。细想的话我们可以发现,这种算法对其他进位制也是正确的。例如,假如我们想把十进制数207写成八进制数,那么我们也可以用同样的算法:207除以8得商数25以及余数7,将余数写在右边,商数写在下边;继续除以8,得商数3及余数1;由于3除以8只有余数3,因此我们得到207的八进制表示为:317。换句话说,我们得到的实质上是:
207=3×82+1×81+7×80。
有意思的是,在数十年前的埃塞俄比亚腹地的一个部落里,人们的乘法运算使用了与上述这种算法在数学上相通的做法,这是一个到埃塞俄比亚探险的军官的亲身经历,他在那里偶然买了七头牛。关于这次经历,这位军官在他的游记中写道:
我们去一个集市,想买七头牛。然而,虽然集市上有人卖牛,但卖牛者和我们的向导都不懂简单的算术,不知道七头牛的总价应该是多少钱。他们站在那里像是鸡同鸭讲,吵吵嚷嚷却得不到答案。最后他们叫来了当地的牧师,因为他是当地唯一能够解决这个算术问题的人。
牧师和他的儿子助手赶到后,在地上挖了一系列的小坑。这些坑的大小和茶杯大致相近,分成平行的两列。我们的翻译说,这些坑叫作“格子”。他们马上要做的涵盖了在这一地区进行交易所需要的所有数学,而所需要的则只是数数以及乘以和除以2的计算能力。
牧师儿子有满满一袋小石子。在第一列的第一个坑里,他放入7个小石子,每一个代表一头牛。第二列的第一个坑里则放入22个小石子,这是因为每头牛的价格是22。他们解释说,第一列坑的作用是作乘2计算:把第一个坑的石子数乘以2得到一个数目,将这个数目的石子放入第二个坑;然后再把第二个坑石子数目的两倍放入到第三坑……第一列坑就按照这个规律放置石子。而第二列坑则是用作除以2的计算——将上一个坑的石子数目除以2,商取整数,然后将此数目的石子放置到下一个坑里,直至商等于1为止。
现在,检查除法列石子数的奇偶。所有偶数都被看成是“坏”的,而奇数则是“好”的。除法列中出现“坏”的数目时,就把乘法列中对应坑里的石子移去。最后,把乘法列中所有剩下的石子数目相加,总数就是问题的答案。
写在纸上,这个牛价问题的算法如下:
这位军官验算了许多例子,发现通过这个乘法系列总能得到正确的结果。他感到很惊奇,因为他不明白这究竟是什么数学道理。事实上,如果我们将乘法列余下的数值提出公因子7,我们就会发现剩下的数字依次是2、4、16。而回想我们刚刚得到22的二进制表示等于10110,事情一下子就清楚了:牧师最后所做的加法确实相当于计算了7×22=154。
古埃及人的乘法
古埃及人用加法和加倍来做一般的乘法运算。例如,计算29乘以13时,他们会做一个列表,在第一左侧写1,右侧写13,然后将这一行加倍作为第二行,接着把第二行加倍作为第三行,如此继续,直到16倍为止:
然后,他们选择左侧数字相加等于29的行,将这些行右侧的数字相加,从而得到29乘以13的结果。
事实上,这种做法与二进制有相当紧密的联系。
民间流传着一个有趣的“猜数字”游戏,这个游戏使用如下的四张卡片:
游戏的玩法是:你让别人在心里选定一个0到15之间的整数,并告诉你这个数总共在哪些卡片里出现,然后你“猜”他选定的数字。而你的“猜”法很简单——只要将相应卡片里的第一个数加起来,就可以得出这人心里选定的那个数。
举个例子说,假设我在心里选定13这个数,告诉你它出现在第一、三、四张卡片上。你则把这三张卡片的第一个数相加,1+4+8=13,然后告诉我说:“我知道了,你心里选中的数是13。”
这个游戏虽然简单却也有趣,所谓的“猜”其实是计算。很多人都见过这个游戏,但却未必明了其背后的数学道理。是的,其背后是二进制。
第一张卡片中是1到15之间所有除以2余1的数,即二进制表示为“×××1”的数,而其第一个数是0001。相似地,第二张卡片中是1到15之间所有二进制表示为“××1×”的数,而其第一个数是0010。后两张依此类推。
如果某人心里选定的数之二进制表示为a4a3a2a1,则根据卡片的设计方式,当ai等于1时这个数即出现在第i张卡片上。由于a4a3a2a1=a4·1000+a3·0100+a2·0010+a1·0001,可知这个数恰等于它所出现的卡片上的第一个数之和。再以13为例,13这个数的二进制表示是1101,因此它在第一、三、四张卡片里有,而且其数值恰好等于0001+ 0100+1000。
简单而有趣,是不是?事实上,在明白了其中的原理之后,我们还可以利用其他进位制来制作卡片,设计相似而貌似高深的小游戏。例如,读者可以设计六张卡片,利用三进制创造一个0到26之间的“猜数字”游戏。
我小时候见过舅舅们玩一种“取火柴”的二人游戏,具体的玩法是:摆上三堆火柴,每堆火柴的数目随机。参加游戏的两个人轮流取走至少一根火柴,但每次只能任意从一个堆中拿取。游戏的胜负以谁取走最后一根火柴来决定——谁取走最后一根火柴算谁输。也就是说,游戏者的目标是让对方无路可走,不得不取走最后一根火柴。
这个游戏有一个最佳策略。面对一个不懂得这个策略的人,懂得的人必然可以取胜。如果游戏双方都懂得这个策略,那么游戏的胜负在火柴数目确定时就已无法改变。
有趣的是,这个最佳策略的分析依赖于二进制系统。如果我们习惯于以2为基数的计数系统,这个游戏就会变得很简单了。
全面的策略分析有些复杂,但简而言之,你取胜的策略是以“平衡”的状态挑战对手,迫使他打破平衡。然后你继续创造平衡,直至到达3-2-1或2-2-0或1-1-1三种简单情形。面对这些情形的对手是必败无疑的。
所谓“平衡”状态是所有2的次方数都成对的情形。例如,假设一开始三个堆的数目分别是19,31和25。写成2的次方和,即为:
三堆火柴结合起来看,除了多出一个16、一个4以及一个1之外,其他2的次方数都成对出现。因此我们面对这种局面时,应该从31根火柴的那堆中一次性取走21根火柴。这样,我们就给对手制造了19-10-25这样一个平衡局面,而对手就注定要失败了。继续上例,假设此时对手从19根火柴中取走15根,则此时你面对的是4-10-25:
现在,16,4,2,1都没有能够配对,并且分散在三个火柴堆里,我们怎么制造出新的平衡局面呢?显然,16是肯定无法配对的,所以我们必须从25中取走火柴。这样一想,问题变得简单起来——我们在25根火柴中留下与4,8,2配对的火柴数,即取走11根火柴,就可以形成4-10-14的平衡局面。再假如对手接下来取走第二堆中所有的七根火柴,那么我们的应对办法就是从14根中也取走七根,继续形成一个4-3-7的平衡的局面——注意:按照二进制表示,4-3-1不是平衡局面,我们千万不要错误地让自己陷入这种必败的情形。我们只有不断地制造平衡局面,才能够制造出上述那三种对手必败的简单情形。
在火柴成为人们随身物品的年代,它经常成为闲暇时小游戏的道具,“火柴游戏”曾经相当流行。我们前面既讲到罗马数字,又讲到了火柴,因此本章的最后,我们来看一个趣味故事——
在1893年美国西部的一个酒吧里,一个叫约翰的男子在桌子上用火柴摆出了如下的罗马数字算式:
然后他挑战在场的所有酒客,问最少移动多少根火柴,可以使之成为一个正确的等式?他以一美元的赌注赌别人说不出正确的答案。
不少聪明人纷纷拿出一美元放到桌上参赌,他们异口同声地说:很简单,把被加数里的1移动到右边,成为
两边就相等了。只移动了一根火柴,难道不是“最少”?
不料,约翰把参赌的酒客领到桌子的另一边,说:你们看,这个式子其实一根火柴都不需要移动。于是,在聪明人们目瞪口呆之际,约翰笑嘻嘻地收走了桌上的赌资。
这个故事所讲的并不是一个脑筋急转弯问题,它其实提醒我们:看问题可以有不同的角度。
掐指一算
我国的算命先生常会“掐指一算”,那就是使用手掌进行十二进制运算的过程。中国古代在天文与历法等方面使用十天干和十二地支,因此,中华文明虽以十进制为主,事实上也兼用十二进制和六十进制。
左手“掐指”,可以表示1到12,配合右手的五个手指,就可以表示所有六十进制的数字。不过,两河文明与我国传统的“掐指”方法是不一样的,它们都是用拇指“掐”(指点)其余四个手指的特定部分,但所“掐”的位置有所不同,具体情形如下:
如上所示,两河文明所用的位置是整个“指节”,而中华文明所用的则是指节之间的“点”。西方人用具体的“区域”而中国人用抽象的“点”,国际象棋与中国象棋之间同样体现出这种区别。
有关如数加珍:数字丛林的冒险之旅的文章

前文的分析同时告诉我们,完全平方数的数列中也没有两个项的比例等于2与3之外的任何其他素数,因此素数的平方根都是无理数。此外,虽然6不是素数,一个完全平方数也不会是另一个完全平方数的6倍,因此也是无理数。总之等等都是无理数。实数中有很多很多的无理数,这些无理数中“绝大部分”不是代数数,它们不能表示成任何代数方程的根,我们将这类数称为“超越数”。......
2023-10-30

在这里,找出数对的方法是用连分数展开,它本质上和辗转相除法等价。如果用连分数的想法,我们只要将77/34的连分数展开再额外进行一步就可以了。虽然我们总是可以把有限的连分数展开式逐步化简成单个分数p/ q,但任何无理数显然都不可以写成有限的连分数展开式。我们下面来考察某些无理数的连分数展开。但是,为了显得有点儿个性,我们要先把放在一边,先来考察的连分数展开。......
2023-10-30

包括原来的数在内,重新排列的数之第一个数字有9种选择。第二个数字的选取在第一个已经选定之后,因此总共有8种选择。在各种数学家排行榜中,高斯通常都名列前三位。高斯总结了复数的应用,严格证明了代数基本定理。在24岁时,高斯用他的数学知识,计算出了小行星谷神星的运行轨迹,轰动了整个天文学界。高斯知道他很多数学思想超越时代,很可能不会被时代所接受,因此他将很多研究结果留在自己的文稿里,而不向外界公开。......
2023-10-30

1726年,《格列佛游记》在英国首次出版便受到读者追捧,一周之内售空。第四次,格列佛因遭到叛变而走遍了慧国。我相信只要儿子翻开《格列佛游记》,就不会拒绝看下去。我去书店买来了《格列佛游记》,自己先看起来。儿子一回家,就会看到我手捧《格列佛游记》,津津有味地读着。两天后,我看完了《格列佛游记》,把书放在了他的床头。儿子被我引了过来,也开始看起了电影《格列佛游记》。......
2023-07-19

两位数的平方可以是四位数,这些数中没有一个满足上述这种神奇的逆序形式,但是其中有一对数也相当神奇:332=1089,992=9801。虽然四位的完全平方数没有对应的平方逆序数,它们中却另有别样的神奇:其中有连续五个四位平方数,它们的前半部分组成的两位数与后半部分组成的两位数的和也是完全平方数!除了以上所得到的长串连续自然数之外,还有其他一些折半和为完全平方的自然数。......
2023-10-30

可以想象,人生最大的悲剧莫过于在伯利兹迷失方向。2伯利兹城:伯利兹最大的城市、旧都,位于伯利兹河河口,加勒比海沿海,是伯利兹最重要的港口、金融和工业重镇。3大蓝洞:世界上最大的水下洞穴,位于伯利兹外海约97千米处。4安宝岛:伯利兹东北部加勒比海沿岸最大的岛屿,从南到北长约40千米,没有任何人工雕琢的纯自然海滩,拥有细腻的白色沙滩、清澈碧绿的海水,明媚的阳光和玛雅人居住过的古老小镇。......
2023-12-02

方法把和111相乘的乘数写在纸上,中间和前后留出适当的空格。即结果为13691295进位后为1370 295所以12345×111=1370295注意同样,更多位数乘以111的结果也都可以用相应的简单计算法计算,大家可以自己试着推算一下相应的公式。......
2023-10-27

我们在前面的章节里已经多次谈到过无穷数列和无穷级数,这一章,我们将作进一步了解——先稍稍正式地说一下它们的意思,然后讲几个有意思的例子。13世纪的数学家,意大利比萨城的列昂纳多另有一个名字叫作斐波那契,这个数列就是以他的名字命名的,称为“斐波那契数列”。因此,这个等式告诉我们,斐波那契数列的第n项是[n/2]+ 1个二项式系数的和,这些二项式系数在杨辉三角中处在一条上升的斜线上。......
2023-10-30
相关推荐