（001）3A级及以上景区总量增加量=3A级及以上景区总量×3A级及以上景区总量增长率Units：个/年（002）3A级及以上景区增长率=0.174 413Units：Fraction/Year（003）3A级及以上景区总量密度潜力=SQRT（人均3A级及以上景区总量密度×人均3A级及以上景区权重/人均3A级及以上景区总量标准）×（人均3A级及以上景区总量密度×人均3A级及以上景区总量权重/人均3......
2023-10-29
城市旅游环境承载力评价与优化研究：NSGA-Ⅱ算法解决方案
【摘要】：城市旅游环境承载力的优化是在旅游环境可持续利用的前提下，考虑旅游目的地经济效益、社会效益、环境效益的协调，得到合理的旅游环境承载力方案。根据NSGA-Ⅱ算法对旅游环境承载力优化模型求解，得出Pareto解集，为决策者提供参考。步骤4：检验是否满足终止条件，不满足则转步骤2，输出满足旅游环境承载力优化模型的Pareto解集。
城市旅游环境承载力的优化是在旅游环境可持续利用的前提下，考虑旅游目的地经济效益、社会效益、环境效益的协调，得到合理的旅游环境承载力方案。2002年，Deb等学者对NSGA提出改进，提出带精英保留策略的快速非支配排序遗传算法（NSGA-Ⅱ），NSGA-Ⅱ算法是目前最优秀的多目标优化算法之一，与NAGA算法相比，其在分布性与收敛性上更具优势，被国内外学者广泛关注。NSGA-Ⅱ算法的特点如下：第一，在目标函数个数是ξ、种群N中拥有的个体为ω的情况下，通过新的分级的快速非支配解的排序，将计算的复杂程度从O(ξN3)降维到O(ξN2)；第二，通过快速非支配解的排序，根据同级中各元素的适应度值，进行Pareto前沿面的扩展，为保证解尽可能地均匀分布，NSGA-Ⅱ采用拥挤距离替代NSGA算法中涉及的适值度共享方法，针对拥挤距离时间的复杂程度为O(ξ(2ω )log(2(ξ)))；第三，精英策略有助于扩大采样空间，促进父代和子代的结合，促使优良的下一代产生，达到提高结果精度的目的，通过对种群中的个体的分层存放提高种群水平。
6.3.4.1 初始化操作
初始化过程即针对旅游环境需求的四大主体（国内旅游者、入境旅游者、城镇居民、乡村居民）的数量设定参数( x1,x2,x3,x4)，在其取值范围内随机地生成初始个体信息，为后续的操作提供初始种群。
6.3.4.2 构造非支配集
假定群体Pop的规模是N，将Pop根据个体之间的支配关系进行分类排序，将种群划分为互不相交的子群体，形成m个子集P 1，P2，…，Pm，每个子集代表一个非支配等级，得出∀i；i，j∈{1,2,…,4}且i≠j，Pi∩Pj=Ø；P1≻P2≻…≻Pm，其中：Pk的个体受到Pk的直接支配（k=1，2，…，m-1）。构造非支配集：
6.3.4.3 拥挤距离和拥挤距离的比较算子
拥挤距离比较算子有效地解决了需要指定共享参数维持种群多样性的弊端。在旅游环境承载力寻优过程中，为了确保种群的分布性与多样性，通过计算拥挤距离，进行个体支配关系的分析，在构建新种群时根据支配关系考虑个体的选择。
聚集密度小的个体拥挤距离大，针对产生的群体，保留优秀的且聚集密度小的个体[178]，计算拥挤距离P[i]distance，通常情况下，若目标函数为n个，则拥挤距离的计算如公式（6-31）所示。
群体中个体具有非支配等级irank拥挤距离P[i]distance，根据个体间的支配关系进行排序，界定为当irank≤jrank且di≥dj，则i≥j，表示为个体i优于个体j，如图6-2所示。
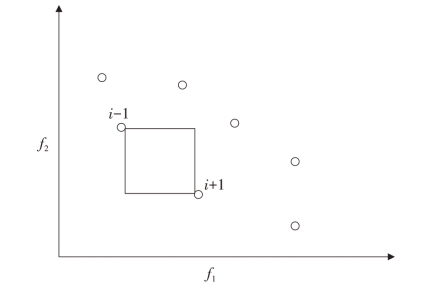
图6-2 拥挤距离
Fig.6-2 Crowding distance
根据旅游环境承载力优化目标Z1、Z2和Z3，则拥挤距离的计算如公式（6-31）所示。通常情况下，当子目标函数的个数r为3时，3个子目标进行排序的时间复杂性为O(3N log N)。
计算个体之间的拥挤距离为：
对初始化种群按优越程度即支配个数的多少进行非劣分层排序操作，并进行相应的拥挤度计算。(www.chuimin.cn)
6.3.4.4 Deb的MOEA
NSGA-Ⅱ根据偏序关系进行分类，设个体i和j为群体中的任意两个个体，其支配关系“≻n”如公式（6-32）所示。当两个个体非支配等级不同时，非支配等级（irank）低的个体具有优先权；如果非支配等级相同，拥挤距离大或拥挤密度小的优先考虑。
首先，P[i]distance算法寻优时首先产生一个初始群体P0，采用二元锦标赛通过个体的“选择、交叉和变异”产生新的群体Q0，二者的群体规模均为N，将Pt和Qt并入到Rt（初始t=0），根据Rt构造所有边界集，通过计算某个边界集中所有个体的拥挤距离，根据建立的偏序集，从中选出个体进入Pt+1，使得Pt+1的规模是N[179]。
根据NSGA-Ⅱ算法对旅游环境承载力优化模型求解，得出Pareto解集，为决策者提供参考。NSGA-Ⅱ算法仿真步骤为：
步骤1：对国内旅游者数量x1、国外旅游者数量x2、城镇人口数量x3、乡村人口数量x4采用实数编码方式，可以得到决策变量，以决策变量的取值范围为搜索空间。
步骤2：计算个体在目标函数Z1、Z2、Z3上的值。
步骤3：对旅游环境承载力模型进行优化，进化个体采用实数编码，遗传操作采用锦标赛选择、模拟二进制和多项式变异，且锦标赛选择的规模为2、交叉和变异的概率分别为0.9和0.1。判断由优化变量生成的目标参数是否满足设定要求。
步骤4：检验是否满足终止条件，不满足则转步骤2，输出满足旅游环境承载力优化模型的Pareto解集。
Ui(Z0(xi))为旅游环境系统约束下，经济效益、社会效益角度分析的隶属关系，当0≤σ≤1时，城市旅游环境承载力的目标函数Zi的隶属函数表述如公式（6-33）所示。
公式中：d0为目标函数Zi的最大期望值；d0-e0为目标函数Zi的最小期望值；θi为旅游收益值的不满意度/多主体的不满意程度。
考虑到城市旅游环境承载力影响因素的参数取值的分布存在不同形态，受不同分布的模糊数的隶属函数的影响，通过分析城市旅游环境承载力影响因素的潜在可提供量的扩张程度φ，鉴于φ∈[]0,1数值的不确定性，通过线性隶属关系描述隶属函数的增减关系。在多目标模型构建中，借助带参数的线性规划，界定影响因素选取适当参数值的模糊系数隶属关系的函数，通过模糊集的实函数，转化成规划问题。通过模型的构建，得出多主体在不同满意度下的期望值，界定隶属函数为：U()Zi=θi代表旅游环境需求的多主体的满意程度，随着θi取值的差异，得出核心主体之间的模糊最优决策，使核心主体之间达到需求的平衡，如图6-4所示。
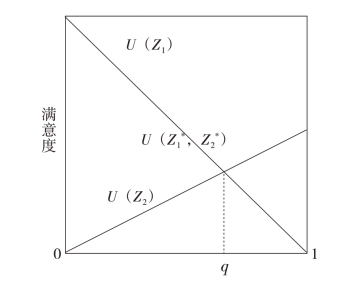
图6-4 满意度θi下的寻优过程
Fig.6-4 Optimization process under satisfaction θi
有关城市旅游环境承载力评价与优化研究的文章
- 详细阅读
-
城市旅游环境承载力的评价与优化研究详细阅读
本书针对旅游环境承载力的自然旅游环境承载力系统、经济旅游环境承载力系统、社会旅游环境承载力三大子系统，分析其相互作用，探讨子系统的耦合协调程度。图4-1旅游环境承载力子系统耦合协调发展作用机理 Fig.4-1The coupling coordination development interactive mechanism of tourism environment carrying capacity旅游环境承载力具有复杂性，涉及自然、经济、社会等多因素，反映了人类活动对旅游目的地资源利用程度与对旅游环境的干扰力度。......
2023-10-29
-
城市旅游环境承载力评价研究详细阅读
不同的利益相关者在旅游目的地发展中具有不同的主动性，根据相关研究成果，从“主动性、重要性和紧急性”三个角度进行分析，将多主体分为核心主体、蛰伏主体和边缘主体，其中核心主体对旅游发展施加主动影响，并且往往主动承担旅游发展的风险；蛰伏主体是那些被动承受旅游目的地发展带来负面影响的主体；边缘主体强调对旅游目的地发展影响不大，游离于旅游目的地利益相关者的边缘地带。......
2023-10-29
-
城市旅游环境承载力评价与优化研究成果详细阅读
鉴于利益相关者的动机、目标与核心利益等的差异，核心主体对旅游环境的需求必然经历反复的利益与权利博弈过程，使错综复杂的关系网络形成，核心主体利益的发展是其利益的博弈和行为协作的过程，导致相关主体资源的分配与利益格局的重新塑造。图3-8核心主体对旅游环境需求的帕累托改进与帕累托最优示意图 Fig.3-8Pareto improvement of core subjects’demand for tourism environment and Pareto’s best intentions......
2023-10-29
- 详细阅读
-
研究成果：城市旅游环境承载力评价与优化详细阅读
8.2.2.1拓展区的功能旅游目的地旅游环境承载力具有拓展能力，因此本书提出可浸性的概念，可浸性强调在旅游目的地范围内旅游环境系统的拓展、区域范围内旅游环境系统压力的转移，根据可浸区百分比状况，旅游环境系统的自我组织能力对其韧性起重要作用，要使旅游目的地在旅游高峰期具有韧性并能够自我组织以保持秩序，且能够保持健康，旅游目的地需要根据旅游目的地的特殊性对可浸性“向过去追溯”。......
2023-10-29
- 详细阅读
-
城市旅游环境承载力评价及优化详细阅读
在没有全面分析旅游环境需求多主体构成的情况下，最终得出来的承载力“数值”必定存在泡沫。在特定地域背景下，应注重旅游环境承载力指标体系的地域性，有针对性地构建指标体系，对旅游环境承载力进行系统研究，由初始的关照旅游者感知或满意水平，扩展到对当地居民为代表的利益主体的关照。......
2023-10-29
相关推荐