人工智能舞蹈交互系统实验结果与分析

针对要进行训练的动作样本库，我们在训练前做出了如下设置：两种类型的特征向量分别作为输入向量进行训练。在本书中，我们仅就基于C2a的参数设置的S-SOFM模型的训练结果进行探讨（见表2-1）。

表2-1 S-SOFM训练配置参数

在训练S-SOFM的过程中，我们构建了两个芭蕾舞动作库：其中一个库如表2-2所示，包含6个独立的动作（即G1-G6的每个动作都有单独的记录，独立于其他动作），每个动作都是由老师和学生分别做出的，学生的动作速度和肢体形态与老师的动作之间存在一定的差异（学生动作会用于测试）。此外，在表2-2中，我们还对每类动作进行了详细的描述，包含关键姿态、动作时长等，例如动作G1就是从第一个姿态变化到第二个姿态的舞蹈动作。图2-12详细地描绘了芭蕾舞中的6个基本造型。为了评估识别子系统对连续的舞蹈动作的在线识别能力，我们又创建了第二个动作数据库，见表2-3。在这个动作库中，我们收集了两个不同的组合舞蹈动作序列（D1和D2）。在实验中，我们把注意力集中在了D1上（所有的动作单元在我们的训练姿态空间中都有所表现）。

表2-2 动作库1

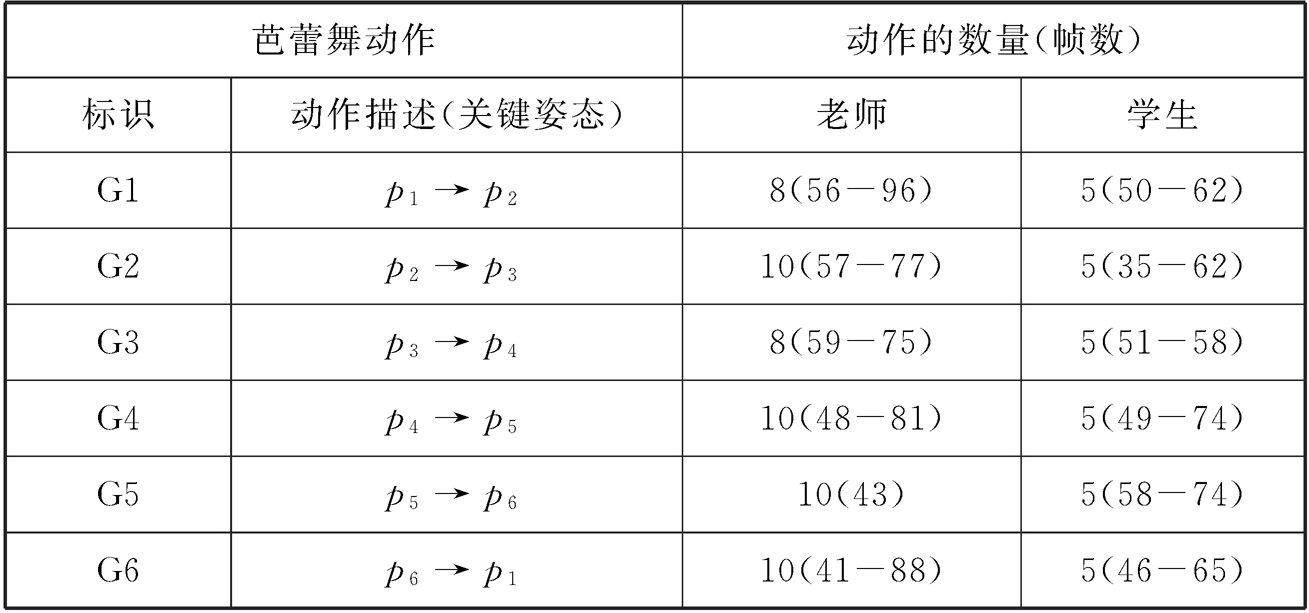
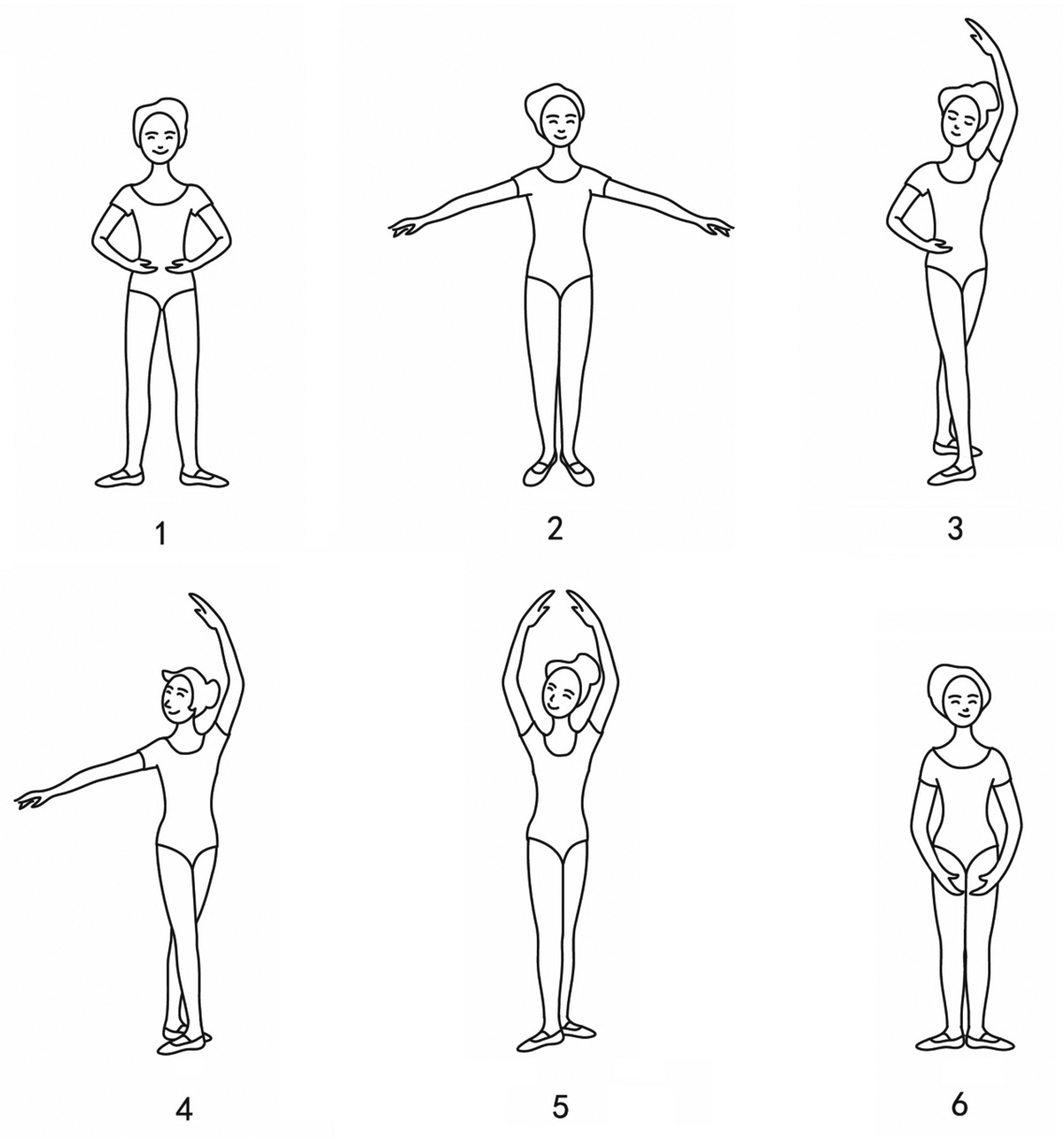
图2-12 芭蕾舞中的6个基本造型

表2-3 动作库2

在第一组实验中，我们将观察重复的动作（同样的动作内容，不同的动作序列）投射到S-SOFM模型中会产生什么样的变化。在图2-13中，每幅图都代表一个重复动作的映射效果，表示动作G11—G44在S-SOFM模型上的一系列映射结果。从图中可以直观地看到，每类动作在球体上所呈现的独特但相似度较高的轨迹。即使动作时长相差较大（在时长上的差异性高达40%），动作轨迹仍旧表现出一定的稳定性，这也体现了从姿态序列映射到姿态空间的一致性。轨迹上的实心标记分别代表动作的起点和动作的终点。由于不同类别的动作训练得到的路径具有自己的独特性，因此这些轨迹（动作）之间的高差异性有效地保证了动作识别效果。

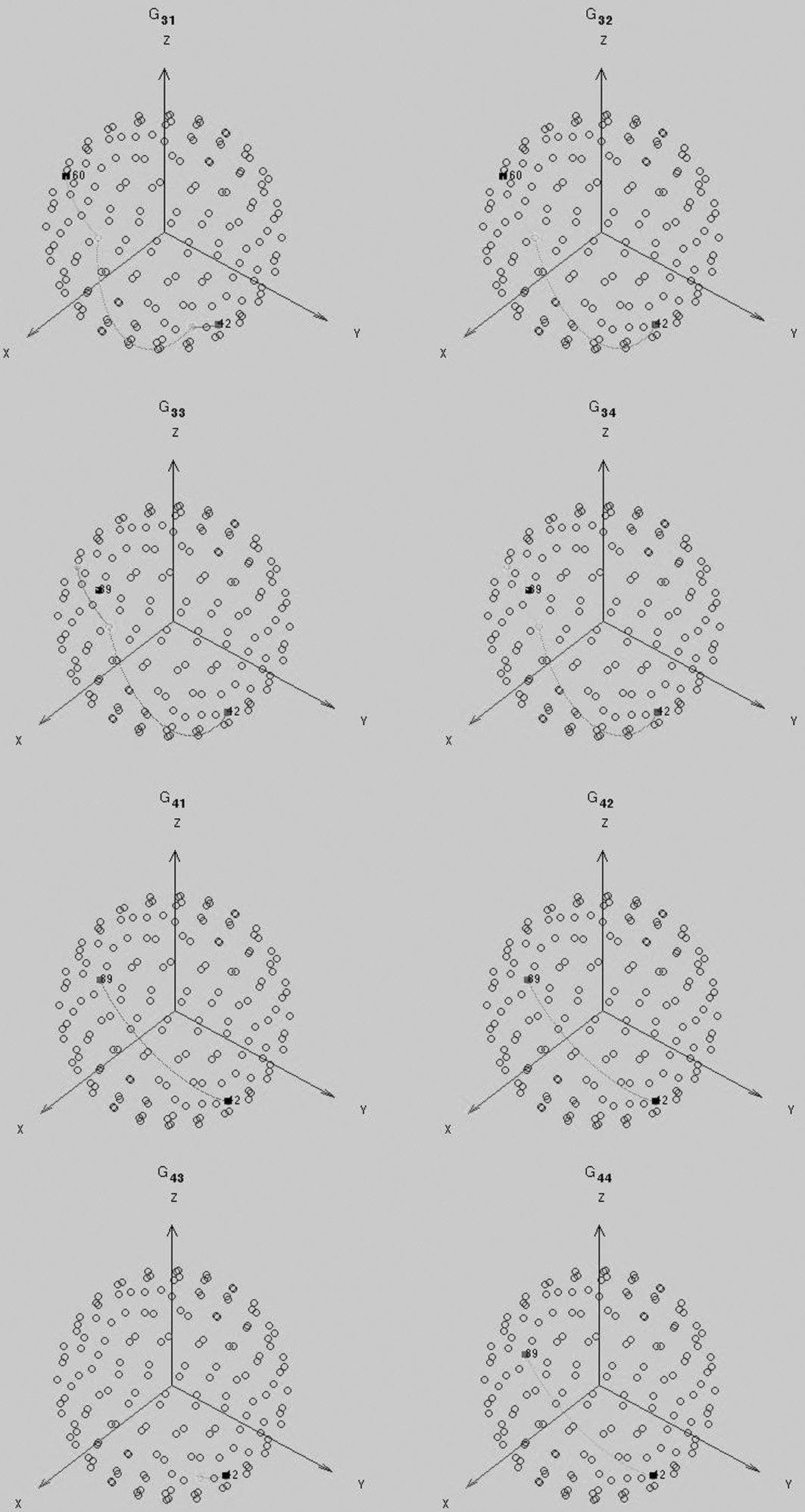
图2-13 G11—G44的动作轨迹

为评价我们所构建的S-SOFM输出空间的合理性，及动作模板和匹配标准的识别效果，我们利用动作数据库中的动作模板对基本舞蹈动作单元的识别进行第二组实验。在这个实验环节中，我们考虑了两个测试方案：第一个方案使用的训练样本与测试样本的比例为20%∶80%，第二个方案使用的比例为40%∶60%。换句话说，老师动作集合中的20%（也就是在每类动作中，从10个重复动作中选2个）被随机选中，用来作为动作模板，通过相似性度量法对剩下的80%参照样本进行识别判定。这个过程被重复了10次，并且我们对每个类别分类的准确度都进行了记录。这里的模板相似性通过以下3个距离来度量：L₁（绝对值距离）、L₂（欧式距离）和L₃（直方图相交距离）。

L₁距离的定义如下：

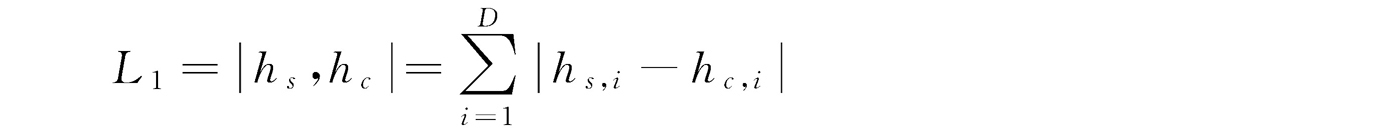
L₂距离的定义如下：

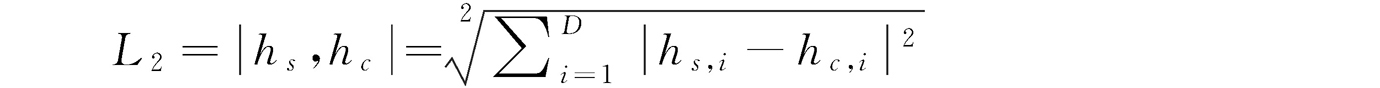
L₃距离的定义如下：

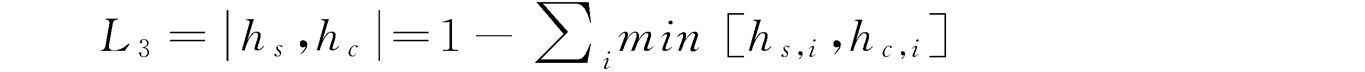
第二个实验方案的执行过程完全一样，只不过训练生成动作单元模板的动作集在动作库中的比例变为40%，而剩下的60%用来测试识别能力。基于不同的动作模板的实验结果见表2-4至表2-7。

表2-4 基于舞蹈姿态频率统计模板的识别率

表2-5 基于舞蹈姿态稀疏编码模板的识别率

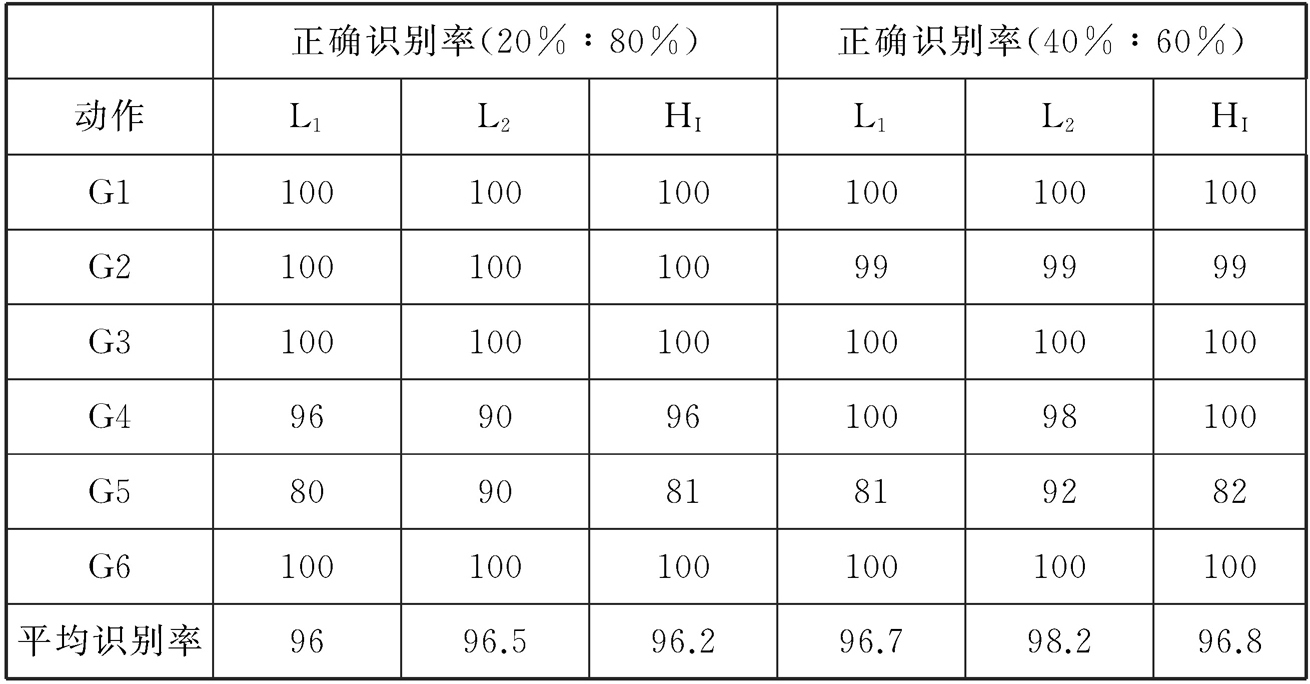
表2-6 基于舞蹈姿态转换矩阵模板的识别率

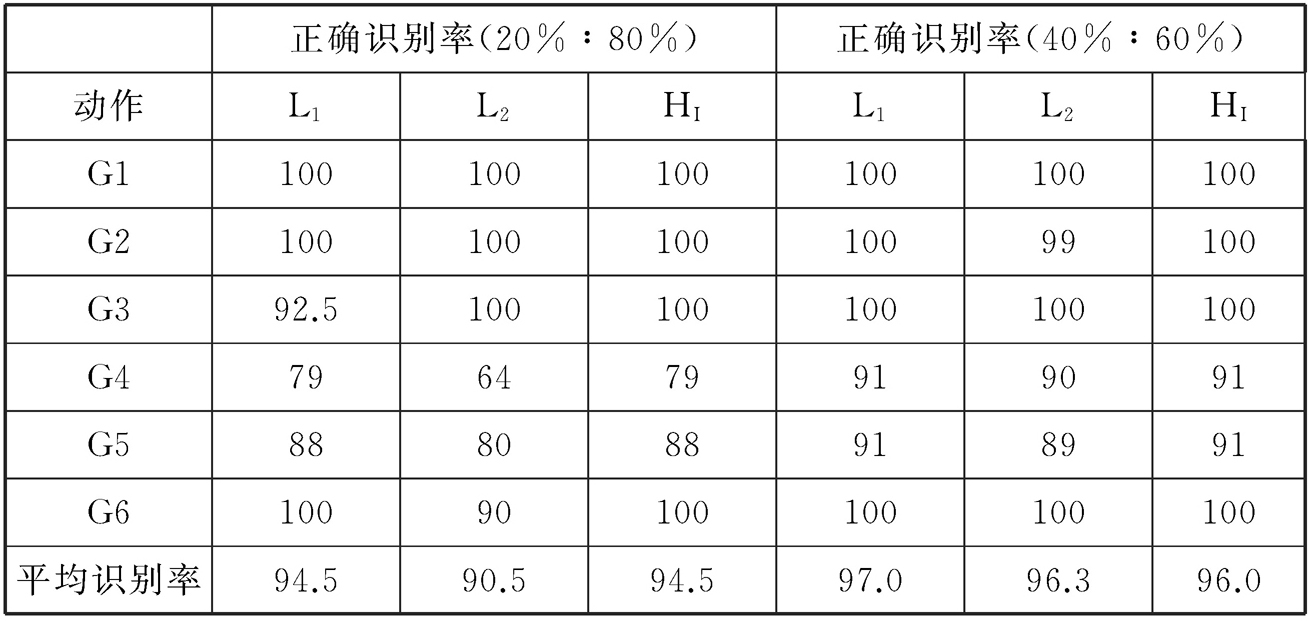
表2-7 基于舞蹈姿态转换矩阵稀疏编码模板的识别率

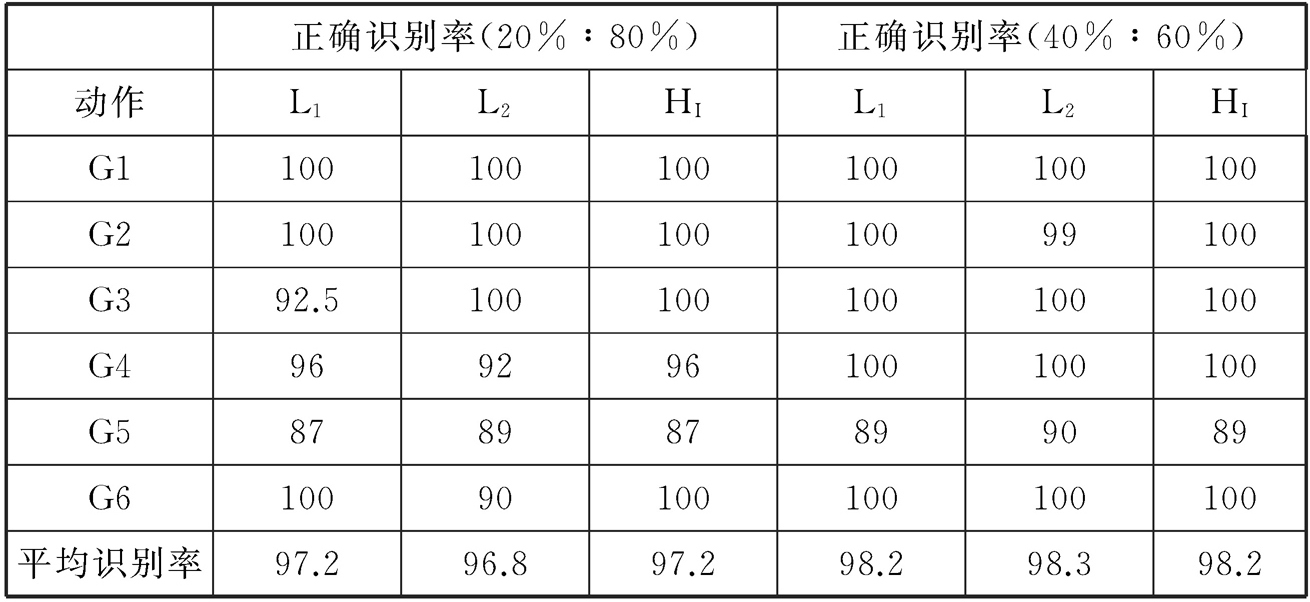
从表2-4到表2-7的数据中我们可以看出，由于动作相对简单，所以整体识别率都很高，这说明该方法对单动作检测有效，尤其是G1、G2、G3和G6四个舞蹈片段，它们的整体识别率相对较高。此外，从动作模板的构建方法上看，用稀疏编码构建的动作模板使用相似性度量方法会提升识别的效果，姿态转换矩阵稀疏编码整体表现最好。

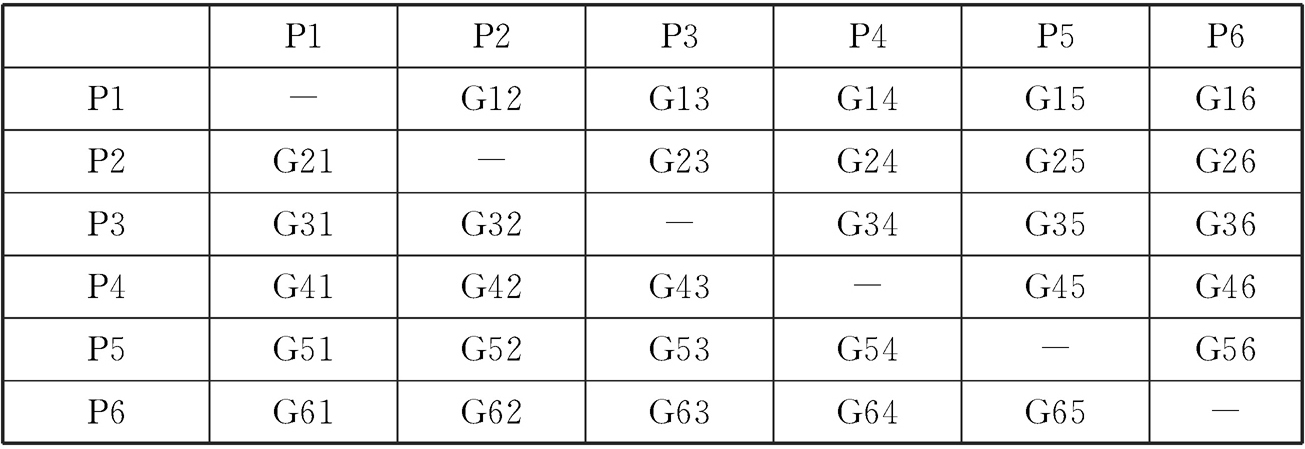
在第三组实验中，我们使用了更加丰富的舞蹈动作来评估我们所提出的识别方法。首先，我们定义了一个新的动作单元，它是由前面所介绍的基础关键姿态随机组合而成的。如表2-8所示，6个关键姿态构建了一组N个动作，其中，每个动作片段都是由其所对应的纵列的姿态和所对应的横列的姿态组合而成的，也就是说，动作G_ij表示该动作是从姿态P_i转换到姿态P_j的动作片段。

表2-8 30个动作的姿态构成

然后，基于上面的动作单元，我们构建了两个动作集合（如表2-9所示），集合1包含15个独立的动作，集合2包含和集合1的15个动作的关键姿态顺序相反的另外15个独立的动作，这样加在一起，总共30个动作。所有的舞蹈动作分别由老师、学生A、学生B来表演，每个动作执行10次，因此，一共有900个动作片段。

表2-9 动作集合1和动作集合2

(www.chuimin.cn)

我们先使用动作集合1。老师和学生A的动作会用于舞蹈动作的标准模板的构建和测试，而学生B的动作仅用于测试。因此，学生B的动作在进行系统训练的时候并不产生任何作用。为了评估S-SOFM模型的识别性能，系统按照（50%∶100%）的比例对样本进行训练。也就是说，从老师动作集合和学生A的动作集合中各随机选择50%的动作作为训练样本，以训练产生的结果作为被标识的动作模板，然后用其与其他输入动作进行相似性度量。

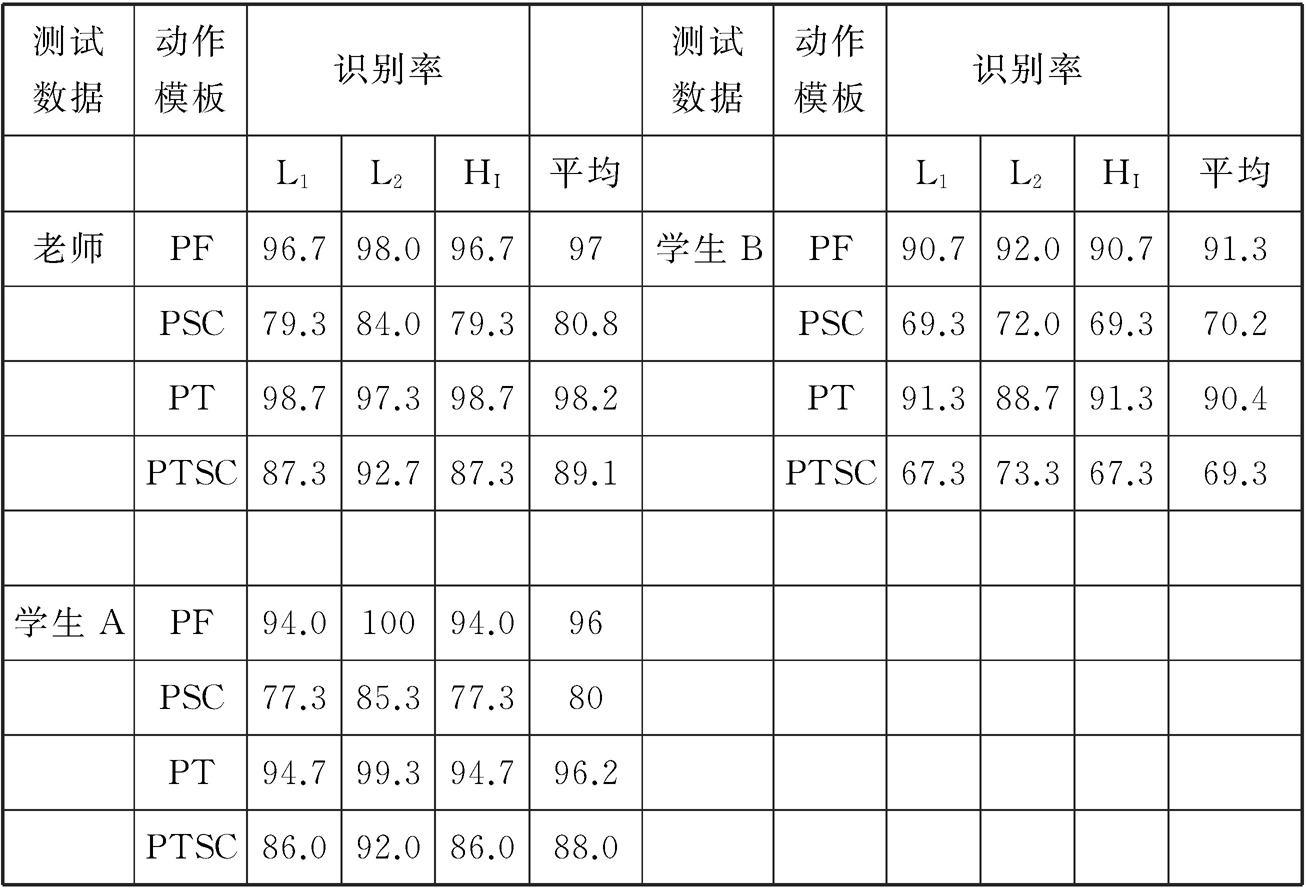
表2-10显示，对于更多种类的动作的识别效果，从整体上看，姿态频率统计（PF）动作模板和姿态转换矩阵（PT）动作模板的识别性能相对比较理想。当系统将姿态转换矩阵（PT）作为动作模板，把L₃直方图交叉距离作为相似性匹配准则，同时把姿态频率统计（PF）作为动作模板、L₂欧氏距离作为相似度匹配准则时，这两个方法的组合对于老师和学生A的动作识别率达到了98%。此外，使用学生B的舞蹈动作来做测试时，同样的组合的平均识别精确度高达92%，这表明训练系统在识别未知数据上具备泛化能力。

表2-10 第三组实验的识别率统计

在第四组实验中，我们加入了动作集合2，这样一共有30种动作。由于动作集合2所包含的15种动作都是动作集合1的反转动作，因此基于反转动作所构建的动作模板可能会和动作集合1所对应的动作模板存在一定的相似性，从而导致系统无法正确识别这两类动作。对于这类动作，我们可以从表2-11所示的实验结果中发现，当采用基于姿态转换矩阵（PT）的动作模板时，由于它保留了动作姿态的顺序，因此识别反转动作的优势明显。此外，从结果中我们还可以看出，通过姿态转换矩阵（PT）构建的动作模板的效果比其他的都好，老师动作的平均识别率为96%左右，不过学生动作的平均识别率降到了88%。这可能是因为学生表演的舞蹈序列前后不一致。

表2-11 第四组实验的识别率统计

为了评估系统使用贝叶斯后验概率估计算法识别连续动作的性能，在第五组测试实验中，我们使用了表2-3中的组合舞蹈动作片段D1。对于持续输入的动作片段，因时间不断累积而增长的舞蹈姿态序列被投射到S-SOFM模型上，生成了一个动态序列S_u。通过使用舞蹈姿态频率统计法和姿态转换矩阵模式，对老师和学生的舞蹈动作构建动作模板，然后基于这两个模板进行实时动态估算，从而得到一个不断更新的后验概率P（c|S_u），依据这个概率可以估算新舞蹈姿态属于动作类别c的概率。

图2-14和图 2-15表示的是对于老师的舞蹈动作，基于不同的动作描述模板所得到的后验概率曲线和在线识别率。从图中我们可以看出，使用这两个动作模板对连续动作进行动作识别，后验概率曲线和在线识别率表现得都很稳健。根据这个结果，系统能够针对动作片段D1以98.6%的准确率识别出老师的舞蹈动作。学生动作的识别结果也令人满意。学生和老师不一样，重复正确动作的能力有限，虽然有些小的数据损失，不过动作识别结果整体上符合实际情况（识别率为84.3%—89%，见图2-16、图2-17）。对于后验概率，在出现混淆的地方，该系统可能会在相对较短的时间内判定该动作为其他类别，然后再回到正确的选择。

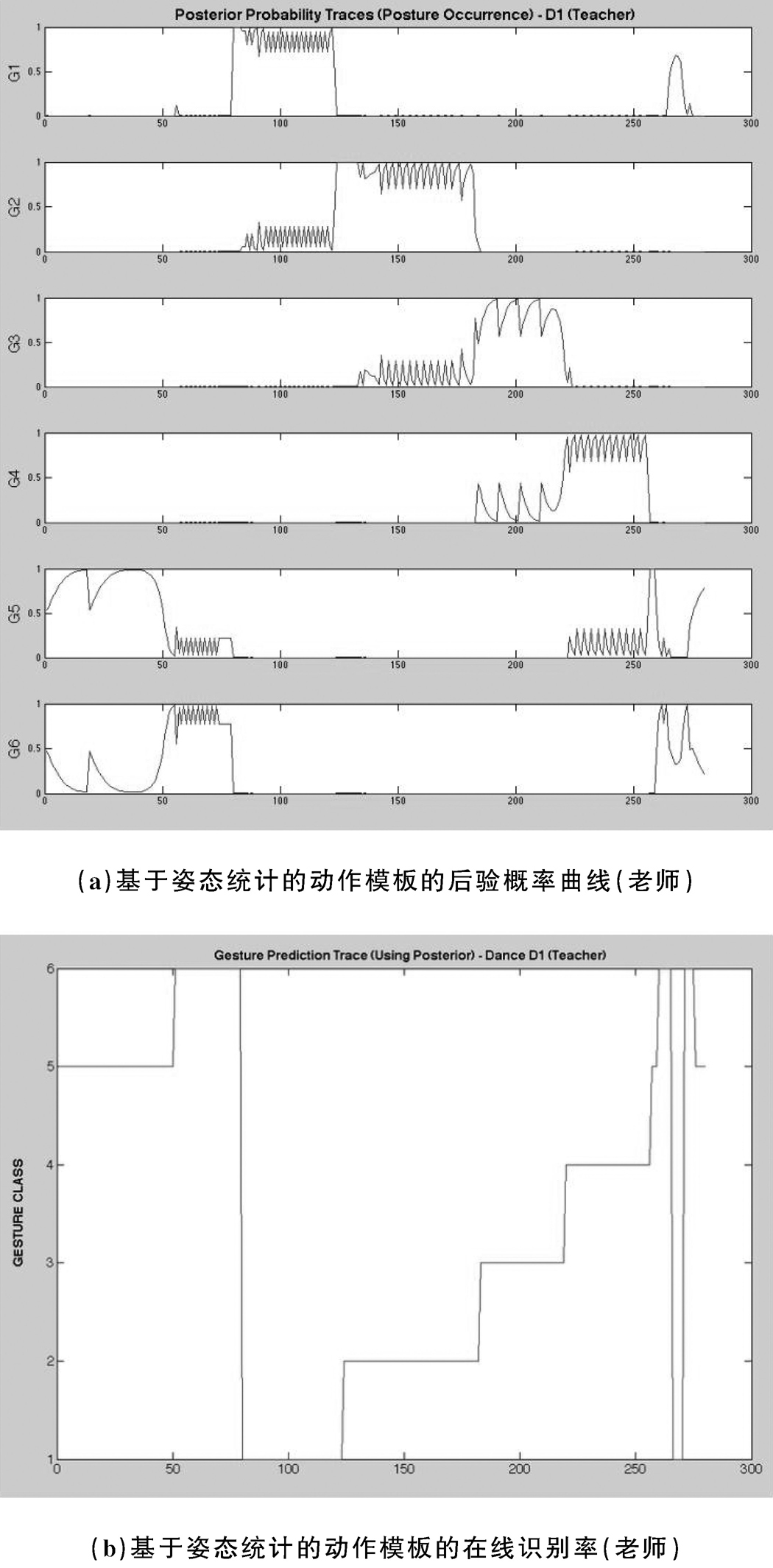
图2-14 基于姿态统计的动作模板的后验概率曲线和在线识别率（老师）

图2-15 基于姿态转换矩阵的动作模板的后验概率曲线和在线识别率（老师）

本章提出了一个新的舞蹈动作识别子系统，它可以较好地对学生的舞蹈动作进行识别。该系统基于前文提出的舞蹈特征提取方法，利用S-SOFM网络训练得到一个球形自组织特征映射模型，以此量化典型舞蹈动作中的姿势空间；然后通过把序列化的舞蹈姿势投射到S-SOFM输出空间中，得到一条平滑的轨迹，这就是一个动作的基本信息模板；最后，通过使用4个不同的动作模板对每类动作进行高层次描述，并且采用3种不同的算法对老师和学生的动作进行相似性评估。

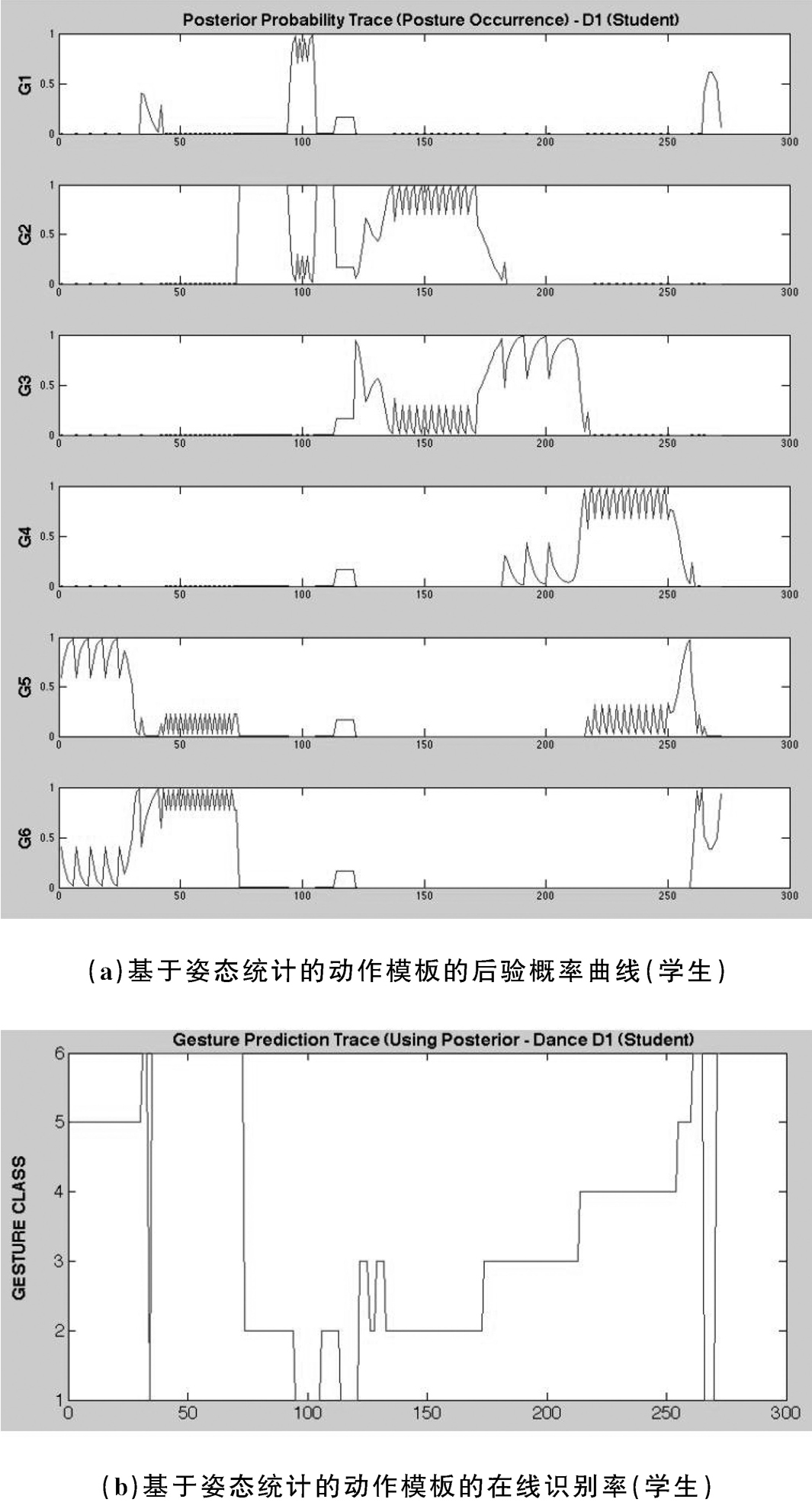
图2-16 基于姿态统计的动作模板的后验概率曲线和在线识别率（学生）

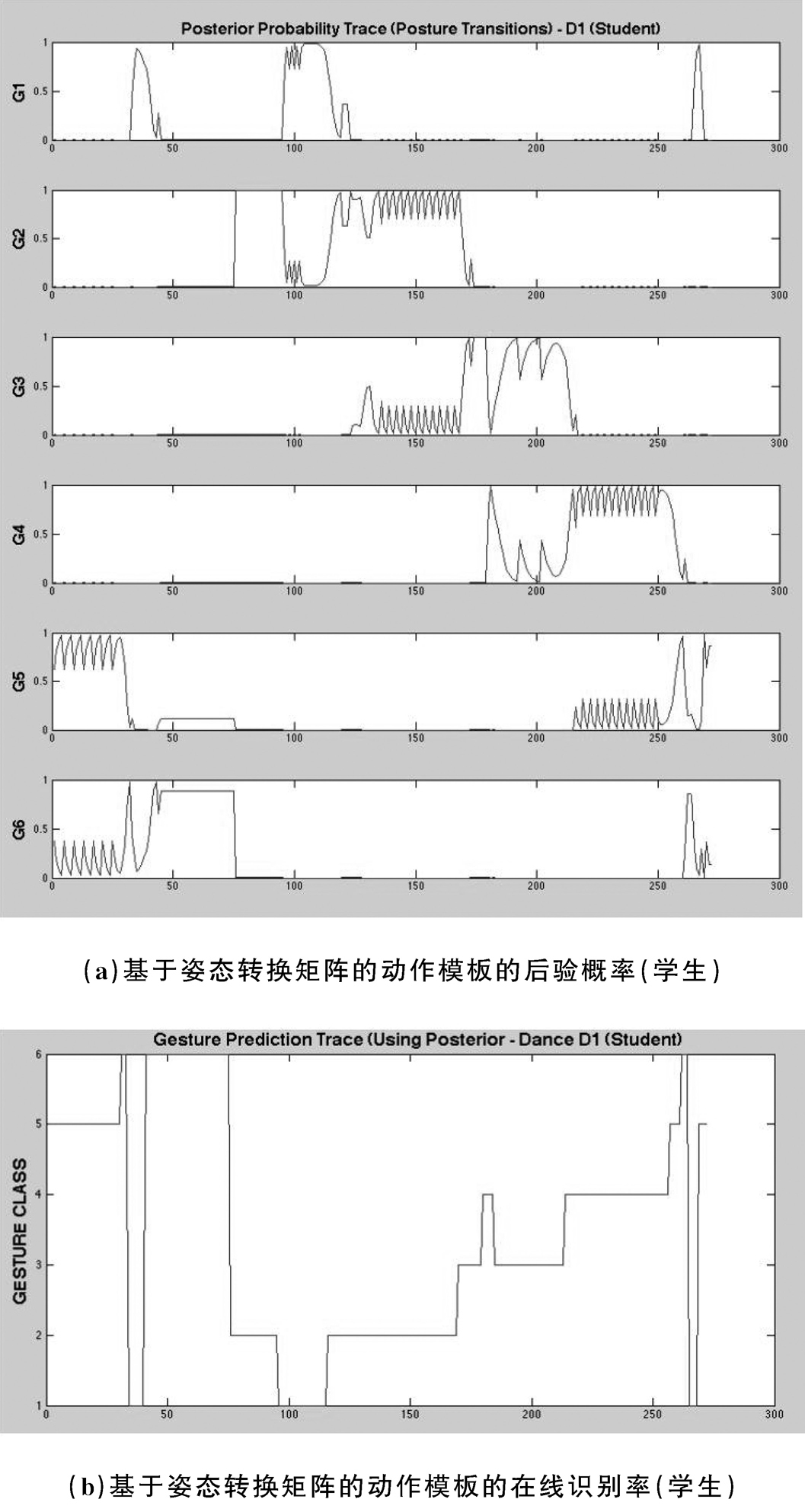
图2-17 基于姿态转换矩阵的动作模板的后验概率和在线识别率（学生）

该系统对于独立动作的识别率在90.5%—99.5%，识别的方法显示出较好的健壮性。考虑到动作的时间顺序，将姿态转换矩阵作为动作模板会使动作的识别率有显著提升。在识别连续动作的实验中，由于使用了贝叶斯后验概率估计算法（将直方图交叉距离作为相似性度量准则）对连续动作进行在线识别，因此系统对老师以及学生的舞蹈动作的识别率都比较理想。

[1] 冯百跃. 舞蹈训练学概论［M］. 上海：上海音乐出版社，2009：3.
闫洁. 舞蹈创作中的“造型性”与“流畅感”［J］.时代文学，2009（8）：180-181.
刘青戈. 现代舞蹈的身体语言［M］.上海：上海音乐出版社，2004.
于平. 舞蹈形态学 ［M］. 北京：北京舞蹈学院，1998.
吕艺生. 舞蹈美学［M］. 北京：中央民族出版社，2013.

[2] SALVADOR S，CHAN P.Toward accurate dynamic time warping in linear time and space［J］.Intelligent Data Analysis，2007，11（5）：561-580.

[3] ZHAO Q，WANG L H，IP H H S，et al. Human 3D motion recognition based on spatial-temporal context of joints［C］. 20th International Conference on Pattern Recognition，2010：2740-2743.
RAPTIS M，KIROVSKI D，HOPPE H. Real-time classification of dance gestures from skeleton animation［C］.Proceedings of the 2011 ACM SIGGRAPH/Eurographics Symposium on Computer Animation，2011：147-156.
LV F J，NEVATIA R. Recognition and segmentation of 3D human action using HMM and multi-class adaboost［C］.European Conference on Computer Vision，2006：359-372.

[4] 陈松乐，孙正兴，张岩，等. 民族舞蹈运动数据的实例检索方法［J］. 计算机辅助设计与图形学学报，2014，26（2）：198-210.

[5] KOHONEN T. The Self-organizing maps［J］. Proceedings of the IEEE，1990，78（9）：1464-1480.

[6] WU Y，TAKATSUKA M. Spherical self-organizing map using efficient indexed geodesic data structure［J］. Neural networks，2006，19（6）：900-910.
SANGOLE A，KNOPF G K. Visualization of randomly ordered numeric data sets using spherical self-organizing feature maps［J］. Computer & graphics，2003，27（6）：963-976.
SANGOLE A P，LEONTITSIS A.Spherical self-organizing feature map：an introductory review［J］. International journal of bifurcation and chaos，2006，16（11）：3195-3206.
CHIU C，CHAO S，WU M，et al. Content-base retrieval for human motion data［J］.Journal of visual communication and image representation，2004，15（3）：446-466

[7] 陈松乐，孙正兴，张岩，等. 民族舞蹈运动数据的实例检索方法［J］. 计算机辅助设计与图形学学报，2014，26（2）：198-210.

[8] WU S，XIA S，WANG Z，et al. Efficient motion data indexing and retrieval with local similarity measure of motion strings［J］.The visual computer，2009，25（5-7）：499-508.

[9] BOUDJEMAI F，ENBERG P B，POSTAIRE J G. Self organizing spherical map architecture for 3D object modeling［C］. Proceedings of workshop on self-organizing maps，2003.

[10] CHIU C，CHAO S，WU M，et al. Content-base retrieval for human motion data［J］.Journal of visual communication and image representation，2004，15（3）：446-466.

[11] WU Y，TAKATSUKA M. Spherical self-organizing map using efficient indexed geodesic data structure［J］. Neural networks，2006，19（6）：900-910.

[12] SANGOLE A，KNOPF G K. Visualization of randomly ordered numeric data sets using spherical self-organizing feature maps［J］. Computer & graphics，2003，27（6）：963-976.
SANGOLE A P，LEONTITSIS A.Spherical self-organizing feature map：an introductory review［J］. International journal of bifurcation and chaos，2006，16（11）：3195-3206.

[13] BOUDJEMAI F，ENBERG P B，POSTAIRE J G. Self organizing spherical map architecture for 3D object modeling［C］.Proceedings of workshop on self-organizing maps，2003.

[14] HIROKAZU N，ALTAF-U-A M D，KUROKAWA K，et al.Spherical SOM and arrangement of neurons using helix on sphere［J］.IPSJ digital courier，2006，2：133-137.

[15] SANGOLE A，KNOPF G K. Visualization of randomly ordered numeric data sets using spherical self-organizing feature maps［J］. Computer & graphics，2003，27（6）：963-976.
SANGOLE A P，LEONTITSIS A.Spherical self-organizing feature map：an introductory review［J］. International journal of bifurcation and chaos，2006，16（11）：3195-3206.

[16] KAWASHIMA M，SHIMADA A M，TANIGUCHI R-I. Early recognition of gesture patterns using sparse code of self-organising map［C］.Advances in Self-Organizing Maps，2009：116-123.
YOSHIMURA M，MINE N，KAI T，et al.Quantification of characteristic features of Japanese dance for individuality recognition［C］.IEEE International Workshop Robot and Human Interactive Communication，2001：193-199.

[17] KAWASHIMA M，SHIMADA A M，TANIGUCHI R-I. Early recognition of gesture patterns using sparse code of self-organising map［C］.Advances in Self-Organizing Maps，2009：116-123.
YOSHIMURA M，MINE N，KAI T，et al.Quantification of characteristic features of Japanese dance for individuality recognition［C］.IEEE International Workshop on Robot and Human Interactive Communication，2001：193-199.