SOFM和S-SOFM训练学习算法的实用指南

2023-10-29 理论教育版权反馈

【摘要】：自组织特征映射神经网络是由芬兰学者Kohonen在1982年提出的一种聚类学习方法。SOFM目前主要用于不同领域的高维数据的聚类、分类、抽样和可视化。图2-2 GeoSOFM的数据存储结构图2-3 显示了Sangole等人[12]构建的S-SOFM。在本书中，我们的工作主要是基于Sangole的S-SOFM工作成果，使邻居节点的管理方式和计算复杂度都能满足舞蹈姿态之间的强关联性。图2-4的流程图显示了S-SOFM的训练学习过程，该算法分为初始化、竞争、学习、重复迭代、得到获胜神经元等步骤。

自组织特征映射神经网络（Self-organizing Feature Map，SOFM）是由芬兰学者Kohonen在1982年提出的一种聚类学习方法。Kohonen在文章中把SOFM描述为 “一个高维数据的可视化和分析工具”^[5]。SOFM目前主要用于不同领域的高维数据的聚类、分类、抽样和可视化。^[6]SOFM属于竞争型自组织神经网络，是一种无监督的学习方法。^[7]与其他神经网络不同，它只有两层，分别是输入层和输出层（或被称为竞争层）。输入层的各神经元和输出层的各神经元之间是相连的，而传统的SOFM输出层是二维的。图2-1分别显示了传统输出层为一维线性分布和二维矩形排列分布的情况，其主要特点如下。

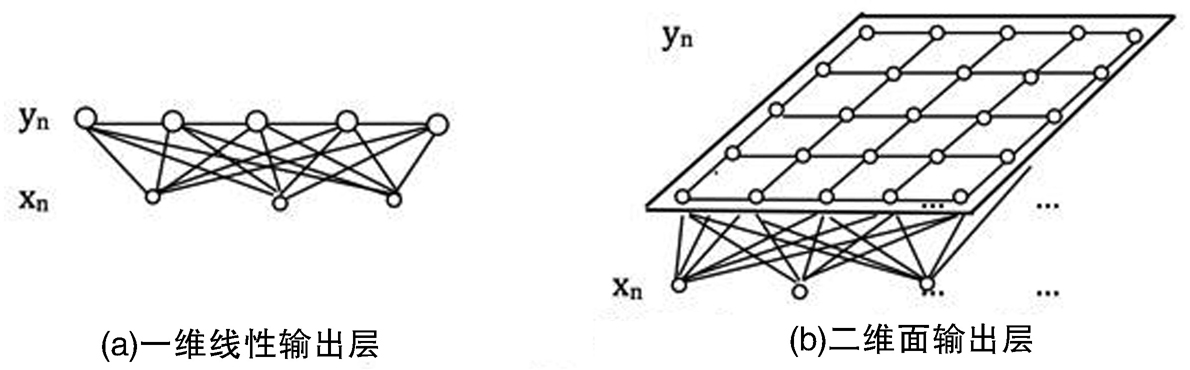
图2-1 SOFM 神经网络模型

（1）输入层的N维矢量数据将会映射到较低维度，对输入数据起到聚类、降维的作用。

（2）SOFM没有隐藏的输出神经元，输入数据的离散分布也会以同样规则的排列方式被映射到输出空间，也就是说，输出的神经元之间保留了原始数据之间的逻辑拓扑关系。

（3）不对输出分类的正确性或者“监督”进行评价，也就是说“没有指定明确的输出目标”^[8]。

（4）具有自组织概率性质，能根据样本出现在输入空间的概率密度，自组织地形成与输入空间概率分布相对应的神经元的空间密度关系。

然而，传统的平面SOFM具有“边界效应”这一缺点。^[9]在训练期间，神经元与其他单元竞争，获胜神经元及其“邻居”的权重将被更新，从而会对相似的数据区域进行建模。理想情况下，所有神经元都有平等的机会参与竞争，从而获得更新权重的机会。然而，在平面的输出层中，输出层边界处的单元拥有的邻居比平面内部单元少，在训练期间获得更新权重的机会无法和其内部的单元相同。因此，在训练结束时，边界处可能不会形成输入数据空间所期望的相似区域，从而导致“边界效应”。针对这种情况，研究者提出了优化的SOFM，如Kohonen从数据的角度，采用启发式加权规则法和局部线性平滑法对SOFM进行优化；还有学者提出将平面空间的边缘连接起来，形成无边缘的图形，例如球面或环面的SOFM，他们^[10]将球面和平面的计算复杂度进行比较，结果发现球体形状不仅与传统的SOFM模型运行得一样快，而且在更短的训练周期内更准确地表达了数据。基于球面的SOFM，目前存在如下拓扑结构：GeoSOFM、S-SOFM（Spherical Self-organizing Feature Map）和H-SOFM。GeoSOFM由Wu等人^[11]提出，如图2-2所示。他们采用二维矩形网格数据结构来存储二十面体的顶点数据，减少了维持栅格结构的计算开销，提高了顶点索引的速度，避免了在检索方面的性能损失。这种数据结构比较适合高维、可变的输出节点。

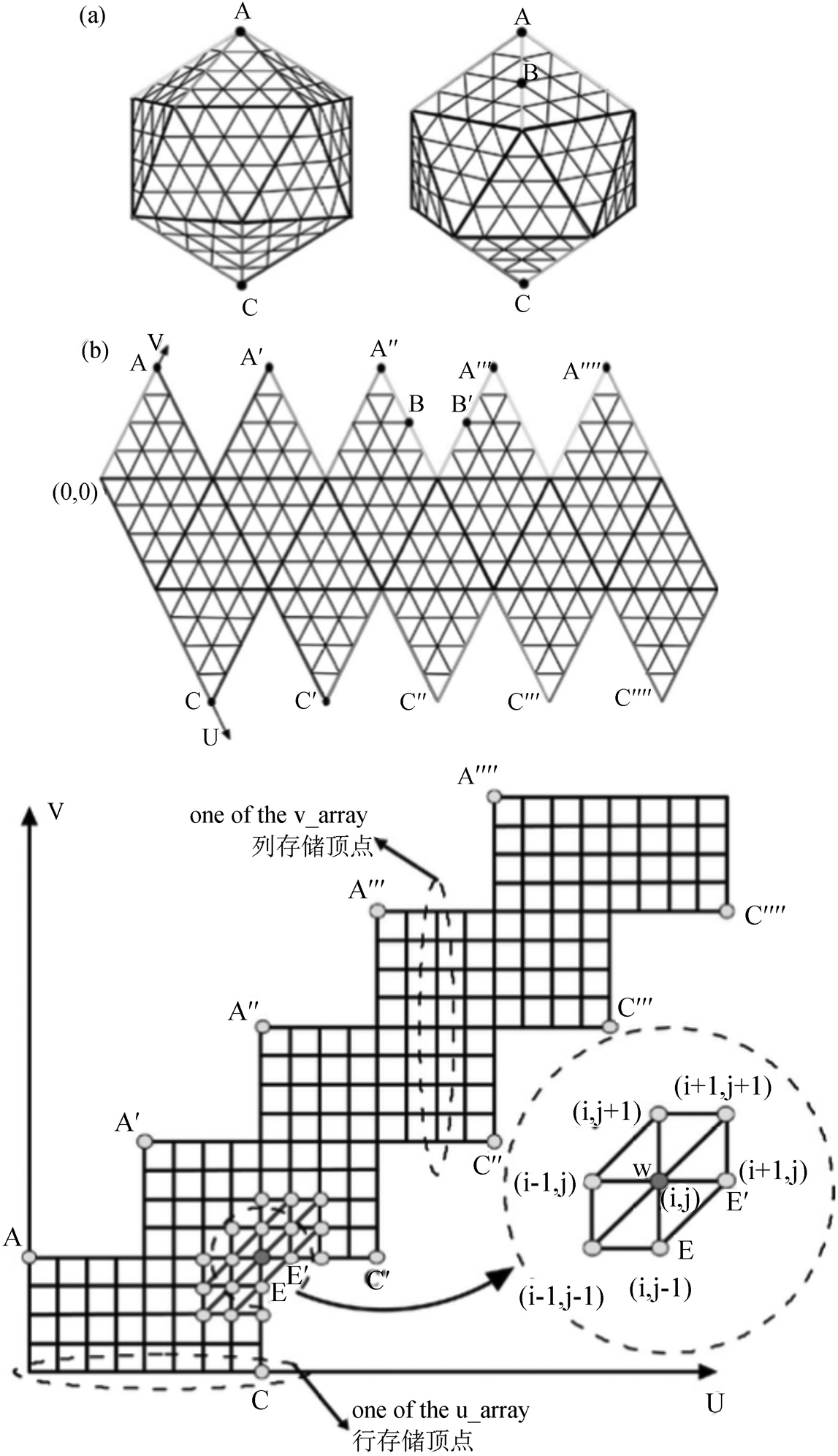
图2-2 GeoSOFM的数据存储结构

图2-3 显示了Sangole等人^[12]构建的S-SOFM。每个网格单元会存储一个由其直接“邻居”生成的列表，并尝试在三维沉浸式虚拟现实环境中与S-SOFM进行交互式数据分析。

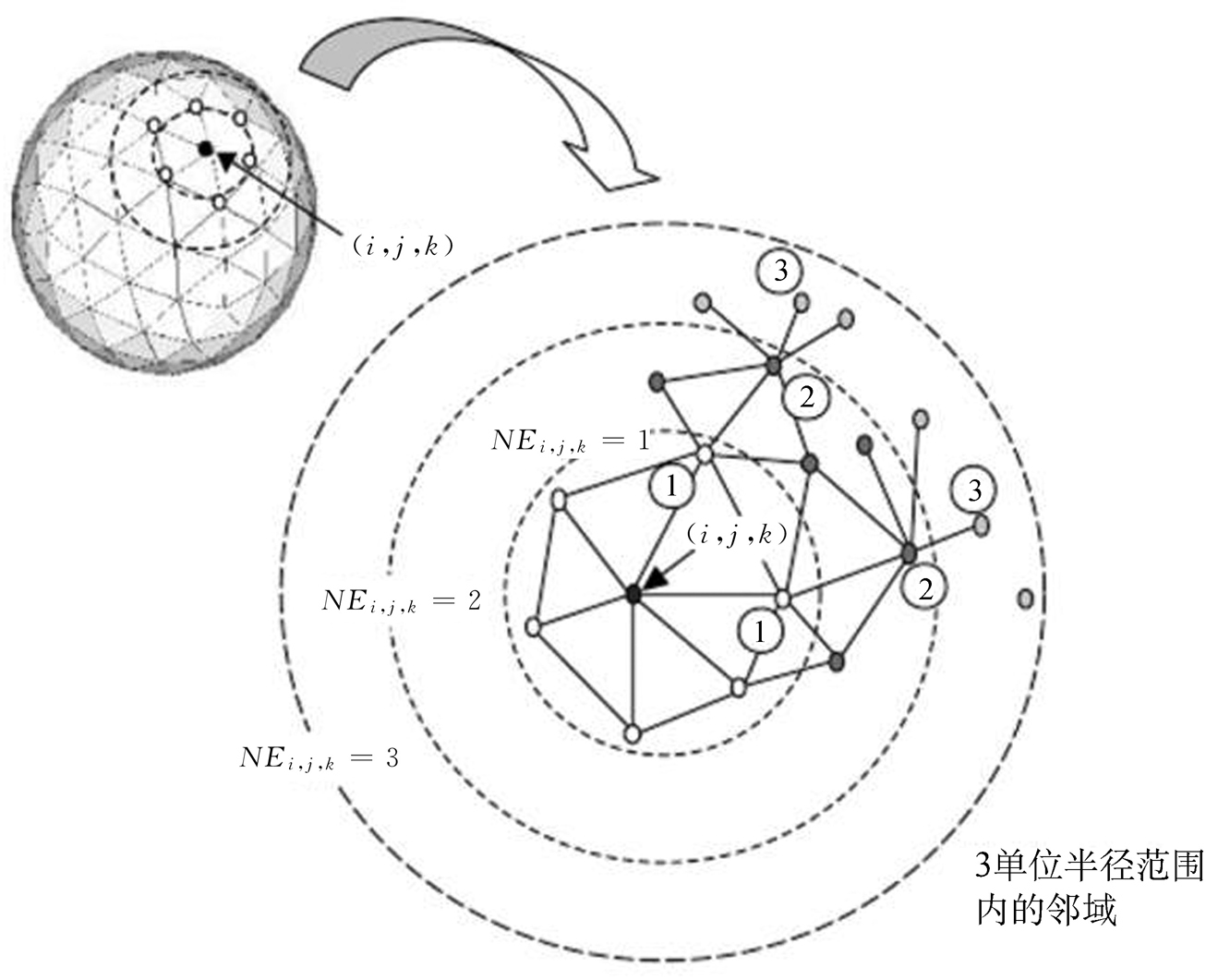
图2-3 S-SOFM结构

Boudjemai等人^[13]构建了3D-SOFM模型，其主要目的是通过构建3D模型实现数据的可视化。Hirokazu等人^[14]开发了H-SOFM沿螺旋排列神经元，把覆盖于球体表面的螺旋线分成相等的部分，并允许设定任意数量的神经元，不过在训练过程中，邻居节点的计算较复杂。在本书中，我们的工作主要是基于Sangole的S-SOFM工作成果，使邻居节点的管理方式和计算复杂度都能满足舞蹈姿态之间的强关联性。

(www.chuimin.cn)

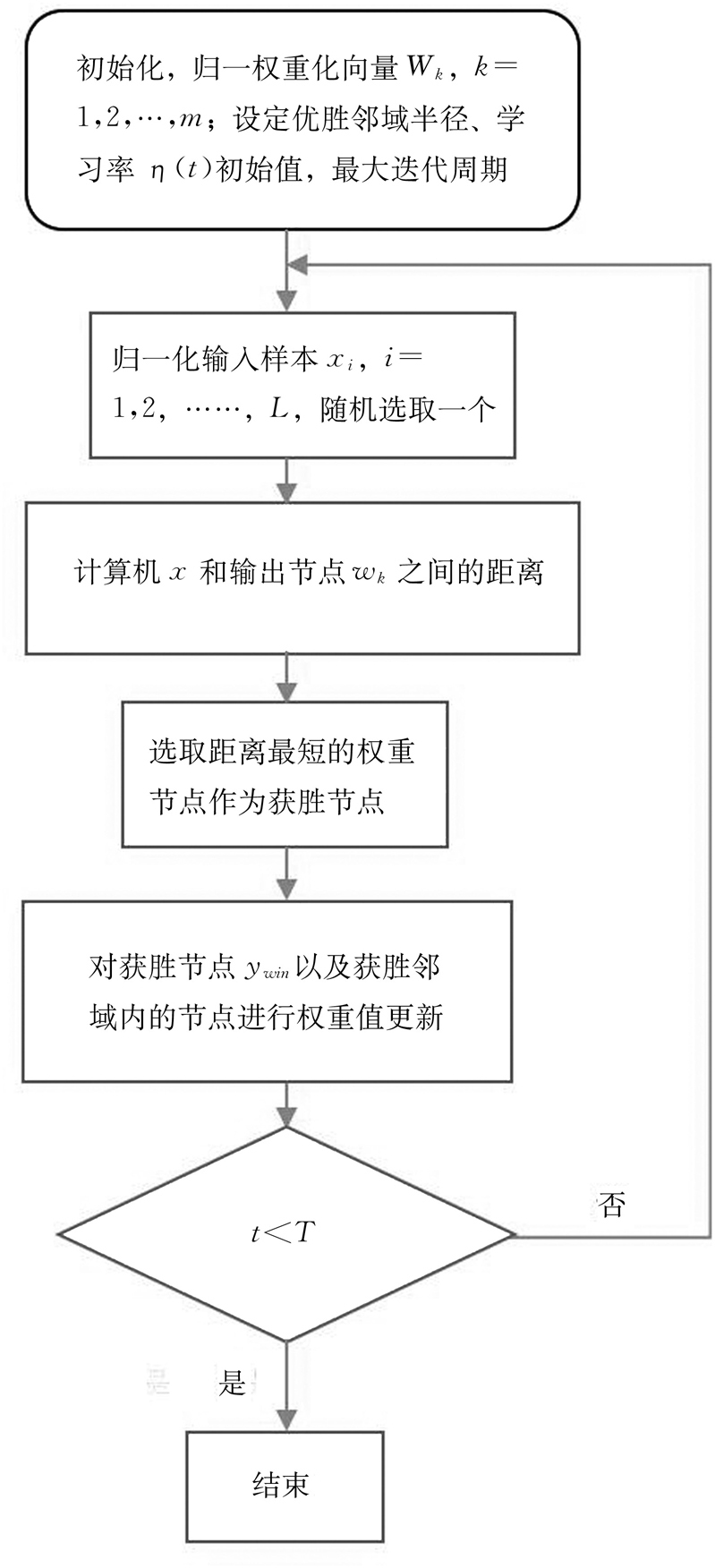
图2-4 S-SOFM算法过程

与2D的SOFM相比，S-SOFM继承了SOFM的优点：保持输入样本空间的拓扑结构不变，同时消除了“边界效应”；所有的神经元都有相等的几何区域，输入层特征空间中的密度区域在映射到S-SOFM之后具有相等间隔和以最大限度分离的对应节点位置；通过SOFM算法，对输入的样本在训练学习之后自动形成一种内部表达，最终将其映射到输出层中。如果以舞蹈动作为研究对象，那么输出层特征空间的建立实际上就是将已有的舞蹈动作作为训练样本，输入到S-SOFM空间中进行聚类的过程。最终可以在输出的球面空间中形成更易于识别的人体运动轨迹，通过识别这些轨迹，能有效地区分相对复杂的人体动作。此外，由于从球体中读取复杂的高维度信息更加直接、容易，因此S-SOFM具有更好的可视化效果，聚类后的结果可以通过直观的方式观察到。图2-4的流程图显示了S-SOFM的训练学习过程，该算法分为初始化、竞争、学习、重复迭代、得到获胜神经元等步骤。

在训练学习之前，首先需要用户设定好迭代周期T、学习率和输出节点的权重初始值等主要参数。针对输入的训练数据，设输入的数据样本的特征维度为N，共有L个训练样本，则输入样本空间X=［x₁，x₂，x₃，…，x_L］^T，x_i是样本空间中第i个输入的训练样本，i=1，2，…，L；每个训练样本都是一个N维特征向量，因此x_i=［x_i1，x_i2，x_i3，…，x_iN］^T。输出空间Y的节点数为M，则Y=［y₁，y₂，y₃，…，y_M］^T，由于每一个节点都有一个对应的权重向量，因此输出节点的权重向量矩阵为W=［w₁，w₂，w₃，…，w_M］^T，w_k表示第k个输出神经元的权重向量值。由于每个输出神经元的权重向量初始值互不相等，因此w_k的权重向量初始值是［0，1］区间内的随机值。此外，向量Φ表示每个节点被更新的频率，Φ=［φ₁，φ₂，φ₃，…，φ_M］^T，初始值为0，被用来平衡各输出节点的活跃度。η（t）是学习率参数，初值为η（0）［0＜η（0）＜1］。

在输入空间样本中随机选择一个样本x_i作为输入神经元，D_k（t）则是当前时刻输入的特征向量x_i（t）和第y_k个输出节点的权重向量之间的相似性度量差值，公式如下：

}gsr}0086-1.jpg}/gsr}

根据上面的相似性度量算法，每一个输入的x_i特征向量在输出的球体空间中都会有一个获胜神经元节点y_win，这是球体中和输入的x_i具有最大相似度（最小距离）的节点，也被称为最佳匹配单元，表示为y_win=argmin{D_k}。

学习即调整获胜神经元节点及其相邻单元节点的权重向量值，也就是说，依据下列公式对输出的获胜神经元节点在邻域h（r）内的所有神经元权重值进行修正。

}gsr}0087-1.jpg}/gsr}

}gsr}0087-2.jpg}/gsr}

}gsr}0087-3.jpg}/gsr}

在上面的公式中，h（t）表示高斯拓扑邻域函数，r是有效的邻域半径。在t时刻，d_r（y_k，y_win）表示y_k和获胜神经元节点y_win之间的距离，通常此距离越大，对权重的影响越小。η（t）是学习率参数，我们把它定义为如下形式：

}gsr}0087-4.jpg}/gsr}

T是可以迭代的最大次数，而t=1，2，…T，代表该节点当前的迭代次数，其中学习率参数的值在迭代中将不断地变小。

将下一个输入样本提供给SOFM的输入层，返回“学习”步骤，直至样本全部被提供一遍。如果学习过程满足由用户设置的“循环”参数（周期数）的停止条件，则训练过程将终止。

SOFM和S-SOFM训练学习算法的实用指南

相关推荐