多线性主成分规整在人体动作识别中的应用

2023-10-28 理论教育版权反馈

【摘要】：近年来，有的研究者引入核函数概念进行非线性映射分析，分别提出核主成分分析[121]和核判别分析[122]方法。因此，本书使用多线性主成分分析[118]算法进行特征降维。常用的一种非线性规整算法称为动态时间规整。动态时间规整算法的优点是简单，易于实现。DTW 算法就是实现参考样本和测试样本之间的非线性映射，寻找最佳的匹配路径，使累积失真最小。已知矩阵可用二阶张量表示。

上一节详细分析了基于骨架关节点运动轨迹进行动作特征表示方法，提出了张量形状描述子。骨架关节点的运动轨迹是一个高维的时间序列，具有较高的空间复杂度。因此，有必要进行特征降维，即空域压缩。人体动作识别是对多种类型的动作序列进行识别，每个序列的动作持续时间不一致，动作变化速度也不一样。因此，需要将所有的样本统一到相同的长度，即时域对齐。

（1）特征降维

研究中，常用主成分分析（Principal Component Analysis，PCA）[119]和线性判别分析（Linear Discriminant Analysis，LDA）[120]两种算法进行特征降维。该算法主要用于线性映射，对特征维度之间的非线性关联不是很理想。近年来，有的研究者引入核函数概念进行非线性映射分析，分别提出核主成分分析（Kernel Principal Component Analysis，KPCA）[121]和核判别分析（Kernel Discriminant Analysis，KDA）[122]方法。之后，又有学者在此基础上提出非参数化核判别分析（Kernel Nonparametric Discriminant Analysis，KNDA）[123]和多核判别分析（Multiple Kernel Discriminant Analysis，MKDA）[124]算法。

基于核函数进行特征降维，关键问题是选择合适的核函数及其参数，即对核函数进行优化。核函数优化常用的方法是k-折交叉验证（k-fold Cross Validation，CV）[125]，即将训练集分为k 个不相交的子集，每次从分好的样本子集中拿出一个作为测试集，其余k-1 个样本子集作为训练集，选取分类准确率最高的核参数，依次进行k 次迭代，得到最优的核参数。近几年，有的学者还提出基于Fisher 准则的核参数优化方法[126-128]。交叉验证方法不适合样本数不足的情况，运算复杂度高，而基于Fisher 准则的核参数优化方法，运算复杂度低，但无法优化降维参数。本书提出的基于骨架关节点建立的张量模型是一个线性高维数组。因此，本书使用多线性主成分分析（Multi-linear Principal Component Analysis，MPCA）[118]算法进行特征降维。

（2）时域对齐

时域对齐是指两个不同时间长度的序列进行最优匹配。常用的一种非线性规整算法称为动态时间规整（Dynamic Time Warping，DTW）。它是将时间规整和距离测度结合起来进行时间序列匹配，沿路径进行搜索，当时间序列的匹配代价函数最小时，就得到最优的匹配路径。Corradini[129]使用DTW算法，有效解决了轨迹长度不匹配时的时域对齐问题。动态时间规整算法的优点是简单，易于实现。Zhou 等[130]将正则相关分析方法与DTW 算法相结合，提出正则时间规整（Canonical Time Warping，CTW）算法，实现了对不同时间维度序列的时域对齐。本书基于张量模型进行动态时间规整，提出张量动态时间规整（Tensor Dynamic Time Warping，TDTW）算法。

给定一个参考样本X=和测试样本Y=，样本长度分别为n 和m，其中，m ＜n。DTW 算法就是实现参考样本和测试样本之间的非线性映射，寻找最佳的匹配路径，使累积失真最小。假定匹配路径W={w1，w2，…，wr…，wk}，其中，k 为路径长度，wr=（i，j）r表示匹配路径上第r匹配点是由xi和yj构成。其失真距离可表示为

为了使路径上所有匹配点的累积失真距离最小，搜索最优路径为

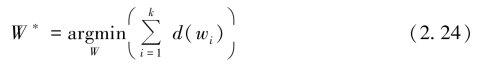
pagenumber_ebook=39,pagenumber_book=31

在搜索最优路径过程中，为了保证匹配过程的完整性和连续性，加入了边界限制条件，即匹配路径必须从第一点开始到最后一点结束，而且整个过程不允许有跳跃现象，必须随着时间单调进行且由相邻的匹配点对连接而成。因此，路径上任意匹配点wr=（i，j）和前一点进行匹配，只能从（i-1，j），（i，j-1）或者（i-1，j-1）中进行选择，累积距离的递推为

pagenumber_ebook=39,pagenumber_book=31

其中，D（1，1）=d（1，1）。

由此可知，通过DTW 算法可对时间序列进行规整，使匹配过程中的累积失真距离达到最小，从而消除序列之间的时间差异，解决时域对齐问题。

下面将使用DTW 思想分析张量空间的时域对齐问题。已知矩阵可用二阶张量表示。给定两个向量矩阵X ∈RN×n和Y ∈RN×n，用二阶张量表示为（A）ij和（B）ij，则存在关系为

其中，DTW 算法使用一个共享模式（索引i）和一个j-mode 乘积，U 和V 均为转换矩阵。

点集序列可表示为具有3 个空间轴（X，Y，时间T）的三阶张量（A）ijk∈RI×J×K，具有共同的索引（i，j，k）。因此，可使用节点共享模式来共享任意的两个空间轴（即一个平面），单独对剩下空间轴的向量进行时间规整运算。TDTW 可视为3 个不同空间轴上DTW 的集合，即矢量IJ 平面（k-mode 乘积）、矢量JK 平面（i-mode 乘积）和矢量IK 平面（j-mode 乘积）。例如，mode-j 向量是矩阵（A）j∈RJ×（IK）的列向量，那么张量A 的j-mode 乘积就可通过转换矩阵U ∈RN×J表示为

其中，j-mode 乘积和mode-j 矢量矩阵关系为

基于以上分析，假定使用的训练集包含S 个动作序列，将每个序列用张量形状描述子进行表示，得到集合。首先确定训练集中最长序列长度tL，给定张量样本A ∈Rs×λ×t和参考样本Aref∈。根据式（2.24）进行最优路径规整，其中，d（i，j）表示二阶张量Xi∈Rs×λ，Yi∈Rs×λ之间的Frobenius范数，即

(www.chuimin.cn)

D（i，j）表示到A 的第i 帧和Aref的第j 帧的总距离。定义一个扩展矩阵W ∈，将每个时间序列的长度扩展到tL。通过优化规整路径使得扩展矩阵W 每一列只包含一个元素1，其余元素全为0。例如，一个时间长度为7 的样本序列规整到长度为9 的参考序列，使用DTW 算法求得的规整路径如图2.3（a）所示。若将较短序列对齐到参考序列，则可将规整路径中每列取一个非零元素，得到扩展矩阵W，如图2.3（b）所示。遍历整个训练集，得到规整以后训练集则有

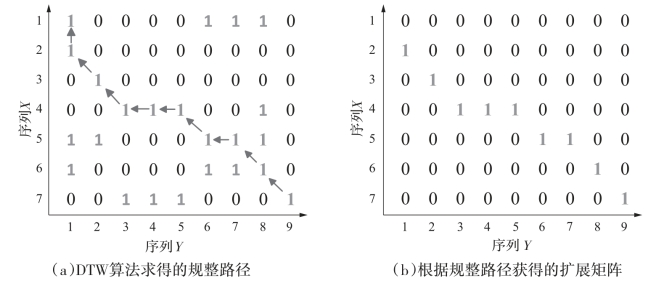
pagenumber_ebook=41,pagenumber_book=33

图2.3　序列时间对齐示意图

（3）MPCW 算法框架描述

解决时域对齐问题之后，紧接着进行空域压缩。已知张量模型是一个多维独立的高维数据，本章使用多线性主成分分析（Multi-linear Principal Component Analysis，MPCA）算法实现特征降维。该算法通过一组映射矩阵，将训练集映射到低维张量空间。例如，给定一组映射矩阵i=1，…，N}，则映射得到的低维张量空间为

其中，Pi＜Ii，i=1，2（训练集为三阶张量）。

多线性主成分规整算法框架主要分为4 个步骤，如图2.4 所示。

pagenumber_ebook=41,pagenumber_book=33

图2.4　多线性主成分规整算法框架示意图

算法步骤：

①输入张量形状描述子。由于每类动作序列长度不一致，在构造张量模型之前，先对每类动作序列进行遍历，将最长序列作为参考序列，参考序列的长度作为张量模型的一个模。因此，整个训练集可用一个四阶张量A ∈表示。其中，S 表示骨架关节点数目，λ 表示选取的上下文点数目，tL表示一类动作序列中最长序列长度值，n 表示一类动作不同受试者采集的样本数。若集合包含S 类个动作序列，该数据集就表示为

②张量动态时间规整。从集合中选择最长时间序列作为时域对齐的参考序列，使用TDTW 算法为每个张量样本计算扩展矩阵Wi∈其中，ti表示集合中第i 个动作时间序列长度，tL表示参考序列长度。遍历整个训练集，根据式（2.22）计算得到一个时间维度归一化的训练集

③多线性主成分分析。首先进行初始化，对作特征值分解。其中，表示规整后训练集A′ 的i-mode 展开，然后将降维矩阵中的U（i）设置为φ（i）最大的Pi个特征值所对应的特征向量。

下面计算U（2）和U（3），假定输出的子空间张量为B ∈，则子张量

将B′=按1-mode 展开，得到矩阵B（1），对φ（1）=作特征值分解，求得最大的P1个特征值所对应的特征向量，并更新U（1）。同样，将B′按2-mode 展开，得到矩阵B（2），对φ（2）=作特征值分解，求得最大的P2个特征值所对应的特征向量，并更新U（2），使用同样的方法更新U（3），重复迭代求解映射矩阵若干次，直到收敛，得到最终的U（1），U（2），U（3）。

④输出张量计算。经过步骤①—步骤③处理后，可计算张量子空间为

解决了时域对齐和空域压缩问题后，紧接着进行动作分类。人体动作识别研究中常用分类算法有决策树分类法[131]、神经网络[132]、最近邻分类器（k-Nearest Neighbor，KNN）[133]及支持向量机（Support Vector Machines，SVM）[134]等。决策树分类法能在较短时间内通过静态测试对模型进行评测，得到较好的结果，但易出现过度拟合问题。神经网络分类的准确度较高，但需要很长的训练时间和大量数据。KNN 算法主要依靠近邻域样本进行所属类别的确定，更适合处理类域的交叉或重叠较多的待分样本集。支持向量机的核心思想是寻找目标函数的全局最小值，而大部分分类算法都是采用贪婪学习策略进行空间搜索，一般只能获取局部最优解。

以上介绍的是一些常用的分类方法，还有其他分类算法，如遗传算法、逻辑回归和Adaboosting 方法等。本章中提出的张量模型是一个多维的线性结构，并且采用线性映射进行特征降维，故选择KNN 分类算法进行动作分类。

多线性主成分规整在人体动作识别中的应用

相关推荐