张量形状描述子在人体动作识别中的应用

2025-09-30 理论教育版权反馈

【摘要】：形状描述子三维轨迹的形状描述子是对各个离散轨迹点之间位置关系的一种表示。曲率表示运动轨迹曲线的局部形状变换，提取多尺度下曲率的过零点值，即空间极值点，将其作为形状描述子，这种方法称为曲率尺度空间。下面对3 种常用的形状特征描述子作简要介绍。该距离集合就是中心距函数形状描述子。根据上述分析，将利用欧氏距离描述运动轨迹形状的描述子，称为完整形状描述子。该完整形状描述子具有旋转、尺度和平移不变性。

通过骨骼模型描述整个人体动作主要是依靠骨架关节点在三维空间的多条运动轨迹来实现的。运动轨迹是物体在时间维度上的位置变化。对三维运动轨迹进行表示和识别的一个重要问题是如何实现运动轨迹的旋转、尺度、平移（Rotation，Scale，Translation，RST）无关性。当旋转、平移、尺度、镜像变换的影响被移除后，物体的形状特征就是所有剩余几何特性的集合[109]。

（1）形状描述子

三维轨迹的形状描述子是对各个离散轨迹点之间位置关系的一种表示。它用来描述轨迹形状特征的方法，包括小波描述子[110]、曲率[111]、混合描述子[112]、形状上下文[113]及曲率尺度空间[114]等。小波描述子是利用小波分解和重构，对每个维度的运动轨迹曲线进行小波变换，提取不同尺度的细节系数，然后进行小波重构，利用重构后的运动特征信息进行人体动作识别。曲率表示运动轨迹曲线的局部形状变换，提取多尺度下曲率的过零点值，即空间极值点，将其作为形状描述子，这种方法称为曲率尺度空间。该方法提取的特征维度较低，稳定性较好。还可通过曲线拟合的方法描述运动轨迹曲线，将轨迹表示成不同阶次的基函数组合，如B-样条曲线等。下面对3 种常用的形状特征描述子作简要介绍。

1）曲率尺度空间形状描述子

曲率尺度空间（Curvature Scale Space，CSS）形状描述子是指将图像轮廓的曲率过零点集合中的极值点和尺度信息提取出来，作为形状描述子。假设曲线的方程为L（s）= {x（s），y（s）}，其中，s 为弧长。可计算各点的曲率为

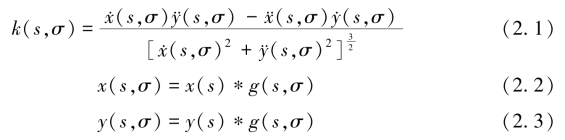
pagenumber_ebook=31,pagenumber_book=23

其中，g（s，σ）为高斯函数；分别表示x（s，σ）的一阶和二阶导数；分别表示y（s，σ）的一阶和二阶导数。通过式（2.4）绘制曲率k（s，σ）曲线，其中，横坐标表示弧长的值，纵坐标表示尺度值。在弧长一定的条件下，求取局部极值点，从而构建曲率尺度空间形状描述子

pagenumber_ebook=31,pagenumber_book=23

2）中心距函数形状描述子

中心距函数（Centroid Distance Function，CDF）是一种利用几何特征进行形状描述的表示形式。对空间的曲线求取几何中心，即

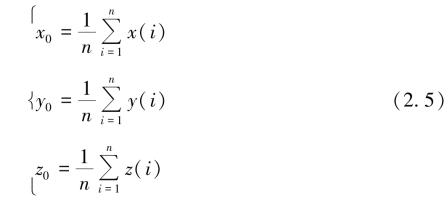
pagenumber_ebook=32,pagenumber_book=24

计算曲线上各点到几何中心的欧氏距离。该距离集合就是中心距函数形状描述子。该描述子可大致反映曲线的形状信息，但不能描述局部细节，是一种全局形状描述子。

3）傅里叶描述子

傅里叶描述子（Fourier Descriptor，FD）是一种利用频域特征表示形状的描述子。它通过对目标边界曲线进行傅里叶变换。边界曲线上点的复数形式为

进行傅里叶变换

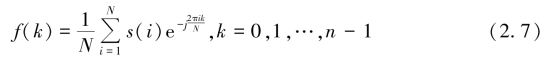
pagenumber_ebook=32,pagenumber_book=24

依次对边界曲线上采样点的傅里叶变换系数取模，并进行归一化处理，得到的集合就是傅里叶形状描述子。

使用轨迹形状进行图像轮廓特征描述，最具有代表性的一种描述方式就是形状上下文[113]。形状上下文主要是完成目标轮廓的物体匹配，它对目标轮廓进行点采样，假设一共采样N 个点，那么在轮廓空间位置中的任意一点就可由其他N-1 个采样点来唯一确定。目标轮廓的采样点越多，就会有更多点产生上下文关系，对目标轮廓的描述也就越精确。随后按照角度和距离进行区域划分，统计区域内的点，作为形状特征和目标轮廓进行匹配。虽然使用形状上下文描述子可得到较好的效果，但其包含大量的冗余信息，不具有紧凑结构，不能作为一种完整形状描述子。

总而言之，上述方法虽然能取得较好的识别效果，但这些描述子都不能完整地提取形状信息，在理论和实际应用中尚有较多问题亟待解决。

本节通过运动轨迹点之间的欧氏距离集对运动轨迹进行描述。假定一条运动轨迹存在n 个点，djk表示点集中第j 点到第k 点之间的欧氏距离，则轨迹的形状就可表示为{djk}j=1，…，n-1，k=j+1，…，n，基于欧氏距离集对运动轨迹进行描述的具体理论证明可详见参考文献[115]。下面对该形状描述子是否能完整描述轨迹形状进行分析。

假定在空间三维坐标系中由N 个不同点组成的运动轨迹为，其N 个点之间的欧氏距离集合可表示为

如果D（N）经过等距映射后不改变轨迹形状，那么D（N）就可作为完整形状描述子对运动轨迹进行描述。等距映射可分解为旋转、平移和镜像变换的组合[116]。前文提到，形状定义为移除旋转、平移、尺度及镜像变换后物体所剩余的几何特性，即形状与旋转、平移、尺度及镜像变换无关，故

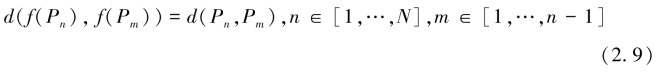
pagenumber_ebook=33,pagenumber_book=25

其中，f（·）为坐标系的等距映射，即等距映射不会改变运动轨迹形状。定义N 个不同轨迹点相互之间欧氏距离的点距集合为C（N），即

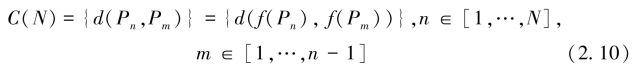
pagenumber_ebook=33,pagenumber_book=25

则C（N）包含运动轨迹TN=全部的形状信息。

下面证明运动轨迹形状由C（N）唯一决定。

假设存在另一条运动轨迹T′N= ，该轨迹的点距集合C′（N）与C（N）相同，由于 T′N和 TN都属于三维欧氏空间，定义映射g：，则存在关系为

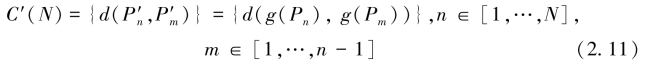
pagenumber_ebook=34,pagenumber_book=26

因此，映射为等距映射。由于等距映射不会改变运动轨迹形状，因此轨迹与TN的形状相同，即C（N）具有唯一性。

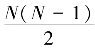根据上述分析，将利用欧氏距离描述运动轨迹形状的描述子，称为完整形状描述子。该完整形状描述子具有旋转、尺度和平移不变性。虽然完整形状描述子可保存运动轨迹全部的几何特性，但存在一个问题，对一个由N 个不同点组成的运动轨迹，特征维度为3 N，计算欧氏距离后，点距集合C（N）的特征维度为 pagenumber_ebook=34,pagenumber_book=26 ，数据的空间复杂度由O（N）增加到O（N2），空间复杂度的增加会降低动作行为识别效率，影响动作识别率。(https://www.chuimin.cn)

点距集合C（N）表示的是N 个轨迹点相互之间的欧氏距离集合，是否可选取λ 个关键轨迹点，用N 个点到这λ 个关键点的欧氏距离集合C（N，λ）来代替整个点距C（N）。

本节提出的完整形状描述子就可很好地结合上下文关系，得到一个紧凑结构。Wu 等[117]提出“点上下文”概念就是基于这种思想。

对三维运动轨迹TN=上的任意轨迹点Pm（m ∈[2，…，N]），从Pm之前（或之后）的轨迹段Tm-1（Tm+1）中选取λ 个点，构成一个新的点距集合，选取的点称为点Pm的上下文点，λ 是决定选取点的个数，称为上下文数。在选择上下文点时，需要满足以下约束条件：与Tm-1（Tm+1）的空间关系相同。定义cm为轨迹点Pm到点集的欧氏距离，即

定义C（N，λ）为轨迹点Pm（m ∈[2，…，N]）到其各自上下文点的欧氏距离，即

当λ ≥4 时，C（N，λ）是TN的完整形状描述子，具体证明详见参考文献[117]。

根据上述分析，每一个轨迹点都可由λ 个上下文点表示。因此，将C（N，λ）称为“点上下文”形状描述子，如图2.2 所示。

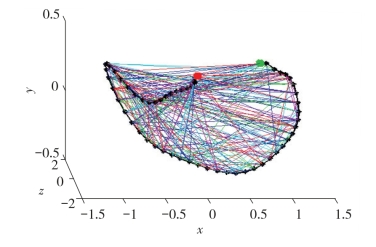
pagenumber_ebook=35,pagenumber_book=27

图2.2　“点上下文”形状描述子示意图

由于使用轨迹点之间的欧氏距离表示形状描述子，因此，该形状描述子具有尺度、旋转和平移不变性。点距集合C（N，λ）的最小维度为4 N，即对一条包含N 个点的轨迹TN的 pagenumber_ebook=35,pagenumber_book=27 个点距集合中，从中选取大约4N 个距离特征就可构成完整形状描述子。因此，点上下文形状描述子压缩了完整形状描述子的特征维度，具有更低的冗余度。但当λ 较小时，会牺牲掉一部分形状的完整性，影响动作识别率；当λ 较大时，会增加空间复杂度，降低运算速度。因此，在实际动作识别过程中，要平衡动作识别率和运算速度之间的关系，从而科学、合理地确定点上下文数λ。

综上所述，基于骨骼模型进行人体动作识别研究，可通过点上下文形状描述子进行特征表示。该形状描述子是一个含有多个维度独立的高维数组，为了解决向量输入模型引起的“维度灾难”问题，可通过建立张量模型进行人体动作识别研究。

（2）张量代数基础

张量可看成一维向量和二维矩阵的扩展，是具有多个维度的数组。张量空间是由若干个向量空间中基底的外积张成的空间，张量空间中向量空间的个数称为阶数。向量X={xi} 可称为一阶张量，矩阵X={xij} 可称为二阶张量，三阶或更高阶张量表示为X={xij…k}。本书使用粗体小写字母表示向量形式，使用粗体大写字母表示矩阵形式，使用粗体大写字母表示张量形式。一个N 阶张量可表示为。

张量是一个多重线性映射。定义一个映射：T ∶V →W。所谓的线性，是指式（2.14）和式（2.15）对任意向量x，y ∈V 和标量α 都成立，即

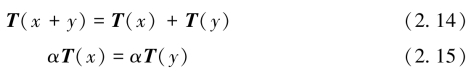
pagenumber_ebook=36,pagenumber_book=28

张量是多个向量到标量的多重线性映射，有别于一般的线性映射。假定在实数域，则有T ∶V1×V2×…×VP→R，那么P 就是张量的阶数。张量可表示成一个多维数组，因此，张量可构成一个向量空间，其维度为

假设N 阶张量X，Y ∈，则张量的内积可表示为

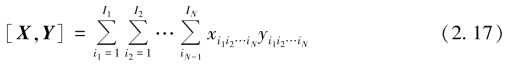
pagenumber_ebook=36,pagenumber_book=28

一个N 阶张量X ∈和一个矩阵U ∈的n-mode（矩阵）乘积表示为（X ×nU） ∈。其定义为

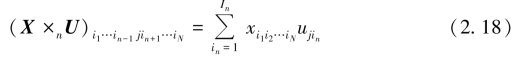
pagenumber_ebook=36,pagenumber_book=28

式（2.18）可写成沿mode-n 展开的形式，即

n-mode（矩阵）乘积具有性质

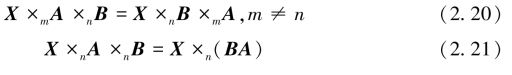
pagenumber_ebook=36,pagenumber_book=28

一个N 阶张量X ∈和一个向量V ∈的n-mode（向量）乘积表示为∈。其元素定义为

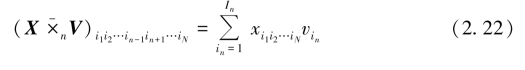
pagenumber_ebook=37,pagenumber_book=29

（3）张量模型

根据上述分析，可通过点上下文形状描述子进行特征描述，即对每个轨迹点选取满足约束条件的λ 个上下文点，求取轨迹点到上下文点之间的距离，使用距离矩阵作为描述轨迹形状的特征向量。假设本书研究的骨骼模型，每帧骨架包含K 个三维点，若提取λ 个上下文点来表示每帧的空域信息，需要Kλ 个特征向量，对一个长度为T 帧的动作序列，需要KλT 个特征向量描述全部帧信息。该特征向量进行特征值分解时，时间复杂度达到O（n3），导致较为严重的“维度灾难”现象。因此，需要一种更有效、合理的特征表示方法。

在基于张量处理高维数据的应用研究中[118]，本章引入张量运算，将一类动作序列的骨骼点序号、点上下文序号、帧数作为张量的3 个模，该类动作序列就可用一个三阶张量A ∈RKλT表示，称为张量形状描述子。在进行特征值分解时，张量按照模的展开进行迭代求解，三阶张量可按照1-mode 展开、2-mode 展开、3-mode 展开作为输入量，则运算复杂度相当于O（K3） + O（λ3） +O（T3），远低于作为向量输入的运算复杂度O（K3λ3T3）。又因张量可对多个维度的数据进行独立运算，不会破坏另一个维度之间的相关性，能更好地保留数据结构信息，非常适合处理像骨骼模型这种具有多个维度独立的高维数据。因此，本章引入张量形状描述子表示动作序列。

张量形状描述子在人体动作识别中的应用

相关推荐