从数据库里检索数据所涉及的活动称为查询处理。对于一个高级查询，DBMS可以使用不同的技术处理、优化和执行。在高级查询语言里，任何一个给定的查询可以有不同的处理方式，每个查询需要的资源也是不同的。图6.1SQL查询命令的执行步骤......
2023-10-28
分布式数据库技术：查询并行化
【摘要】：尽量要求事务执行能够并行化。图14.16Teradata DBC的事务处理是并行的图14.16中，每个竖放的矩形表示处理器，分别记为AMP1、AMP2、AMP3和AMP4，横放的矩形表示事务。图14.18算符内并行注：为算符，为算符实例i，n=并行度2.算符间并行算符间并行指的是不同的算符并行计算。图14.19中的两个选择算符是独立并行的。算法14.2是并行关联连接算法。
尽量要求事务执行能够并行化。例如，Teradata DBC中的事务处理是并行的，如图14.16所示。
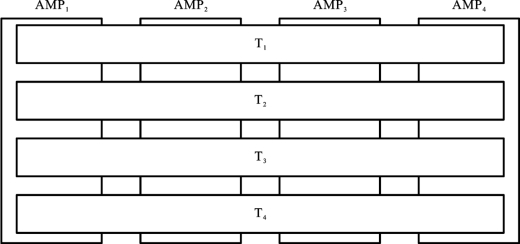
图14.16 Teradata DBC的事务处理是并行的
图14.16中，每个竖放的矩形表示处理器（AMP），分别记为AMP1、AMP2、AMP3和AMP4，横放的矩形表示事务。由图可见，在Teradata DBC中，假如有四个事务T 1、T 2、T 3和T4，每个事务的运行都由处理器（这里是AMP）承担了。由此可以看出，AMP均衡地承担事务处理功能。
在Teradata DBC中，事务运行是一回事，数据存取又是一回事，数据存取是按照数据如何存放来实施的，如图14.17所示。
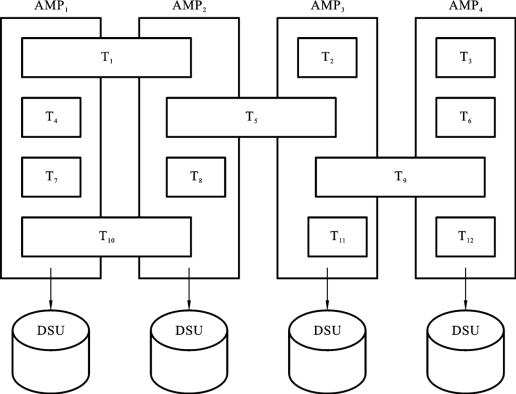
图14.17 Teradata DBC中的数据存取
由图14.17可知，数据存取时，并不是所有的AMP都均衡参与，而是只与存放相关数据的AMP有关。例如，由于事务T 1涉及的数据由AMP1和AMP2管理，所以其执行只涉及AMP1和AMP2。
事务的并行包括查询处理并行，我们在这里讨论查询处理并行问题，讨论算符内并行和算符间并行两种情况。
查询处理并行可以并行执行并发事务生成的多个查询，以增加吞吐量。算符间并行和算符内并行用于节省响应时间。算符间并行是通过在几个处理器上并行执行查询树的几个算符获得。而算符内并行指的是几个处理器为一个算符服务。
1.算符内并行
算符内并行指的是把一个算符分解成若干个子算符（称为算符实例），然后分别实现（见图14.18）。这种分解是通过将关系静态或动态分割来实现的。这样，每个算符实例处理一个关系分割（也称吊桶）。算符分解常常获益于数据的初始分割（如数据按连接属性分割）。为了说明问题，我们来看一个简单的“选择-连接”查询。选择算符（σ）均可直接分解成几个选择算符，每个算符操作在不同的分割上。如果关系是按照选择属性分割的，分割性质可以用来消除某些选择实例。例如，在一个精确匹配的选择里，只需有一个选择实例被执行（如关系是按照选择属性、采用哈希（或分类）方法来分割的）。对于连接算符（∞）来说，分解过程要复杂些。很可能关系R的每一个分割Ri必须和整个S关系作连接，这种连接效率很低（除非S很小）。原因是要将S广播到分割所在的所有处理器。好点的解决方法是将S按连接属性分割，使得连接与两个关系的分割一一对应，形成简单连接图。但是这种方法比较难实现，因为这两个关系的原始分割依据可能是不一致的。
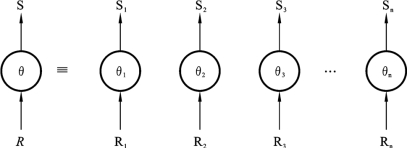
图14.18 算符内并行
注：
为算符，
为算符实例i，n=并行度
2.算符间并行
算符间并行指的是不同的算符并行计算。其实，还有两种算符间并行模式：流水线并行和按生产者-消费者（producer-consumer）连接方式并行执行。例如，图14.19所示的选择算符（σ）独立并行执行，接着是连接算符（∞）。这种执行方式的好处是，中间结果无需再实体化（materialized），从而节省了内存和磁盘存取空间。图14.18里，只有S放在内存里。注意，这里的独立并行（independent parallelism）指的是并行执行的算符之间没有依赖性。图14.19中的两个选择算符是独立并行的。
3.并行数据处理
分割后数据的定位是数据库查询并行执行的基础。如果要指定分割后数据的定位，主要是设计有效的数据库算符（如关系代数算符）和由多个算符组合的数据库查询的并行算法。这个问题实现起来不容易，因为需要在并行度和通信开销之间达到一个合理的折中。关系代数算符的并行算法是并行查询处理必需的构成模块。我们再用图14.19来说明。
如图14.19所示，假设有三个算符：两个选择算符和一个连接算符。可以先实施选择算符，然后将两个选择算符（σ）的结果再进行连接算符（∞）算符，这两个选择算符可以并行处理，它们完成后就可以实施连接算符。
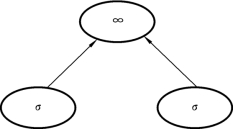
图14.19 算符间并行
并行数据处理还应当考虑算符内并行。定位分割数据时选择算符的处理方式和前面讲的分布式数据库系统总分片数据库时的情况相同。按照选择谓词，一个算符可以在一个节点执行（准确匹配谓词时），也可以在面临任意复杂谓词时涉及与分割关系相关的全部节点。
连接算符的并行处理要复杂得多。为高速网络设计的分布连接算法可以成功地应用到并行数据库的分割数据环境。下面我们讨论分割数据库的三个基本并行算法：并行嵌套循环（parallel nested loop，PNL）算法、并行关联连接（parallel associative join，PAJ）算法和并行哈希连接（parallel hash join，PHJ）算法。为了说明问题，我们在下面的伪程序中使用了do in parallel结构。
do in parallel可以说明下面的程序块是并行执行的。
for i f rom 1 to n do in paral lel ac t ion A
/＊说明：ac t ion A由n个节点并行执行＊/
我们把R或S的一个数据片驻留的节点，称为R-node（或S-node）。
并行嵌套循环算法是最简单也是最常用的算法。本质上，它是并行运行R和S的笛卡儿积。因此可以支持任意复杂的连接谓词。下面描述这个算法，令连接结果生成在S节点。算法分为两个阶段。
算法14.1
现在分析这个算法。在这个算法的第一阶段，将R的每个数据片发送和复制到放有Sn数据片的每个节点（假设有n个节点）中。这一阶段可以在m个节点（若R有m个数据片）并行操作，如果通信网络有广播功能，则会非常有效。此时一次广播就能将数据传输到n个节点。总的发送消息数为m。否则需要发送消息数为（m*n）。
在第二阶段，每个存放S数据片的节点j接受整个R关系，执行R和数据片Sj的本地连接。这个阶段可以由n个节点并行操作。本地连接的实施和集中式DBMS的相同。连接处理不一定是一接到发送来的数据就启动，如嵌套循环这种连接算法可以在一接到发送来的数据就执行连接，而排序归并算法则必须等所有数据都收到后再执行连接。
总之，并行嵌套循环算法是将R∞S替换为：
【例14.1】 图14.20是关于并行嵌套循环算法应用的例子，这里m=n=2。(www.chuimin.cn)
算法14.2是并行关联连接算法。现在来考虑等连接（equijoin）[9]，令操作数关系是按连接属性分割的。为了简化算法描述，假设等连接谓词涉及的是R的A属性，S的B属性。更进一步，关系S是对连接属性B按哈希函数h分割的，意味着将满足h（B）的元组放在同一个节点。目前R究竟如何分割尚无确切定论。我们令并行关联连接算法产生的结果放在Si所在的节点上。
算法14.2
图14.20 并行嵌套循环算法应用的例子
算法14.2里，第一阶段，将关系R发送到相关的存放S关系数据片的节点（简称S节点），它是对属性A采用哈希函数h运算而使两者相关的。这保证了R的哈希值为x的元组能发送到含有哈希值也为x的元组的S节点。第一阶段由Ri驻留的m的节点并行执行。与并行嵌套循环算法不同的是，R的元组是分布到而不是复制到S节点。在第二阶段，每个S节点j并行接受R的子集（如Rj），在本地与S的分片实施连接。本地连接处理可以使用并行嵌套循环连接算法。
总之，并行相关连接算法是将算符R∞S替换为：
【例14.2】 图14.21是一个并行相关连接算法的应用样例，其中m=n=2。矩形形态的相仿与否表示连接双方的关联性。
并行哈希连接如算法14.3所示。这可以看成是并行关联连接算法的泛化。基本思路是将关系R和S分割成相同个数p的互斥集合（数据片）R1，R2，…，Rp和S1，S2，…，Sp，从而
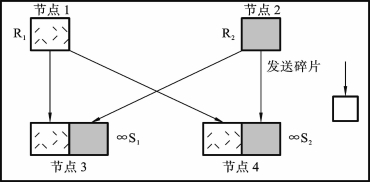
图14.21 并行相关连接
算法14.3
就像并行相关连接算法一样，R和S的分割可以通过在连接属性上按相同哈希函数映射来实施。每个单独的连接（Ri∞Si）是并行执行的，连接结果则在p节点产生。这些p节点的选择可在运行时根据系统负载来决定。和并行相关连接算法的差别是，这里必须分割Sn（n=1，2，…，n），结果生成为p个（对应p个节点）而非n个（对应S节点数n）分割。
图14.22是并行哈希连接算法的应用例子，其中m=n=2。我们假设结果产生在节点1和节点2。因此，从节点1到节点1、从节点2到节点2有优先箭头表示本地（本节点）传输。
这些并行连接算法的应用和控制与不同的条件有关。连接处理的并行度可以是n或p（哈希吊桶数）。每个算法都要求至少移动一个操作数关系。为了比较这些算法，将总开销分为总通信开销（记为CTR）和处理器开销（记作CCPU）。因此总开销为：
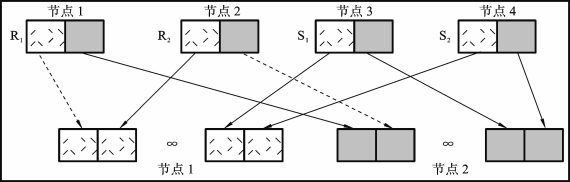
图14.22 并行哈希连接
Cost（Alg.）=CTR（Alg.）+CCPU（Alg.）
为了简化，CTR不包括控制消息。这里，用msg（＃tup）表示从一个节点传输一个消息到另一个节点的开销。处理器开销（总的I/O开销和CPU开销）可以用一个函数CLOC（m，n）来表示，它表示的是分别为m和n的两个关系连接时的本地计算开销。我们假设在这三个并行连接算法里，本地连接算法是相同的。最后我们假设并行完成的工作是均匀分布在算符的所有节点上的。
4.并行嵌套循环算法
若没有广播功能，那么使用并行嵌套循环算法需要发送m*n个消息的开销，每个消息包含的R关系数据片的大小为card（R）/m。从而，CTR（PNL）=m*n*msg（card（R）/m）。
每个S节点必须和全部R与其对应的S数据片连接。这样，得到CCPU（PNL）=n*CLOC（card（R），card（S）/n）。
5.并行关联连接算法
并行关联连接算法要求每个R节点将R的数据片分成n个子集，大小为card（R）/（m*n）并将之发送到n个S节点。这样得到CTR（PAJ）=m*n*msg（card（R）/（m*n））和CCPU（PAJ）=n*CLOC（card（R）/n，card（S）/n）。
6.并行哈希连接算法
并行哈希连接算法要求关系R和S都按p个节点分割，类似于并行关联连接算法。这样我们得到CTR（PHJ）=m*n*msg（card（R）/（m*p））+n*p*（card（R）/（m*p））和CCPU（PHJ）=n*CLOC（card（R）/n，card（S）/n）。
我们假设p=n，此时PAJ和PHJ算法的连接处理成本相同。但是，PNL算法的成本要高些，原因是每个S节点必须实施与整个R的连接。从上面等式看，PAJ算法发生的通信开销最少。然而，PNL和PHJ算法间通信开销取决于关系基的值和分割的度。如果选择恰当，使p小于n，则PHJ算法可以产生最少的通信开销，但增加了连接处理开销。例如，如果p=1，则连接按纯集中方式处理。
总之，PAJ算法最受欢迎。相反，在PNL和PHJ算法间做选择，需要估算开销。但实施时，可以酌情选择合适的算法，算法14.4是一个选择算法。
算法14.4
有关分布式数据库技术的文章
- 详细阅读
-
优化分布查询算法-分布式数据库技术详细阅读
表7.8分布查询优化算法比较①统计内容分别为：1=关系的基，2=每个属性的不同值个数，3=连接选择系数，4=每个连接属性上投影的大小，5=属性大小和元组大小。......
2023-10-28
-
分布式数据库技术：涉网查询优化概述详细阅读
涉网查询优化的问题主要包括三部分，其过程简述如下。查询优化器可以由三个成分构成：搜索空间、成本模型和搜索策略。图7.17查询优化过程1.搜索空间查询执行计划是算符树的一种表现形式，对执行序有更明确的表示，有丰富的附加信息，如为每个操作选择最佳实施方法。图7.19连接树的两种主要形态2.搜索策略查询优化器最常用的搜索策略是动态规划，称为确定策略。......
2023-10-28
-
分布式数据库技术：查询分解和重写的案例详细阅读
查询分解的最后一步是将查询重新写成关系代数的形式。重构关系代数查询以改进性能。树根则代表查询结果。其次，根节点是关于结果属性的投影操作，显示在Select子句中。 查询“那些在CAD/CAM项目中工作了1年或2年的名字不叫李林的雇员”，其SQL语句如下：Select enamef rom PROJ，EMP_PROJ，EMPwhere EMP_PROJ.eno=EMP.enoAND EMP_PROJ.pno=PROJ.pnoAND ename≠"李林"AND PROJ.pname="CAD/CAM"AND这可以映射成图7.2所示的算符树。应用变换规则，从这棵算符树可以派生出许多不同的树。如何重写，请看下面即将介绍的等价变换。图7.2算符树的例子......
2023-10-28
-
分布式数据库技术：对象查询处理器详细阅读
几乎所有的对象查询处理器都使用关系型系统定制开发的优化技术。通过继承层次存取对象的优化也是面向对象和关系查询处理相区别的问题。图15.8对象查询处理方法对象的复杂结构及其上面提及的那些与关系查询的四点主要差异导致对象查询的优化和关系查询比较有很大不同。查询优化器可以计算整棵处理树的成本。......
2023-10-28
-
分布式数据库技术中的本地化查询详细阅读
查询分解是把分布演算查询映射到一个全局关系的代数查询上。从代数优化看，使用直接分步骤的算法可以获得一个“好的”结果，但是，进一步看未必是最佳的。换句话说，每次选最好的，不见得最终结果是最佳的。就像有一筐苹果，每天选一个质量最好的苹果吃，不见得是最好的吃法。数据定位决定查询涉及哪些数据片，并将分布查询转化成分片查询。......
2023-10-28
-
查询处理：实现目标分布式数据库技术详细阅读
查询处理的目标是按照分布式上下文将基于分布式数据库的高级查询转换成采用低级语言表达的、更有效的、基于局部数据库的执行策略。响应时间是执行查询获得响应所经历的时间。集中式数据库系统中，总开销主要由CPU开销和I/O开销构成。CPU开销是指数据在内存时发生的计算开销。通信开销则是参与执行查询的节点间交换数据所需的开销。大部分早期的分布式查询处理的建议方案都强调通信开销远大于本地开销，因此可以忽略本地开销。......
2023-10-28
-
查询优化器体系结构：分布式数据库技术解析详细阅读
查询优化器体系结构如图6.2所示。图6.2查询优化器体系结构查询优化器的工作过程一般分为两个阶段：重写阶段和规划阶段。在集中式系统中，查询执行策略可以很好地使用扩展关系代数来表示。集中式查询处理器的主要角色是为给定查询根据等价原理选择最好的关系代数查询表达形式。同时，除了要选出关系代数运算的顺序外，分布查询处理器还需确定最佳的运算执行节点。......
2023-10-28
相关推荐