分布式数据库技术：事务与事务管理

2023-10-28 理论教育版权反馈

【摘要】：事务和事务管理是数据库系统中的两个重要概念。图8.1事务模型图8.1中，事务T将数据库从一致状态转换成另一个一致状态，事务执行期间，数据库可能临时处于不一致状态。事务管理就是这样一种机制，它负责让数据库始终保持一个一致状态，即便是并发存取或发生故障。例8.1中有一个假设，即事务总是会按目的终止。如果事务成功完成，我们称为事务提交。事务夭折的原因多种多样。

事务和事务管理是数据库系统中的两个重要概念。

为了有效地管理数据，DBMS需要提供一个良好的环境来存放和检索数据，使之更经济和有效。用户可以发布指令（一般称为查询）存放和检索数据。这个过程在DBMS里用一个专用词汇“事务”来表示。

可能会有当两个查询同时读取一个相同数据项时的情况出现。如果出现故障，那么只读（read-only）查询就可以简单地重新启动，但是修改操作不能简单地重新启动。原因是有些数据很可能在故障发生前已经被写进了数据库。重新启动后，如果重复已经写过的数据，那么会出现不正确的数据。

这里产生的基本问题是，查询的一致计算问题和可靠计算问题。数据库系统中广泛使用事务的概念，作为一致计算与可靠计算的单位。下面介绍数据库一致性与事务一致性的区别。

数据库如果服从给它定义的所有一致（完整）性限制，则认为处于一致状态。当实施修改、插入和删除（统称为更新）操作时，数据库状态会发生变化。当然，我们希望数据库不要进入不一致状态。但是，在事务执行期间，数据库总会进入暂时的不一致状态。因此，重要的是，在事务结束的时候数据库必须进入一致状态。图8.1给出的是一个事务模型的描述。

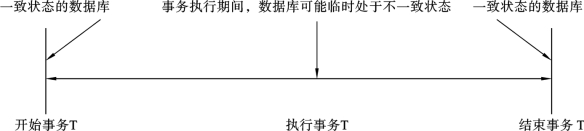
pagenumber_ebook=167,pagenumber_book=152

图8.1　事务模型

图8.1中，事务T将数据库从一致状态转换成另一个一致状态，事务执行期间，数据库可能临时处于不一致状态。

事务的一致性是指尽管事务并发操作，我们仍希望数据库保持一致状态，即使同时有许多用户请求存取（读/更新）数据库。值得注意的是，当有副本数据库存在时，这个问题会变得更复杂。副本数据库需要满足相互一致状态（mutually consistent state），即每个数据项的副本都有相同的值。假设在事务执行终结时强制所有副本满足这个条件，我们称之为单副本一致性（one-copy equivalence）。

事务的可靠性是指系统在各种故障时能自愈，有能力从故障状态恢复。一个能自愈的系统是能够容忍系统出现故障并在出现故障时仍能连续提供服务。一个可恢复的DBMS在出现各种故障后仍能达到一个一致状态（回到原来的一致状态或进入一个新的一致状态）。

事务是DBMS中用户执行的程序。与数据库系统外的程序不同，这里的程序操作主要就是数据的读操作和写操作。事务在DBMS中扮演着重要角色。不完整的事务（incomplete transaction）会导致数据库不一致，因此应当避免。

数据库的一个重要特征是共享，多个用户同时存取同一个数据是常有的事。要维护数据库的正确性和一致性，需要使用合适的调度算法。

事务管理就是这样一种机制，它负责让数据库始终保持一个一致状态，即便是并发存取或发生故障。

事务的概念源自6000年前，苏美尔人（古代幼发拉底河下游地区的居民）在黏土板上记下一些符号，以保留交易变化的信息。

事务可以说是从一个状态到另一个状态的转换。

Gray^[1]于1981年提出，事务概念在契约法中有其来源。他指出，在签订合同时，签约双方或多方协商一会儿，然后完成交易。这种交易形式是大家在文件上签字，或使用另外一个动作（如握手、点头等）来确认。如果交易方中有人对对方不放心，就会请第三方（通常称公证员）来协调事务的提交。这个概念现在被用在数据库系统中。

事务是一个一致计算与可靠计算的单位。可以说，事务将数据库从一个一致状态转换成另一个一致状态。事务可以并发执行，在其执行期间可能发生故障，但是在执行结束时数据库应当进入一个一致状态。

事务可以看成是由对数据库的读操作、写操作，加上计算操作的步骤序列构成的。

【例8.1】假设有一个SQL查询，新年以后为每个学生的年龄加一岁：

pagenumber_ebook=168,pagenumber_book=153

这里使用Begin_of_Transaction和End_of_Transaction（简称EOT）语句把一个事务范围勾勒出来。

例8.1中有一个假设，即事务总是会按目的终止。显然，这是不现实的。

事务总会终止，既可能是按目的正常终止，也可能是异常终止。

如果事务成功完成，我们称为事务提交（commit）。相反，如果事务没有完成其任务就结束，我们称为夭折（abort）。事务夭折的原因多种多样。一旦事务夭折，如由于死锁（dead lock）或其他不利条件发生，事务的执行就停止，所有已做的工作需抹去（undone，简称undo），我们也称回退（roll back）。

提交的重要性有两层意思：一层是提交的命令信号发送给DBMS，将该事务产生的效果反映到数据库里，其他想存取该数据的事务可以见到其效果。另一层是此时事务提交的节点就成为“非返回点”（point of no return）。提交事务的结果从此永久保存在数据库中，不能再抹去。

【例8.2】我们来看一个航空订票系统的例子。令Fight和FC为两个关系，分别表示航班信息和客户订票信息。这里，属性Fight.fno表示航班号、Fight.date表示起飞日期，Fight.stsold表示已售出座位、Fight.cap表示飞机容量（总共有多少个座位）。这个事务可以表示如下：

pagenumber_ebook=169,pagenumber_book=154

例8.2中的第一条SQL语句用于获得stsold（已售座位）和cap（剩余座位）数据，再把它们放到两个变量temp1和temp2里。比较这两个值，判定是否还有空座位。如果没有座位了，事务就夭折，否则就修改stsold值，在FC关系中插入一个元组，表示该座位已售出。

从前面的例子可见，事务对某些数据进行读或写，这可以看成是事务的基本特征。

事务读的数据项可以用一个数据集合来表示：R（read set）。类似地，写集合记作W（write set）。这两个集合一般不是互斥的。它们的并集记作基集（base set，B），即B=R∪W。

【例8.3】考虑例8.2的一个订票事务，其插入操作可分为若干写操作。为了方便，将关系Fight简记为F，相应的读、写和基集分别如下。

R［航班订票］={F.s t so l d，F.cap}

W［航班订票］={F.s t so l d，FC.f no，FC.date，FC.cname，FC.spec ia l}

B［航班订票］={F.st so l d，F.cap，FC.f no，FC.date，FC.cname，FC.specia l}

这里，我们将事务按“读”和“写”操作来区分，而不管“写”操作是插入、更新还是删除。同时把问题限制在一个静态数据库的事务管理概念上，即假设数据库不扩大也不缩小，这样可以简化问题。如果考虑动态数据库，还必须处理幻象（phantom）问题。幻象指的是，假如有一个事务T 1，执行期间，搜索FC表，查找有一个要求（如适合坐轮椅进出）的旅客。在事务T 1执行期间，事务T 2在FC中插入了一条符合该特殊需求的新记录。如果在执行前后T 1两次发出相同的查询请求，得到的cname集合就不相同。这样，幻象元组出现在数据库中。

需要指出的是，这里讲到的读、写操作和物理I/O操作不是一一对应的。一个读操作可以映射成几个物理读原语：存取索引结构、存取物理页面等。换言之，这种读可以看成是语言级的读和写，而不是操作系统级的原语。

这里我们希望比较形式化地对事务作一描述。为保证事务及管理算法的正确性，下面给出一个事务的形式定义。

令aij（x）记为属于事务Ti的对数据库中数据项x上实施的一个操作，aij∈｛read，write｝。假设这些操作都是原子性的。(www.chuimin.cn)

令Ai为事务Ti的操作集（即Ai=∪j aij）。我们用Ni表示事务Ti的终止条件，Ni∈｛abort，commit｝。

采用这种术语，可以定义一个事务T为其操作和终止条件上的一个偏序。

一个偏序P=｛Σ，≯｝定义了Σ（称为域，domain）中元素的一个非自反、传递的二元关系≯。Σ包含事务的操作和终止条件。

定义8.1 一个事务Ti是一个偏序，记作Ti=｛Σi，≯i｝，其中：

（1）Σi=Ai∪｛Ni｝。

（2）对任意两个操作aij，aik∈Ai，若aij=r（x），r（x）∈R或aij=w（x），w（x）∈W且aik=w（x），w（x）∈W，x为任意数据项，则aij≯iaik或aik≯iaij。