优化分布查询算法-分布式数据库技术

本节主要讨论分布INGRES算法、System R*算法和SDD-1算法，它们之间的区别如下。

●分布INGRES算法采用动态优化时间方式，其他算法则采用静态优化时间方式。

●分布SDD-1算法和System R*算法的目标函数只考虑总开销最小，而分布INGRES算法则考虑响应时间和通信时间的组合最小。

●分布SDD-1算法的优化因子只考虑消息量大小，分布System R*算法考虑的是本地处理时间、消息量大小、I/O和CPU开销。分布INGRES算法则考虑消息量大小和本地处理时间（I/O+CPU time）。

●分布SDD-1算法假设的网络拓扑是广域网点对点网。分布INGRES算法和System R*算法则适合在通用网或广播网环境工作。

●分布SDD-1算法使用半连接优化技术，分布式INGRES算法和System R*算法则采用类似集中式版本的技术。

●分布INGRES算法可以处理数据分片。

分布INGRES算法、SDD-1算法和System R*算法的比较如表7.8所示。

表7.8　分布查询优化算法比较

①统计内容分别为：1=关系的基，2=每个属性的不同值个数，3=连接选择系数，4=每个连接属性上投影的大小，5=属性大小和元组大小。

1.分布INGRES算法

分布INGRES查询优化算法源自集中式INGRES。算法的目标函数是将通信时间和响应时间组合最小化。不过，这两个目标可能是矛盾的。例如增加通信时间（并行处理）能减小响应时间。这样可以让一个的权重高一些。要注意的是，这个算法忽略了将数据传输到结果节点的开销。而且这个算法采用了数据分片技术，但只支持水平分片。

该算法也考虑网络拓扑结构，包括广播网。使用广播网可以广泛复制数据片，增加并行度。

该算法的输入是元组关系演算标识的查询（合取范式）和模式信息（网络类型中每个数据片的大小和存储地点）。算法执行的节点称为主节点（master site），是查询启动的节点。详述如下。

算法7.3 QP_D-INGRES

这个算法的基本过程简述如下。

首先，本地处理所有分离的单关系查询（如选择和投影），即ORQi。然后在原始查询上使用约简算法［Step 2］。这样，约简程序（REDUCE（））产生一个不可约简子查询序列q1→q2→→qn，其中，两个顺序相继的子查询里最多只有一个公共关系。

在Step 2分离出来的不可约简查询和每个数据片大小的基础上，找出下一个处理的子查询MVQ，并在（3.1）和（3.2）里选出两个变量（要传输的数据片和处理地点），然后应用（3.3）和（3.4）。（3.2）选择最好的策略处理查询MRQ。这个策略用一个偶对表（F，S）描述，即将数据片F传送到节点S去处理。（3.3）则将所有指定的数据片传送到其处理节点。最后，（3.4）执行查询MRQ。如果还有子查询存在，则算法返回Step 3，实施下一个循环，否则就终止。

注意：真正的优化是在（3.1）和（3.2）实施的。

分布INGRES算法的特点是有限搜索解决方案空间，在每一步找出最佳决策，而不考虑整个全局优化中的后继步骤。

2.分布System R*算法

分布System R*查询优化算法是System R查询优化算法的扩展。因此，对所有可选策略穷尽搜索，从而选出开销最小的一个。虽然这些策略的预测与估价耗费颇大，但是，如果这个查询的执行频度较高的话，这种管理开销还是可以容忍的。

分布System R*查询优化算法是以关系为单位的。在分布System R*中，查询启动的节点称为主节点。主节点上的优化器负责做出所有节点的决策，如选择执行节点和传输数据的方法。查询中的其他节点称为从属节点，负责实施剩下的查询本地存取计划。System R*算法的目标函数是总开销，包括本地处理和通信开销。

下面是R*查询优化算法，其输入是定位后的查询，如关系代数树、关系定位及其统计信息。

算法7.4 QP-R*

像集中式情况一样，优化器必须选择连接序、连接算法（嵌套循环或归并连接）和每个数据片的存取方法（如聚集索引（clustered index）、顺序扫描（sequential scan）等）。这些决策是基于统计信息、中间关系估算公式和存取路径信息的。此外，优化器必须选择连接结果节点和节点间传输数据的方法。

System R*里，主要有两种方法支持节点间的数据传输。

●整体传输（ship-whole）：整个关系送到连接节点，在连接前存放在临时关系里。如果连接算法选取归并连接，则无需存放关系，连接节点以流水线方式在其到达时处理到达的元组。

●按需取用（fetch-as-needed）：顺序扫描外关系，每个元组将连接值送到内关系所在节点，选出和连接值匹配的内关系元组，回送到外关系所在节点。该方法等价于内关系和外关系元组的半连接。

显然，整体传输会产生较大的数据传输，但所需传输的消息数目（链路建立数目）要少于按需取用。直观来讲，若关系较小，则采用整体传输比较合适。反之，如果关系较大或连接选择性较好（匹配的元组较少），则采用按需取用更合适。

System R*算法不考虑连接方法的所有可能组合，因为有些方法不值得考虑。例如，在嵌套循环连接算法里使用按需取用传输外关系是不可取的，因为外关系的所有元组都必须处理。

我们来分析一下，令外关系为R，内关系为S，连接属性是A，则有4种连接策略可用。为了简化，我们忽略生成结果的开销。我们再假设s为S和R匹配的平均元组数，则

s=Card（S∝A R）/Card（R）

策略1：将整个外关系传送到内关系所在的节点。

策略2：将整个内关系传送到外关系所在的节点。此时内关系元组不能一送到就和外关系连接，需要先存放在临时关系T里。

策略3：按需为外关系的每个元组从内关系取元组。此时，对于R中的每个元组，其连接属性值传送到S所在的节点。然后将与这些连接属性值匹配的S里的s个元组选出来发送到R所在的节点，一传到就实施连接。

策略4：将两个关系都传送到第三方节点并计算连接。此时，内关系先传送到该节点，所以先存放在临时关系T里。然后外关系传送到第三方节点，一到就和T连接。

结合两种数据传输方法，可以产生多种情况。下面小结几种典型情况。

（1）嵌套循环（nested-loop），外关系整体传输，但不存储，其开销为：

C1=C（nested-loop）+Cmes×Card（O）×Size（O）/m^[4]

其中：Cmes为发送一条消息的单位成本；M为发送每条消息的大小（字节计）。

（2）归并扫描（merge-scan），外关系整体传输，但不存储，其开销为：

C2=C（merge-scan）+Cmes×Card（O）×Size（O）/m

（3）嵌套循环，内关系按需取用：

C3=C（nested-loop）+Cmes×Card（O）×（1+NI×Size（I）/m）^[5]

（4）归并扫描，内关系按需取用：

C4=C（merge-scan）+Cmes×val（A［O］）×（1+NI×Size（I）/m）

（5）归并扫描，内关系整体传输，先存储再使用：

C5=C（merge-scan）+Cmes Card（I）×Size（I）/m+2×NI×CI/O

【例7.22】 考虑查询外关系PROJ和内关系EMP_PROJ的连接，连接属性是PNO。假设PROJ和EMP_PROJ存放在两个不同的节点上，EMP_PROJ在PNO上有一个索引，可能的执行策略如下。

（1）将整个PROJ传送到EMP_PROJ所在的节点。

（2）将整个EMP_PROJ传送到PROJ所在的节点。

（3）按需为PROJ的每个元组取EMP_PROJ的元组。

（4）将EMP_PROJ和PROJ传送到第三方的节点。

System R*算法预测每个策略中的时间，选出其中最短的一个。如果PROJ∞EMP_PROJ连接之后无其他操作了，则显然策略4的开销最大。如果Size（PROJ）远大于Size（EMP_PROJ），则策略2的通信时间最短；如果其本地处理时间与策略1和策略3的相比不是大很多的话，则策略2为最佳。值得一提的是，这里策略1和策略3的本地处理时间可能比策略2的短很多，因为可以使用连接属性的索引。

若策略2不是最佳，则可从策略1和策略3中选择。这两个策略的本地处理时间是不一样的。若PROJ较大或EMP_PROJ中只有不多元组匹配，策略3通信时间最短，则为最佳。否则，如果PROJ小或EMP_PROJ中匹配元组较多，则策略1为最佳。

3.SDD-1算法

SDD-1算法起源于爬山算法。爬山（hill-climbing）算法是一种贪心算法（greedy algorithms），特点是先从易取得的解决方案开始，然后不断地改进它。其主要问题是初始开销较大。进一步，不一定能收敛到全局最小结果。

在SDD-1算法中使用了半连接，爬山算法得到了进一步改进。目标函数依据总的通信时间（不考虑本地处理时间和响应时间）。最后，该算法使用数据库的统计信息即数据库概貌（database profiles）。此外，该算法使用后优化步骤以改进所选解决方案。该算法的主要步骤是确定有益的半连接，并进行排序。

半连接成本是连接属性A的传输，为：

Cost（R∝A S）=T MSG+TTR*Size（∏A（S））

忽略T MSG，则可以看作开销和传输数据量成正比。

半连接收益是使用该半连接使得可以减少关系R元组传输的开销：

Benefit（R∝A S）=（1-ρ）*Size（R）*T TR

SDD-1算法处理分为四个阶段：初始化、选择有益半连接、选择数据汇聚节点和后优化。该算法的输出是执行这个查询的全局策略，是查询执行的全局计划（见图7.24）。

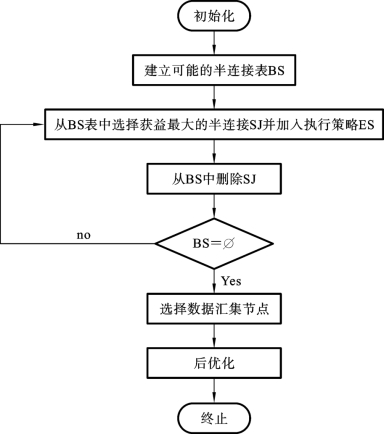
图7.24　SDD-1优化算法示意

算法7.5 QP_SDD-1

初始化阶段是生成一个有益半连接集合BS=｛SJ1，SJ2，…，SJk｝和一个只包含本地处理的执行策略。第二阶段是采用迭代方式从BS里选择有益半连接，每次选出最佳的半连接SJi。然后假设该半连接实施后的结果，修改数据库统计信息和BS。这种修改对该半连接涉及的关系的统计数据进行修改，也修改BS中剩下的使用该关系的半连接的统计数据。重复这个过程，直到没有剩下的半连接的收益高于开销为止。

第三阶段是选择数据汇集节点，分析每个候选节点，计算用其收集数据时的传输开销，选出其中最小传输链的一个节点作为汇集节点。

第四阶段是后优化阶段。在最后阶段，若有半连接会影响汇集节点上的关系的半连接，则从前面定下的方案中删除它。此外，若有半连接，可以将其操作数用其他半连接约简结果取代。

【例7.23】 有如下查询：(www.chuimin.cn)

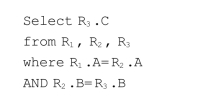
其连接图如图7.25所示。

这三个的关系概貌和属性概貌分别如表7.9、表7.10所示。

图7.25　例7.23的连接图

表7.9　关系概貌

表7.10　属性概貌

①这里ρ为选择系数，可表示为ρ=Val［A］/domain（A），例如Val［R1.A］=30，domain（R1.A）=100，则ρ=0.3。
②累计属性值字节数。

假设T MSG=0，T TR=1，则初始半连接集如下。

SJ1：R2∝R1，其收益是2100=（1-0.3）*3000，成本是36。

SJ2：R2∝R3，其收益是1800=（1-0.4）*3000，成本是80。

SJ3：R1∝R2，其收益是300=（1-0.8）*1500，成本是320。

SJ4：R3∝R2，其收益是0，成本是400。

第一次迭代中，选出的最合适半连接是SJ1，将之加入执行策略ES。其对统计数据的影响是将R2的大小变成900=3000*0.3。进一步，R2.A的选择性也减小，因为半连接后的关系R2（记作R2）的基Card（R2）减小了。新的选择系数记作ρ（R2.A）=0.8*0.3=0.24。最后，R2.A的大小变为96=320*0.3。

第二个迭代里，有两个有益半连接：

SJ2：R2∝R3，其收益是540=900*（1-0.4），成本是200。

SJ3：R1∝R2，其收益是1140=（1-0.24）*1500，成本是96。

最有益的半连接是SJ3，将之加入执行策略ES。对关系R1的影响是，其大小变为360=（1500*0.24）。

第三次迭代里，只剩下一个有益的半连接SJ2，将之加入执行策略ES。其目的是减小关系R2的大小，为360=900*0.4，其统计信息也随着改变。

约简后，存放在Site1的数据量是360，Site2的数据量是360，Site3的数据量是2000。因此Site3选为数据汇集地点。后优化无法减少半连接，因为ES里的所有半连接都是有益的。结果选出的策略是发送Send（R2∝R1）∝R3和R1∝R2到Site3，该节点作为结果计算节点。

【例7.24】 考虑和分析如图7.26所示的连接图。

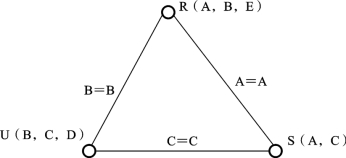
图7.26　连接图

这里涉及三个关系，它们的概况信息如下。

R：Card=5000，Site=1

S：Card=20，Site=2

U：Card=100，Site=3

如果使用半连接技术进行优化，结果会如何？

下面先列出可能的半连接，如表7.11所示。

表7.11　6个可能的半连接

①连接属性是B，Val［R.B］=50，Val［U.B］=20，故ρ=20/50。
②连接属性是A，Val［R.A］=100，Val［S.A］=20，故ρ=20/100。
③连接属性是C，Val［U.C］=10，Val［S.C］=5，故ρ=5/10。

从表7.11可知，选择获利最大的半连接先实施，即P2最先实施。原因是其收益为128000，开销为60，相抵后获益128000-60=127940，最多。P2先实施后，还剩下5个可选半连接。而这个操作会对其他半连接的选择系数、收益及开销发生影响，影响的关系是R。由于S在连接属性（A）上的选择系数很小（0.2），所以半连接后会传递到R的相应属性（A）上，从而使R的基发生变化，细节如下：

Card（R）=0.2*5000=1000

另外，非连接属性也会发生变化，我们可以用前面的估算公式来估算，结果如下。

R：Card（R）=0.2*5000=1000

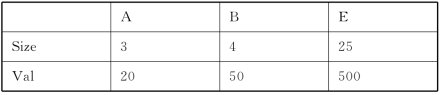
注意：A属性的不同值个数的选择系数从100变成了20。属性B和E不是连接属性，其不同值个数只能依靠估算公式：C（n，m，r），n=5000，r=1000，m（B）=50，m（E）=500。实施后得出剩下的5个半连接如表7.12所示。

表7.12　剩下的5个半连接

由表7.12可知，这5个半连接里，获益最大的是P1，实施后对R的影响如下。

Card（R）=0.4*1000=400

对非连接属性的影响用估算公式，得出：

n=1000，r=400，m（B）=20，m（D）=100

结果如下。

R：Card（R）=0.4*1000=400

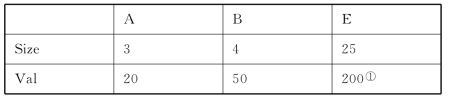
①Card（R）=0.4*1000=400，假设E均匀分布，则Val［R.E］=0.4*500=200。

实施后得出剩下的4个半连接如表7.13所示。

表7.13　剩下的4个半连接

剩下的半连接里，获益最大的为P4。实施结果对U的影响为：

Card（U）=0.5*100=50

对非连接属性的影响用估算公式，得出：

n=100，r=50，m（B）=20，m（D）=100

结果如下。

U：Card（U）=0.5*100=50

实施后得出剩下的3个半连接如表7.14所示。

表7.14　剩下的3个半连接

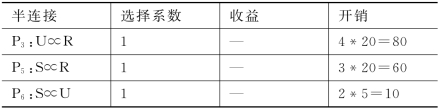
以上三个半连接只有开销，没有收益，因此递归终止。

半连接执行情况如下：

P2→P1→P4

下一步是确定半连接后的数据汇集节点，我们可以将开销计算如下：

Cost（Site1）=（3+2）*20+（4+2+20）*50=1400 （传送约简后的S和U）

Cost（Site2）=（3+4+25）*400+（4+2+20）*50=14100 （传送约简后的R和U）

Cost（Site3）=（3+4+25）*400+（3+2）*20=12900 （传送约简后的R和S）

所以，确定Site1作为汇集节点收集数据。

（后优化略）