优化查询和连接顺序的技巧及方法

本节讨论集中式数据库系统里的查询优化问题，这很有意义。首先，分布式查询要翻译成本地查询，每个本地查询其实就是一个集中式查询。其次，分布式查询优化技术是集中式查询优化技术的扩展。然后，集中式查询优化相对来说比较简单，我们可以先易后难来讨论问题。

下面以两个真实的系统为例，介绍两种不同的查询优化算法：INGRES使用的是动态优化算法；System R使用的是静态优化算法，为一个穷举搜索算法。

1.INGRES的算法

INGRES系统^[3]使用动态优化算法将一个演算递归地分割成更小片段。INGRES系统组合了两个阶段：演算代数分解和优化。具体来说，查询首先分解成查询序列，每个查询包含一个关系（涉及唯一的元组变量）。每个单关系查询由单变量查询处理器（one-variable query processor，OVQP）来处理。OVQP优化处理单一关系时可考虑选择谓词、存取方法（索引、顺序扫描等）等因素。例如：如果谓词形态为〈A=value〉，其中A表示一个属性，就可以使用A上的索引。如果谓词的形态为〈A≠value〉，使用A上的索引已无济于事，此时就需要使用顺序扫描来处理。

这里采用先执行单关系操作的策略，以减少中间关系。

下面假设查询Q分解成两个子序列，分别记作Qi-1和Qi，用Qi-1→Qi表示Qi-1在Qi之前执行，前者的结果为后者使用（即前者的结果为后者的输入）。如果给定一个n元关系上的Q，那么INGRES查询处理器将Q分解为n个子序列Q1→Q2→…→Qn。这个分解使用了两种基本技术：分离（detachment）和替代（substitution）。

分离是查询处理器使用的第一种技术，它将查询Q分解成在一个公共关系上的序列Q′→Q″，它们在同一关系上操作，且Q″使用Q′的结果。

【例7.19】 假设有如下查询，请找出那些在e-Commerce项目工作的雇员的姓名。

Q1：Select EMP.ename

f rom EMP，EMP_PROJ，PROJ

where EMP.eno=EMP_PROJ.eno

AND EMP_PROJ.pno=PROJ.pno

AND pname="e-Commerce"

选择分离后，查询Q1可用Q11来替代，其后继是Q′，这里的TEMP是一个中间关系：

Q11:Select PROJ.pno INTO TEMP

f rom PROJ

where pname="e-Commer ce"

Q':Select EMP.ename

f rom EMP，EMP_PROJ，TEMP

where EMP.eno=EMP_PROJ.eno

AND EMP_PROJ.pno=TEMP.pno

Q′的后继分离可以生成：

Q12:Select EMP_PROJ.eno INTO TEMP'

f rom EMP_PROJ，TEMP

where EMP_PROJ.pno=TEMP.pno

Q13:Select EMP.ename

f rom EMP，TEMP'

where EMP.eno=TEMP'.eno

这样，查询Q1演变成子序列查询Q11→Q12→Q13。查询Q11是单关系的，因此可以由OVQP来处理。但是，Q12和Q13不是单关系的，因此不能用分离技术来约简。

多关系查询无法进一步分离，无法再约简。

定义7.1 查询是不可约简的（irreducible），当且仅当其查询图是由两个节点构成的一个链，或由k个（k＞2）节点构成的圈时。

可以通过元组替换将不可约简查询转换成单关系查询。具体方法是：首先从Q中选出一个关系进行元组替换。令R1为这个关系，对R1中的每个元组t1i，Q中涉及的属性在t1i里用实际值替代，Q变成一个用n-1元关系表示的Q′。因此元组替代产生的查询Q′的总数是Card（R1）。元组替代可以小结为：递归地将Q（R1，R2，…，Rn）替换成｛Q′（t1i，R2，R3，…，Rn），t1i∈R1｝。

【例7.20】 考虑如下查询：

Q13:Se l ec t EMP.ename

f rom EMP，TEMP'

where EMP.eno=TEMP'.eno

这里，变量TEMP′定义的关系落在属性eno上。假设这个关系只有两个元组〈E1〉和〈E2〉，则TEMP′替换生成的两个单关系查询如下：

Q131:Selec t EMP.ename

f rom EMP

where EMP.eno="E1"

Q132:Se l ec t EMP.ename

f rom EMP

where EMP.eno="E2"

以上查询可以由OVQP进行处理。

以上查询的算法可用下面的算法7.1来描述。这个算法递归处理查询，直到没有非单关系查询存在为止。该算法试图应用选择运算和投影运算尽可能快地分离。单关系查询存放在特定的数据结构里，留待随后查询（如连接）的优化和OVQP使用。不可约简查询则通过元组替代来分离。

算法7.1 QP_INGRES。

2.System R的算法

IBM公司研发的System R基于解决空间上的穷举搜索，实施静态查询优化。不像INGRES的算法，System R的算法并不先执行选择运算。

System R优化器的输入是一棵从SQL查询分解而得的关系代数树，输出则是执行“最佳”关系代数树的实施。System R优化器依据时间为每棵候选树赋予一个成本值，保留其中最小的成本值。候选树则通过使用交换律和结合律对n元关系的连接序进行交换后获得。

候选策略是I/O和CPU开销（以时间计）的加权组合。这些开销的估算（在编译期间）基于成本模型，即为低级运算提供的成本公式。对大多数操作来说（除精确匹配选择外），这些公式是基于操作数的基。存放在数据库里关系的基的信息可以从数据库统计来获取，并由System R来管理。

System R的算法是基于连接的。它将连接涉及的两个关系分为内关系（inner relation）和外关系（outer relation），分别记作I和O。

下面给出一些符号，便于以后讨论。

Card（I）：内关系的基数。(www.chuimin.cn)

Card（O）：外关系的基数。

Nout：读外关系所涉及的页面数。

Nin：读内关系所涉及的页面数。

CI/O：读一页的I/O开销。

CCPU：处理一个记录的CPU开销。

System R的优化算法主要包含两步：第一步，基于选择谓词预测每个关系的最好存取方法（成本最小）。第二步，对每个关系R，使用最好的单关系存取方法，再估算最好的连接序。价最廉的序变成最佳执行计划的基础。

考虑连接时，对参与连接的两个关系来说，一个关系称为外关系，另一个关系称为内关系。就像程序设计时的双层嵌套循环一样，外关系是外循环，首先访问；内关系是内循环，外关系的基有多少，内关系的循环次数就有多少。

这样，实现连接运算的方法可以分为嵌套循环和归并连接两种。第一种方法称为嵌套循环（nested loops），对外关系的每个元组，遍历搜索内关系的元组，将匹配的找出来，构成结果关系（记作result）。对内关系来说，连接属性上的索引是非常有效的存取路径。如果没有索引，当两个关系分别为n1和n2个页面，当算法的开销近似于n1*n2，当n1和n2很大时，则是难以接受的。

第一种方法的开销可以描述（顺序扫描外关系O）如下：

C（nested-loop）=（Nout+Card（O）×Nin）×CI/O+Card（Result）×CCPU

第二种方法称为归并连接（merge join），或称归并扫描（merge-scan），把参与连接的两个关系先按连接属性排序。连接属性上的索引可以用作存取路径。如果只有一个关系或没有一个关系被排好序，嵌套循环算法的成本可以和归并连接及排序的成本进行比较。

n个页面排序的成本是n log n。一般在大关系时，使用排序和归并连接算法是合适的。

第二种方法的开销可以描述（先排序再比较）如下：

C（merge-scan）=（Nout+Nin）×CI/O+Csort（I）+Csort（O）+Card（Result）×CCPU

System R的算法的简化版可用下面的算法7.2描述。这个算法里有两个循环，第一个是为查询里出现的每个关系选择最佳单关系存取方法，第二个检查所有可能的连接序（n个关系有n！种可能）。

算法7.2 QP_System R。

3.分片的连接定序

讨论分布式数据库系统的查询优化会涉及数据分片。在分布式环境下，数据片连接定序问题更重要，因为要涉及数据传输通信开销问题。我们将从两个方面来讨论，一是基于半连接的算法，一是非基于半连接的算法。

有些优化算法直接使用连接来优化定序，有些使用半连接来优化定序。分布式INGRESS和System R*的算法是典型的非基于半连接的算法。

首先考虑一些主要假设。我们不再明显区分数据片或关系，同时忽略本地处理时间，并假设一元关系运算（选择与投影）已处理完。因此，这里我们只考虑连接运算，假设其操作数关系放在不同的节点，我们再假设关系的传输是一次一个集合而非一次一个元组来实施的。

下面考察单连接的情况。令该查询为R∞S，R和S是存放在不同网络节点上的关系。要传输的关系的选择是依据参与关系的大小，选小的关系进行传输，将大的关系的所在地作为受方，如图7.22所示。为此，先要估算R和S这两个关系的大小。要注意的是，中间关系的大小也是一个重要因素，但要估算准确很不容易。这里，一种解决方案是把所有策略的通信开销作为参考标准。

【例7.21】 令查询的一元运算实施后剩下的连接操作是PROJ∞pno EMP∞eno EMP_PROJ，如图7.23所示。这几个关系分别存放在Site1（存放EMP）、Site2（存放EMP_PROJ）和Site3（存放PROJ）中。

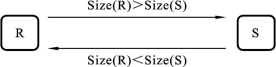
图7.22　选小的关系传输

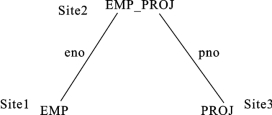
图7.23　分布查询的连接图

下面来看一些执行策略。

策略1：EMP→Site2，在Site2计算EMP_PROJ=EMP∞EMP_PROJ；EMP_PROJ→Site3，在Site3计算EMP_PROJ∞PROJ。

策略2：EMP_PROJ→Site1，在Site1计算EMP_PROJ=EMP∞EMP_PROJ；EMP_PROJ→Site3，在Site3计算EMP_PROJ∞PROJ。

策略3：EMP_PROJ→Site3，在Site3计算EMP_PROJ=EMP_PROJ∞PROJ；EMP_PROJ→Site1，在Site1计算EMP_PROJ∞EMP。

策略4：PROJ→Site2，在Site2计算PROJ=PROJ∞EMP_PROJ；PROJ→Site1，在Site1计算PROJ∞EMP。

策略5：EMP→Site2，PROJ→Site2，在Site2计算EMP∞PROJ∞EMP_PROJ。

为了从中选出一个，必须估算出Size（EMP）、Size（EMP_PROJ）、Size（PROJ）、Size（EMP∞EMP_PROJ）和Size（EMP_PROJ∞PROJ）等的大小。进一步，如果主要考虑响应时间，则可以考虑并行处理的策略5。

4.基于半连接算法

基于连接算法的缺点是必须整关系地在节点间传输。为了克服这个不足，可以考虑用半连接作为约简器，将参与连接的关系缩小。

假设分别存放在Site1和Site2上的两个关系R和S在属性A上连接，则可有以下三种半连接策略。

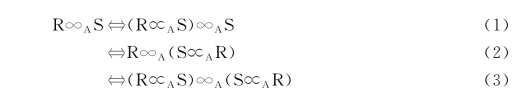
选择上述三种半连接策略中的一种需要估算各自的相关开销。

具体来说，使用策略1半连接的过程如下。

Step 1：∏A（S）→Site1

Step 2：在Site1计算R=R∝A S

Step 3：R→Site2

Step 4：在Site2计算R∞A S

为了简化，我们忽略通信时间里的常数TMSG，因为TTR*Size（R）要比T MSG大得多。借助传输数据量，我们可以比较不同的算法。基于连接算法的开销是将关系R传到Site2。基于半连接算法的开销是上面Step 1、Step 3的开销。因此，使用半连接算法的优势条件如下：

Size（∏A（S））+Size（R∝A S）＜Size（R）

我们来看图7.22，可以用半连接来代替连接EMP∞EMP_PROJ∞PROJ，结果为EMP∞EMP_PROJ∞PROJ，其中，EMP=EMP∝EMP_PROJ和EMP_PROJ=EMP_PROJ∝PROJ。

其实，我们可以用两个半连接作为约简器来约简EMP的大小：

EMP=EMP∝（EMP_PROJ∝PROJ）

因为若Size（EMP_PROJ∝PROJ）≤Size（EMP_PROJ），则Size（EMP）≤Size（EMP）。这样EMP可以约简为EMP∝（EMP_PROJ∝PROJ）。

对于一个给定关系，可用多个半连接来约简。那么，先选哪个半连接成了又一个优化问题。一种常用的方法是比较开销和获益后选择最划算先做。所有约简计划中，如果能找出一个最佳的半连接程序，则称为全约简器（full reducer）。所以，需要估算出约简的大小和需要的开销。注意，这里会有两类特殊情况出现。

（1）一类查询构成的图为一个环，在环里探索实施半连接，循环探索，不收敛，不存在全约简器。

（2）另一类查询构成的图是无环的，称为树状查询，其中存在全约简器。但是候选半连接的数目随着连接数的增长呈指数增长，算法的复杂性成了关键，因为这是一个NP-hard问题。