两个关系表达式E1和E2是等价的，可记作E1≡E2。常用的等价变换规则有以下几种。，Bm是E2的属性，则：10.投影与并的交换若E1和E2为可比属性，则有......
2023-11-24
等价变换原理及规律-分布式数据库技术
【摘要】：下面这两个查询是等价变换：那么它们为何等价？下面讨论关系代数的等价变换规律，基础是我们在代数中常用的交换律、结合律、分配律等。，An）注意，这是有条件的，具体条件在表7.1中说明。表7.1是一元运算交换律的情况。表7.1一元运算的交换律其中：√表示这个交换律是成立的，表示这个交换律是不成立的。表7.2二元运算的交换律和结合律注：PreCon1：∞F2 T→R∞F1：AttrAttr∪Attr。表7.3幂等律4.分配律分配律如表7.4所示。
什么是等价变换？我们先来看一个例子。【例7.5】 下面这两个查询是等价变换：
那么它们为何等价？为何要等价才可变换？下面讨论关系代数的等价变换规律，基础是我们在代数中常用的交换律、结合律、分配律等。
一元运算的交换律，可记为（下面用U表示一元运算，如选择和投影）：U1 U2 R↔U2 U1 R。
二元运算的交换律，可记为（下面用B表示二元运算，如连接、并等）：R B S↔S B R。
结合律可记为：R B（S B T）↔（R B S）B T。
幂等律可记为：U R↔U1 U2 R。
分配律可记为：U（R B S）→U（R）B U（S）。
因式分解可记为：U（R）B U（S）→U（R B S）。
下面假设有两个关系R和S，其中R定义在属性A=｛A 1，A 2，…，An｝上，S定义在属性B=｛B1，B2，…，Bn｝上，那么：
●二元算符的交换律，例如R和S的笛卡儿积是满足交换律的：R×S↔S×R
两个关系的连接也是满足交换律的：R∞S↔S∞R
●二元算符的结合律，例如笛卡儿积和连接运算是满足结合律的，即
（R×S）×T↔R×（S×T）
（R∞S）∞T↔R∞（S∞T）
●一元运算的幂等律。同一关系上的几个投影操作可以组合起来；反之，几个属性上的一个投影可以分解成几个投影的操作序列，即
令R定义在属性集A上，且A⊆A，A⊆A和A⊆A，则
ΠA′（ΠA″（R））↔ΠA′（R）
令σFi（Ai）为同一关系上的子序列选择，其中Fi是应用于属性Ai上的谓词，则
σF1（A1）（σF2（A2）（R））=σF1（A1）∧F2（A2）（R）
反之，由合取谓词标识的简单选择可以分成几个子序列查询。
●交换投影运算和选择操作运算，结果为：
ΠA1，…，An（σF（Ap）（R））↔σF（Ap）（ΠA1，…，An（R））
注意，这是有条件的，具体条件在表7.1中说明。
●交换选择运算和二元运算。
选择运算和笛卡儿积运算的交换结果为：
σF（Ai）（R×S）↔（σF（Ai）（R））×S
注意，这里假设Ai是关系R的属性集A的子集。
选择运算和连接运算的交换结果为：
σF（Ai）（R∞F（Aj，Bk）S）↔σF（Ai）（R）∞F（Aj，Bk）S
选择运算和并运算的交换（假设关系R和T是兼容的，即有相同的关系模式）为：
σF（Ai）（R∪T）↔σF（Ai）（R）∪σF（Ai）（T）
选择运算和差运算也同样可交换。
●交换投影运算和二元运算。
投影运算和笛卡儿积运算是可以交换的，但要满足条件，C=A∪B，其中A⊆A，B⊆B，A和B是关系R和S上的属性集：
ΠC（R×S）↔ΠA（R）×ΠB（S）
投影运算和连接运算也是可交换的，其结果为：但要满足一定的条件，Ai∈A，Bj∈B，详见请见表7.4和表7.5。
ΠC（R∞F S）⇒ΠA（R）∞FΠB（S）
投影运算和并运算的交换结果为：
ΠC（R∪S）↔ΠC（R）∪ΠC（S）
投影运算和差运算也是可交换的。
1.一元运算的交换律
一元运算是只有一个操作对象的操作。本节研究何种情况下交换律是成立的。表7.1是一元运算交换律的情况。
表7.1 一元运算的交换律
其中：√表示这个交换律是成立的，⊗表示这个交换律是不成立的。有时在有条件时成立，我们把前提条件记为PreCon，用下标来区分不同的前提条件。令Attr（）为一个函数，表示抽取变量里涉及的属性集，这样，表7.1中的两个前提条件如下：
PreCon1：Attr（F2）⊆A 1
PreCon2：A1≡A2
其中：Attr（F2）表示F2中涉及的属性集。
这两个前提条件分别表示：PreCon1为一个先选择后投影的运算可交换，当且仅当先执行的选择谓词涉及的属性集包含在投影的目标属性集中（否则，交换后变为后选择运算，由于其选择谓词涉及的属性集不存在而无法执行，从而交换前后的结果不等价）；PreCon2为两个投影运算可交换，当且仅当这两个投影运算的目标属性集相同。
2.二元运算的交换律和结合律
二元运算在这里指的是并、差、积、连接和半连接。
表7.2中的第二行描述的是二元运算的交换律，显然并运算、笛卡儿积运算和连接运算是可交换的，而差运算和半连接运算不满足交换律。第三行描述的是二元运算的结合律，并运算和笛卡儿积运算满足结合律；差运算和半连接运算不满足结合律；连接运算则在有条件时满足结合律，条件是如果两个连接运算满足结合律，则原来排序在后面执行的连接运算的限定谓词涉及的属性集要处在两个连接运算限定谓词的交集里，否则交换后由于缺少连接属性而使得最后执行的连接无法实施。
表7.2 二元运算的交换律和结合律
注：PreCon1：（R∞F1 S）∞F2 T→R∞F1（S∞F2 T）：Attr（F2）⊆Attr（S）∪Attr（T）。
3.幂等律
幂等律指的是一元运算的性质。投影运算和选择运算都满足幂等律，但一个一元运算拆解成两个一元运算时需满足前提条件，即PreCon。对投影（∏）而言，满足幂等律的前提条件是A和A 1相同，A 2是A的一个子集。对选择（σ）而言，满足幂等律的前提条件是谓词表达式F是表达式F1和F2的交，如表7.3所示。
表7.3 幂等律
4.分配律
分配律如表7.4所示。由表可知，并运算满足分配律，差运算满足选择运算的分配律，但不满足投影运算的分配律，有条件的笛卡儿积运算满足分配律（前提条件为PreCon1），有条件的连接运算满足分配律。对选择运算而言，其分配的前提条件是PreCon1；对投影运算而言，其分配的前提条件是PreCon2。半连接对选择运算而言满足分配律，有条件的满足投影的分配律（前提条件为PreCon2）。
表7.4 分配律
(www.chuimin.cn)
注：PreCon1：∃FR，FS：（F=FR∧FS）∧（Attr（FR）⊆Attr（R））∧（Attr（FS）⊆Attr（S））；
PreCon2：Attr（F3）⊆A，（AR=A-Attr（S）∧AS=Attr（S）∩Attr（F3））。
这里，PreCon1表示将一个选择运算分解成两个选择运算，则原始选择运算的选择谓词为分解后两个选择运算的选择谓词的交。
PreCon2意味着若一个投影运算分解为前后两个投影运算，则分解后的两个投影运算中的后一个投影运算的投影结果属性集与未分解前投影运算的结果属性集相同，以保证变换前后的结果投影集相同。同时，要求在执行投影运算后，保留连接/半连接条件含有的属性，以便仍能实施连接/半连接。
5.因式分解
因式分解（factorization）如表7.5所示。
表7.5 因式分解
注：PreCon1：FR⇒FS∧FR=F；
PreCon2：Attr（R）=Attr（S），AR=AS=A；
PreCon3：FS=true∧FR=F。
现在来看一棵等价算符树，如图7.3所示。
我们用上述规则进行简化。首先，可以将一元运算进行分解，以简化查询表达式。其次，将同一关系上的一元运算进行组合，使得对一个关系的一元运算可以通过一次存取实现。再次，可以交换某些一元运算与二元运算，让一元运算（如选择运算）先执行。最后，将二元运算进行排序，结果可以用图7.4表示。
【例7.6】 将图7.3所示的等价算符树演变成重写后的算符树（见图7.4）。
图7.3 等价算符树
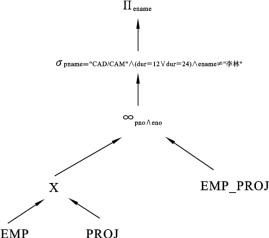
图7.4 重写后的算符树
重写后的算符树简洁了很多，显然，优化是有效的。
6.等价变换优化
例7.6优化的基础是等价变换。下面对查询的等价变换进行深入讨论。
根据上面的讨论，我们总结目前得到的优化规则如下。
优化规则1：使用选择运算和投影运算的幂等律将每个操作关系生成合适的选择和投影操作。因为一元运算会缩减关系的大小，所以可以先做，使得运算的中间关系变小，这样就有了优化规则2。
优化规则2：在一棵算符树中，尽量将选择运算和投影运算往树叶方向移动。
【例7.7】 假设有一个查询，可以记为：
查询：∏snumσarea=North（SUPPLY∞deptno=deptno DEPT）
表示将供应（SUPPLY）和部门（DEPT）两个关系连接后，选出负责北区（area=North）的供应数据，最后投影到相关的供应商号（snum）上。
这个查询可用图7.5表示。
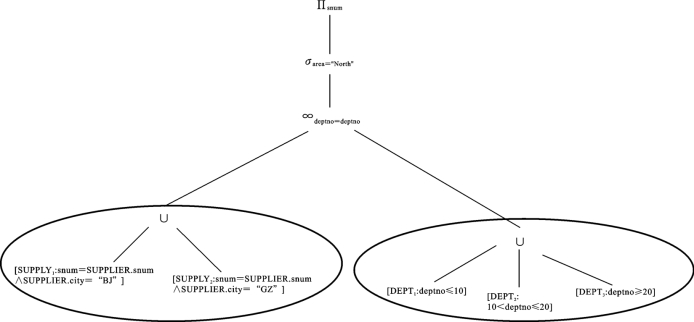
图7.5 例7.7中查询的原始形态
由图7.5可知，假设SUPPLY关系是水平分布的，分成南北两片，一片以北京为核心，一片以广州为核心，即分片谓词分别为city=BJ和city=GZ。在实施操作时，这两个数据片通过并运算重构，因此形成图7.5所示的左面子树。同时，关系DEPT按部门水平分片为三部分，部门号小于等于10的部门为一片、部门号在11～20之间的为第二片，其余为第三片，其重构也由并运算实现，故形成右面子树。我们分别用椭圆圈出，表示这是由关系重构而产生的操作。
采用查询优化规则1和优化规则2，可以将图7.5所示的查询简化为图7.6所示的形态。
显然，图7.6所示的优化结果比原始查询的优化结果好多了（这里为了简洁，我们把重构省略了）。
7.利用公共子表达式来优化
下面进一步讨论等价变换优化。
【例7.8】 找出工号为288的由负责人领导的部门里工资在3000元及以下的雇员的姓名。这个查询可以看成如下形态：
图7.6 查询的简化形态
∏EMP.name（（EMP∞deptno=deptnoσmgrnum=288 DEPT）-（σSAL＞3000 EMP∞deptno=deptnoσmgrnum=288 DEPT））
（这个例子取自参考文献［1］。当然，虽然这个查询符合逻辑，但可能有些读者也会这样批评，用户为何不把这个查询设计得更好。）
这个查询表示，从工号为288的由负责人领导的部门里去掉工资高于3000元的雇员，然后将结果投影到雇员姓名，就是所求结果。
我们发现，其中有一个公共子表达式，即
EMP∞deptno=deptnoσmgrnum=288 DEPT
图7.7 查询及公共子表达式
我们当然不希望把这个子表达式重复计算两次（这样的开销太大），所以希望加以优化。
一旦确定公共子表达式，这个子表达式就只计算一次，然后将结果作为临时数据存放起来，以便下次使用。还可以使用等价公式将查询进一步简化。查询及公共子表达式如图7.7所示。
为了进一步优化，往往需要进一步等价变换，下面给出一些关系运算等价公式，其证明略。
●R∞R↔R；
●R∪R↔R；
●R-R↔∅；
●R∞σF R↔σF R；
●R∪σF R↔R；
●R-σF R↔σF R；
●（σF1 R）∞（σF2 R）↔σF1∧F2 R；
●（σF1 R）∪（σF2 R）↔σF1∨F2 R；
●（σF1 R）-（σF2 R）↔σF1∧F2 R。
这样可以运用以上公式将这个查询进行优化。
首先找出公共子表达式，然后依据上面的规则进行优化。若令这个公共子表达式的结果为一个临时关系S，则这个查询中的差运算可以表述成：
S-σSAL＞3000 S
依据等价规则R-σF R↔σF R，可以将这个差运算替代掉，结果如图7.8所示。
按照优化规则，图7.8这个形态还可以继续优化，把一元运算尽量往叶子处下推，从而形成图7.9所示的形态。显然，查询结果被大大优化了。
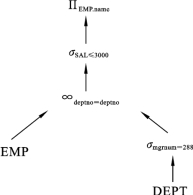
图7.8 对公共子表达式进行优化
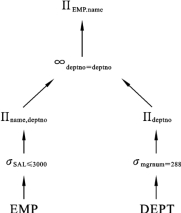
图7.9 进一步优化后的形态
有关分布式数据库技术的文章
- 详细阅读
-
物联网原理及分布式数据库技术详细阅读
进一步说，物联网需要各行各业的参与，是一项综合性的技术，是一项系统工程。物联网的规划、设计和研发，关键在于射频识别、传感器、嵌入式软件以及传输数据计算等领域技术的发展。一般来讲，物联网的主要工作包含以下几方面。互联网将人连接起来，物联网将设备（物）连接起来，物的数量远远大于人。随着越来越多的设施加入物联网，数据大小呈指数级增长。......
2023-10-28
- 详细阅读
- 详细阅读
-
二维傅里叶变换原理及应用详细阅读
由式容易推导出傅里叶变换基矩阵如下：这里假设图像由N×N个元素组成。表5-14 阶傅里叶基本图像指数由式可得到傅里叶基本图像见表5-1。需要指出的是，傅里叶基本图像都是复图像。图5-34 阶傅里叶基本图像由图5-3可以看出，实部和虚部相位差是π/2，对于4阶傅里叶变换的空间单位频率是2π/4，即实部和虚部按隔行或隔列对准。......
2023-06-23
-
的原理及应用光伏系统中变换器的原理及应用详细阅读
光伏发电系统通常分为独立发电系统和并网发电系统。独立光伏发电系统是孤立的发电系统，主要应用于偏远地区。因而光伏并网发电系统可作为分布式能源发电系统的一种有益补充。图5-14给出了典型光伏并网发电系统的结构示意图。图示光伏发电系统中的变换器包括光伏直流电压升压变换器、蓄电池充电控制器、、DC/AC逆变器等。在光伏发电系统用变换器中，光伏并网逆变器是整个光伏并网发电的核心。......
2023-06-23
-
矩阵初等变换、初等矩阵与等价矩阵解析详细阅读
【主要内容】1.矩阵的初等变换矩阵的下列三种变换称为矩阵的初等行（列）变换：（1）互换矩阵的两行（两列）.（2）用一个非零常数c乘矩阵的某行（某列），即用c乘某行（某列）的每个元素.（3）矩阵某行（某列）的k倍加到另一行（另一列），即某行（某列）的每个元素的k倍，加到另一行（另一列）的对应元素.矩阵的初等行变换与初等列变换，总称矩阵的初等变换.2.初等矩阵单位矩阵经过一次初等变换所得到的矩阵，称为......
2023-10-27
-
矩阵初等变换及相抵定理原理介绍详细阅读
初等变换对于矩阵来说是最重要的运算.初等变换到底改变了什么呢？，Ps，Q1，Q2，…，Qt，满足条件P=P1P2…Qt.因此，我们可以得到关系式P1P2…Qt=B. 由命题3.2得到，式就表明，矩阵A可以通过一系列的行与列的初等变换化为矩阵B.证毕.定理3.4m×n阶矩阵A必可相抵于一个形如的矩阵，该矩阵中除了a11，a22，…......
2023-11-22
相关推荐