查询优化器体系结构：分布式数据库技术解析

2023-10-28 理论教育版权反馈

【摘要】：查询优化器体系结构如图6.2所示。图6.2查询优化器体系结构查询优化器的工作过程一般分为两个阶段：重写阶段和规划阶段。在集中式系统中，查询执行策略可以很好地使用扩展关系代数来表示。集中式查询处理器的主要角色是为给定查询根据等价原理选择最好的关系代数查询表达形式。同时，除了要选出关系代数运算的顺序外，分布查询处理器还需确定最佳的运算执行节点。

查询优化器体系结构（query optimizer architecture）如图6.2所示。

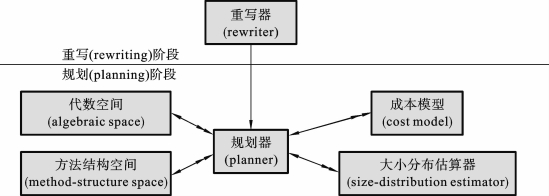
pagenumber_ebook=118,pagenumber_book=103

图6.2　查询优化器体系结构

查询优化器的工作过程一般分为两个阶段：重写（rewriting）阶段和规划（planning）阶段。查询优化器的组成模块包括重写器（rewriter）、规划器（planner）、成本模型（cost model）、大小分布估算器（size-distribution estimator）。

1.重写器

重写器负责将一个给定的查询进行转换，生成更有效的等价查询。例如，将视图用其基关系代替。此时只考虑查询的静态特征，不访问具体的数据，因此，称为是陈述性的（declarative）。

2.规划器

规划器负责为每个查询检查所有（尽量达到所有）可能的执行计划。从中选出最合适的（一般是性价比最高的）计划，用于为用户提出的查询生成答案。由于查询的可实现计划很多，所以需要一个搜索算法搜索整个计划空间。整个计划空间可以分为两部分：代数空间（algebraic space）和方法结构空间（method-structure space）。

（1）代数空间指的是用关系代数表示的操作执行序列，一个查询可以用多种基本代数运算序列表示，代数空间包含所有用于实现用户提出的查询的可能的代数运算序列。

（2）方法结构空间用于描述按代数空间中某个代数运算序列的代数运算执行方法，让规划器选择最佳的实现方法。例如，一个连接（join）运算可以使用两个运算关系实现笛卡儿积运算，再通过选择和投影运算来实现，也可以使用嵌套循环（nested loops）、归并扫描（merge scan）等方法实现（细节请参见后面章节）。

3.成本模型

成本模型用于估算执行计划成本的算术公式。对每个连接方法、每个不同的索引类别存取等都有对应的成本估算公式，估算内容包含CPU开销、存储开销、缓存开销、I/O开销和通信开销等。

4.大小分布估算器

大小分布估算器用于描述数据库关系（字段）及索引大小分布。按不同的应用领域，数据的分布是不同的。例如，性别为二值分布（如取“男”、“女”二值），基本上可以看作是均匀分布的，但在描述军人的关系中，并不是均匀分布的（大多数情况下，男性数目大于女性数目）。在全体人口中，年龄在1～120岁之间是均匀分布的，但在学生关系中，年龄分布基本在6～30岁之间。这对于规划和优化很重要。这里为何是估算而不是实际计算？原因是，在查询优化时尚未真正存取用户数据，优化算法是靠存取数据字典（元数据）来试图获得数据库、关系等的大小及分布信息的。

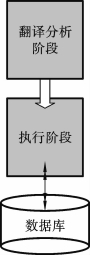
pagenumber_ebook=119,pagenumber_book=104

图6.3　DBMS运行的两个阶段

DBMS运行可分为两个阶段，即翻译分析阶段和执行阶段，如图6.3所示。查询处理则是翻译分析阶段的主要工作。

值得注意的是，对处于翻译分析阶段的查询优化来说，由于此时没有真正存取数据库的数据，其基础只能靠数据字典里的信息和好的算法。

简单来说，关系查询处理器的主要功能是将一个高级查询（典型的是关系演算）转换成一个等价的、低级的查询（典型的是关系代数）。低级查询是实现查询的执行策略。这种变换必须遵循正确性和有效性。如果低级查询的语义和原来的语义相同，并得出相同的结果，我们就说这种变换是正确的。

什么是关系演算？按照网上的说法^[1]：

关系演算有两种演算：元组关系演算和域关系演算，它们是数据库关系模型的一部分，能提供指定数据库查询的声明性方式。

关系代数和关系演算是逻辑等价的：对于任何代数表达式，都有一个等价的演算表达式，反之亦然。

关系演算首先是E.F.Codd于1972年提出的，它包括一个对表进行操作的集合。

●SELECT（σ）：从关系里抽取出满足给定限制条件的元组。

●PROJECT（Π）：从关系里抽取指明的属性（列）。

●PRODUCT（×）：计算两个关系的笛卡儿积。

●UNION（∪）：计算两个表集合理论上的并集。

●INTERSECT（∩）：计算两个表集合理论上的交集。

●DIFFERENCE（-）：计算两个表的差异（区别）的集合。

●JOIN（∞）：通过共同属性连接两个表。

同样的查询，不同的处理方式，结果虽然一样，但是效率却有很大差别。下面看一个例子。

如果有两个关系，它们的关系模式如下：

EMP(eno，ename，t i t l e)

EMP_PROJ(eno，pname，resp，dur)

它们用于描述雇员信息与雇员-项目信息。在关系EMP中，属性为工号（eno）、雇员姓名（ename）和职称（title）。在关系EMP_PROJ中，属性为工号（eno）、项目名（pname）、职责（resp）和工龄（dur）。

如果用户的请求是找出担任项目经理的所有雇员的姓名，则其SQL形式表达如下：

Select ename

f rom EMP，EMP_PROJ(www.chuimin.cn)

where EMP.eno=EMP_PROJ.eno

AND resp="Manager"

【例6.1】这个查询的两个等价的表达式如下：

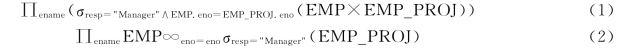
pagenumber_ebook=120,pagenumber_book=105

第一个表达式使用了笛卡儿积。众所周知，笛卡儿积运算消耗的计算资源很多，即复杂性高。第二个表达式避免了EMP和EMP_PROJ的笛卡儿积，因此可以节省很多计算资源。从以上表达式可以看出，在有多种实现查询方案可供选择的情况下，实现方案的优劣差异很大，这样就可显示出查询优化的重要性。

在集中式系统中，查询执行策略可以很好地使用扩展关系代数来表示。集中式查询处理器的主要角色是为给定查询根据等价原理选择最好的关系代数查询表达形式。

在分布式系统中，仅靠关系代数不足以表达执行策略。为了能够在节点之间交换数据，必须补充一些操作（例如，数据发送与数据接收）。同时，除了要选出关系代数运算的顺序外，分布查询处理器还需确定最佳的运算执行节点。这样，选择分布执行策略的难度增加，分布查询处理更困难。

【例6.2】进一步考察例6.1的第二式：

假设关系EMP和EMP_PROJ的水平分布如下。

EMP分为两个数据片：

EMP1=σeno≤3（EMP）

EMP2=σeno＞3（EMP）

EMP_PROJ也分为两个数据片：

EMP_PROJ1=σeno≤3（EMP_PROJ）

EMP_PROJ2=σeno＞3（EMP_PROJ）

假设EMP_PROJ1、EMP_PROJ2、EMP1和EMP2分别存放在节点l、节点2、节点3和节点4上，而这个查询的结果希望放到节点5。

为了便于说明，可以忽略投影操作。我们来看两种不同的策略，进而分析优化的必要性。

例6.2中，该查询的两种等价分布执行策略如图6.4所示。策略1利用EMP和EMP_PROJ分片的特点选择并行实施和连接操作。策略2在处理查询前把所有操作数据集中到需要输出结果的节点。可以看出，策略2是一种平面化的执行策略。

图6.4是使用树的形式来描述查询运算，我们称这类树为算符树或操作树。图6.4（a）所示的策略1中，根表示并运算（∪），其两个分支节点都是连接运算（∞）。以左面的子树为例，其左面子孙为一个数据片EMP1，是叶子；右面是一棵子树，子树根为投影操作σresp=“Manager”。投影子树的子孙为数据片EMP_PROJ1，也是叶子。右面子树的含义类似于左面子树的含义。图6.4（b）所示的策略2中，根为整个查询运算，叶子为操作所需的数据片的所在节点，有向弧上的标示为需传输的数据片，传输的目的地为实施运算的节点。

为了估算这两种策略的资源消耗，我们假设存取1个元组需要1个单位时间，记作tac，令传输1个元组需要10个单位时间，记作ttrans。假设关系EMP和EMP_PROJ分别有400个元组和1000个元组；假设关系EMP_PROJ中有20位经理，数据在节点是均匀分布的；再假设关系EMP_PROJ和EMP各自是按照属性resp和eno聚合的。因此，可以基于resp的值直接访问EMP_PROJ的元组。

策略1的总开销如下。

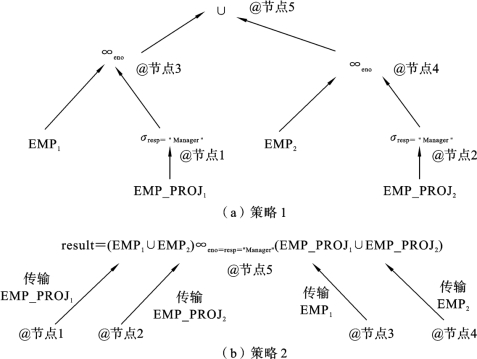
pagenumber_ebook=121,pagenumber_book=106