分布式数据库技术数据分片设计

2023-10-28 理论教育版权反馈

【摘要】：对于数据水平分片，主要考虑数据的逻辑性质，所以我们会考虑分片的谓词、数据的统计性质，例如应用访问数据片的频度。考虑一个关系EMP（雇员）的水平分布。

数据分片设计是在自顶向下数据分布设计中必须解决的一个重要问题，所以我们先讨论数据分片设计（本节的细节内容选自参考文献［1］，有兴趣的读者可查阅参考文献［1］）。

1.为何要分片

从分片的角度看，分片的意义在于可以选择合适的数据分布单位。其实，无论是从实现上看还是从应用上看，关系都不是一个合适的数据分布单位。

首先，应用所见到的往往只是关系的一个子集。因此，定位在应用的存取上，无须将整个关系纳入视野，只需考虑其一个子集即可。所以，把关系的子集作为数据分布单位是自然的事。

其次，如果应用有一个视图定义在指定关系上，但该关系驻留在其他节点上，这时可选用两种不同的处理方式：第一种是把整个关系作为分布单位，只存放在一个节点上；第二种是将它制作成副本放在提出应用的那些节点上。第一种处理方式会造成不必要的异地数据访问；第二种处理方式会由于数据冗余而造成数据更新的麻烦，尽管该应用只涉及这个关系的一部分。假如这里只选择该应用所涉及的那部分关系数据（作为一个数据片）存放，则会有效得多。

最后，如果把一个关系分解成数据片，每个数据片作为一个分布单位，则可允许更多个事务并发执行。除此之外，关系的分片还会典型地导致一个查询的并行执行，即一个查询会分解成若干个作用在数据片上的子查询，它们可以并行执行，提高了并发度和系统的吞吐量。

下面用一个例子加以说明。

【例3.1】设有一个全局关系EMP（雇员），一个重要应用需要了解这个全局关系中哪些雇员参加哪些项目。令雇员所属的部门恰好与分布式数据库存放该部门信息的节点处于同地。应用则可以从网络中的任何一个节点发布，当然，从部门所在的节点查询本部门雇员的概率要大得多。因为雇员按部门分布，而项目又同属于不同的部门，所以要求了解哪些雇员参与哪些项目。这样，最简单的情况是，这个关系的元组可以按雇员工作的部门来组织。

我们进一步考虑垂直分片的情况，假定SAL（工资）和TAX（税费）只为管理类应用所用，而且总是一起使用。这样，SAL和TAX就可以放在同一个垂直分片里。

2.数据水平分片

下面我们讨论数据水平分片的问题。

何谓数据水平分片？如果我们把一个关系看成一张二维表，每行记录每个客观实体，每列描述客观实体的属性。水平分片指的是按水平方向分割这张表，每个分割是这张表的行集的子集。

对于数据水平分片，主要考虑数据的逻辑性质，所以我们会考虑分片的谓词、数据的统计性质，例如应用访问数据片的频度。当然，要协调好数据的逻辑性质和统计性质不是很容易。

3.基本数据水平分片

关系的基本数据水平分片是指按照限定谓词对一个全局关系实施选择运算后所得的结果，这种选择运算必须满足数据的完备性、不相交性和可重构性。

●完备性是指分割后的数据片应当覆盖所有的（关系）数据记录。

●不相交性，即数据片和数据片之间是两两不相交的。

●可重构性是指分割后的数据片可以方便重构成一个全局关系。

令R为一个全局关系，在设计它的数据水平分片时，必须考虑水平分片的性质是按照选择条件对数据库表格进行水平分割的。而选择运算依赖的是以谓词形式出现的选择条件。所以，下面对这样的谓词进行必要的定义。

定义3.1 简单谓词。

一个简单谓词p的谓词形式如下：

p：属性=value。

例如，“年龄=60”就是一个简单谓词。

定义3.2 小项谓词。

简单谓词集合S中的一个小项谓词（minterm predicate）是S中出现的所有谓词的交，这些谓词可以其自然形式出现，也可以其逆出现，其结果表达式均不应是矛盾的。所以：y=∧p*i，满足y≠false，这里p*i=pi或p*i=pi。例如，y=p1∧p2。

假设p是前面提及的关系EMP，令

p1：SEX="male"，

p2：DEPT=1

那么，

y1=p1∧p2，

y2=p1∧p2，

y3=p1∧p2，

y4=p1∧p2都是小项谓词。

结论：一个水平分布数据片满足小项谓词的所有元组的集合。

定义3.3 相关性。

我们称一个简单谓词pi和一个简单谓词集合S是相关的，如果S中至少存在两个小项谓词，则它们之间的差别仅仅是pi本身（即一个小项中，pi是一般值，另一个是pi的逆），而且至少有一个应用会以不同的方式访问与这两个小项谓词对应的数据片。

令S=｛p1，p2，…，pn｝为一个简单谓词的集合，下面定义S的完备性与最小性。

定义3.4

（1）一个简单谓词集合S是完备的，当且仅当属于同一数据片的两个元组被任何一个应用访问的概率是相同的。

（2）如果一个简单谓词集合S中的所有谓词都是相关的，则S是最小的。

如果一个简单谓词按其一般值和其逆查询时导致发布的分布概率差异很大，则我们称其为与S不相关。

【例3.2】考虑一个关系EMP（雇员）的水平分布。首先，假设涉及这个关系的有些重要应用是：了解哪些雇员参加哪些项目。其次，假设涉及这个关系的有些应用在查询哪些雇员是程序员。最后，假设查询哪些雇员是程序员的请求在各节点上发布的分布概率是均衡的。为了简化问题，假设只有两个部门存在，即部门1和部门2。所以DEPT=1等价于DEPT≠2，反之亦然。

根据这些应用，我们可以归纳出两个简单谓词：DEPT=1和JOB=P（programmer，程序员）。如果列出这两个谓词的小项谓词，则它们为

DEPT=1∧JOB="P"

DEPT=1∧JOB≠"P"

DEPT≠1∧JOB="P"

DEPT≠1∧JOB≠"P"

上述所有简单谓词都是相关的。但是，若有一个谓词AGE=20，那它就不是与S相关的简单谓词，因为年龄为20在年龄分布上是一个特殊的专门值。

这样，一个基本水平分片算法（记作H_Frag）可以描述如下。

Begin

初始化：(www.chuimin.cn)

先选一个谓词p1，它能够把R中的元组分成两部分（注意，要考虑至少有一个应用会分别访问这两部分）。

令S=｛p1｝，迭代过程如下。

（1）考虑一个新的谓词pi，它至少把R中的一个数据片分成两部分，并且至少有一个应用会使用不同的方式分别访问这两部分。

令S←S pagenumber_ebook=59,pagenumber_book=44 ｛pi｝，从中删除不相关的谓词。

（2）重复第（1）步，直到集合S的小项分片是完备的。

End

【例3.3】以雇员（EMP）关系为例，令S=∅。首先选择第一个谓词p1：用户有时会查询工资在5000元以上的雇员情况，这时可以令p1为SAL＞5000，即假设程序员的平均工资大于5000元。这个谓词区分了两个雇员集合：工资大于5000元和小于等于5000元的雇员。结果S=｛p1｝=｛SAL＞5000｝。

然后考虑DEPT=1，这个谓词是与S相关的（假设企业一共有两个部门，DEPT=2即DEPT≠1），加入谓词集合S，结果S=｛p1，p2｝=｛SAL＞5000，DEPT=1｝。

最后考虑JOB=P。这个谓词也是相关的，加入谓词集合S，结果S=｛p1，p2，p3｝=｛SAL＞5000，DEPT=1，JOB=P｝。但是在分析小项谓词性质时发现，SAL＞5000使得S不完备（假设企业工资分布从2000元到10万元。工资大于5000元不是一个严格区分两类不同应用的合理谓词，它使得S是不完备的），因此最后获得的集合是S=｛DEPT=1，JOB=P｝。当企业有很多部门时，DEPT=1也会使得S不完备，但这里假设企业只有两个部门，因此S是完备的。

注意，要确定谓词集合是否完备，有时候开销很大，选择所有可能的谓词会耗费我们大量的时间和系统的计算时间，所以建议不要考虑所有的应用，主要考虑重要应用即可。因此我们可以聚焦于以下两点。

（1）关注一些重要应用。

（2）不区分具有相似特征的数据片。

这样，既可以合适地分片，又能满足效率的要求。

4.导出水平分片

一个全局关系R的导出水平分片（derived horizontal fragmentation）与其自己的属性关联，同时又是通过另外一个关系的水平分片推导出来的。导出水平分片的目的是便于数据片之间的连接运算。

首先定义分布连接（distributed join）。分布连接是指水平数据片之间的连接。两个全局关系R和S之间的连接是应用所需求的。在R和S之间连接时，需要比较它们之间的所有元组。这样一个全局关系R的数据片Ri必须与S的所有数据片Sj（j=1，2，…，n）进行比较，而部分连接（partial join）Ri∞Sj很可能是空集。换言之，它们的连接属性是不相交的。

我们可以使用图3.4所示的连接图来表示。连接图（join graph）G可以记作：

G（N，E）其中：节点N代表关系R和S的数据片；边E代表连接运算。

根据数据分片和查询连接的特点，可以将连接图分成几个有特征的连接图。

定义3.5 全连接图（total join graph）：是指如果关系R和S的所有数据片间的可能连接都存在，即属于R的所有节点和属于S的所有节点间全连接。

定义3.6 分隔连接图（partitioned join graph）：是指一个连接图由两个或两个以上不互联的子图构成。

定义3.7 简单连接图（simple join graph）：是指一个连接图是分隔的且每个子图只有一条边。

图3.5是这三类连接图的示意图。

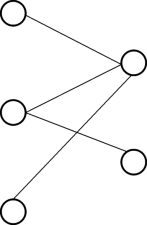
pagenumber_ebook=60,pagenumber_book=45

图3.4　连接图

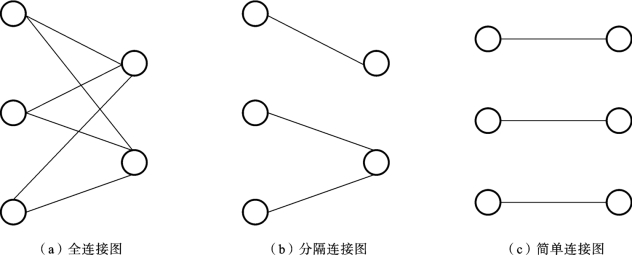
pagenumber_ebook=60,pagenumber_book=45

图3.5　典型连接图

从数据库设计的角度看，让连接变成简单连接图十分重要。这样可使连接运算有的放矢，减少网络上不必要的数据传输，减少不必要的连接运算。

现在考虑一个关系SUPPLY（snum，pno，deptno，quan），用于描述企业中的供应关系，即哪些供应商供应哪些产品。分析应用，发现这个关系经常与其他关系一起使用。确切来说，有些应用需要指定供应商的供应信息，这样需要将SUPPLY和SUPPLIER在属性snum上作连接。还有一些应用要求指定部门的供应情况，所以需要将SUPPLY和DEPT在属性deptno上作连接。

令DEPT按照属性deptno的值作水平分布，SUPPLIER按照属性snum的值作水平分布。这样SUPPLY有两种导出分布的选择，即是与SUPPLIER对应按snum半连接导出分布，还是与DEPT对应按deptno半连接导出分布。最后的决定则取决于应用的频率分布，即是前者的应用频率高还是后者的应用频率高，通常选择应用频率高的来进行设计分布。

5.垂直分片

在垂直分片时要注意，完全的不相交性是无法保证的。至少关系的一个键或者元组标识（tuple identifier，TID）要在不同的数据片里重复，否则无法识别不同数据片之间元组的关联，从而无法重构关系。

垂直分片的目的是能够方便识别一个关系R的数据片Ri，让有些应用只施加在该数据片上。

让我们考虑将一个关系R垂直地分为两个数据片R1和R2。这么做的条件是至少有一个应用会由这种分片而得益，即执行时只涉及其中一个数据片R1或R2，此时我们要避免存取整个关系R。假如有应用要同时访问R1和R2，则需要重新构造R，这是效率最低的。

要指出的是，一个全局关系R的分片算法的复杂性呈指数上升。因此，分片算法常使用启发式算法。

垂直分片一般使用以下两种方式来实施。

（1）分裂方式：这种方式是将一个关系不停地分裂，直到分裂成合理的数据片。

（2）组合方式：这种方式是先把每个属性看作一个垂直数据片，然后逐步归并组合。

这两种方式都可归入贪心启发式方法。它们都试图每次选“最佳”的步骤。但是每个单一步骤最佳不等于总体最佳，所以往往在最后要回溯，回头看看如何来修正和补偿。

垂直分片还会引起数据冗余问题，因为为了数据能重构，数据片中必须有属性重复。重复的结果便利了只读应用，但对更新操作来说，带来了新的复杂度。原因是更新时，每个数据副本都必须更新，否则数据一致性不能保证。

假设两个数据片R1和R2有叠加部分，即存在一个属性集A，其中的属性同时属于R1和R2。令R1和R2分别位于节点1和节点2，则对A中属性的读应用可以就近实现，即如果应用在节点1上发布，则就近读节点1上的数据，在节点2上发布就读节点2上的数据。更新操作就复杂了，必须在所有放置相关属性的节点上完成更新。可见，数据分片时要注意，叠加（即重复）的属性的更新频度要小些。

6.混合分片

我们再来看混合分片的情况。所谓混合分片，指的是既有水平分片又有垂直分片的情况。这里可以有以下两种典型的情况。

（1）先水平分片，然后垂直分片。

（2）先垂直分片，然后水平分片。

需要指出的是，水平分片操作和垂直分片操作是不满足交换律的，即先水平分片再垂直分片与先垂直分片再水平分片（即便水平分片策略与垂直分片策略都不变）的结果是不一样的。

以2.5.4节中的例子Student为例，其分片情况如图3.6所示。

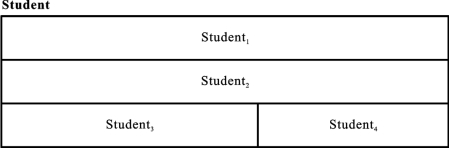
pagenumber_ebook=61,pagenumber_book=46