我们都学习过二元一次方程组，我们一般的解法是消去某个未知数，然后代入求解。例如下面的问题：
我们一般的解法是把①式写成y=5-2x的形式，代入到②式中，消去y，解出x，然后代入解出y。或者将①式等号两边同时乘以2，变成4x＋2y=10，与②式相减，消去y，解出x，然后代入解出y。
这种方法在x、y的系数比较小的时候用起来比较方便，一旦系数变大，计算起来就复杂很多了。下面我们介绍一种更简单的方法。
方法
（1）将方程组写成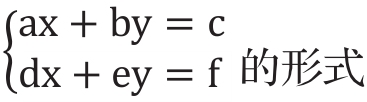
。
（2）将两个式子中x、y的系数交叉相乘，并相减，所得的数作为分母。
（3）将两个式子中x的系数常数交叉相乘，并相减，所得的数作为y的分子。
（4）将两个式子中常数和y的系数交叉相乘，并相减，所得的数作为x的分母。
（5）即x=（ae-db）；y=（ae-db）。
例子
（1）解二元一次方程组
首先计算出x、y的系数交叉相乘的差，即3×2-1×1=5。
再计算出x的系数与常数交叉相乘的差，
即3×10-1×10=20。
最后计算出常数与y的系数交叉相乘的差，
即10×2-10×1=10。
这样x=10÷5=2；y=20÷5=4
所以结果为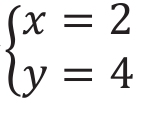
（2）解二元一次方程组
首先计算出x、y的系数交叉相乘的差，即2×2-3×1=1。(www.chuimin.cn)
再计算出x的系数与常数交叉相乘的差，
即2×13-3×8=2。
最后计算出常数与y的系数交叉相乘的差，
即8×2-13×1=3。
这样x=3÷1=3；y=2÷1=2
所以结果为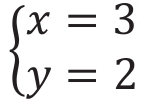
（3）解二元一次方程组
首先计算出x、y的系数交叉相乘的差，
即9×2-7×1=11。
再计算出x的系数与常数交叉相乘的差，
即9×1-7×（-5）=44。
最后计算出常数与y的系数交叉相乘的差，
即（-5）×2-1×1=-11。
这样x=-11÷11=-1；y=44÷11=4
所以结果为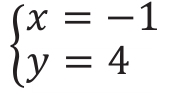
练习
（1）解二元一次方程组
（2）解二元一次方程组
（3）解二元一次方程组
有关印度数学/破解福尔摩斯思维习惯的文章
方法设定200为基准数，计算出两个数与200之间的差。将上两排数字交叉相加所得的结果写在第三排的左边。例子计算186×192=______先计算出186、192与200的差，分别为-14，-8，因此可以写成下列形式：186/-14192/-8交叉相加，186-8或192-14，都等于178。因此可以写成：203/3212/12215/36215×200＋36=43036所以203×212=43036扩展阅读类似的，你还可以用这种方法计算接近250、300、350、400、450、500、550……等数字的乘法，只需选择相应的基准数即可。......
2023-10-27
所谓完全平方数，就是指这个数是某个整数的平方。例如观察这些完全平方数，可以获得对它们的个位数、十位数、数字和等的规律性的认识。性质3：如果完全平方数的十位数字是奇数，则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数。记住完全平方数的这些性质有利于我们判断一个数是不是完全平方数。形如3n＋2型的整数一定不是完全平方数。......
2023-10-27
第一行第一列的位置写上“＋”，然后在下面的格子里竖着写出第一个加数。例子计算457＋214=______将214写在第一列加号的下面，457写在第一行第三四五列。然后对应位置的数字相加：1＋3=4，4＋7=11，2＋2=4，1＋8=9分别写在对应的位置上。所以358＋14=372注意前面空一位是为进位考虑，在最高位相加大于10时向前进位。练习计算126＋671=______计算987＋126=______计算1265＋529=______计算465＋2365=______计算3502＋6545=______计算1328＋7262=______......
2023-10-27
补数是一个数为了成为某个标准数而需要加的数。下面，我们来看一下如何用补数来计算加法吧！做加法一般用的是与其相加能进到下一位的补数，而另外一种补数，也就是与其相加能够得到该位上最大数的补数，以后我们会学习到。......
2023-10-27
相对来说，完全立方数的立方根要比完全平方数的平方根计算起来简单得多。记住这些规律对我们求解一个完全立方数的立方根是有好处的。看最左边一组，看它最接近哪个数的立方，从而确定立方根的第一位数。这个方法对于位数不多的求立方根的完全立方数比较适用。所以9161的立方根为21。所以778688的立方根为92。计算17576的立方根17，57626先看后三位数，尾数为6，所以立方根的尾数为6。所以17576的立方根为26。......
2023-10-27
方法以10的整数倍为基准数，计算出要求的数与基准数的差。将第二步的结果乘以基准数的平方。计算出差的立方。将3、4、5步的结果相加，即可。例子计算133=______基准数为1013-10=313＋3×2=1919×102=1900×3×10=27033=27结果为1900＋270＋27=2197所以133=2197计算623=______基准数为6062-60=262＋2×2=6666×602=237600×2×60=72023=8结果为237600＋720＋8=238328所以623=238328计算373=______基准数为4037-40=-337＋（-3）×2=3131×402=49600×（-3）×40=1080（-3）3=-27结果为49600＋1080-27=50653所以373=50653练习计算213=______计算143=______计算563=______计算773=______计算953=______计算333=______......
2023-10-27
如果两个加数都是三位数，那么我们可以把它们分别分解成百位、十位和个位三部分，然后分别进行计算，最后相加。把两个加数的个位数字相加。把前三步的结果相加，注意进位。例子计算328＋321=______首先计算300＋300=600再计算20＋20=40再计算8＋1=9结果就是600＋40＋9=649所以328＋321=649计算175＋242=______100＋200=30070＋40=1105＋2=7300＋110＋7=417所以175＋242=417计算538＋289=______500＋200=70030＋80=1108＋9=17700＋110＋17=827所以538＋289=827注意这种方法还可以做多位数加多位数，并不一定需要两个加数的位数相等哦。......
2023-10-27
我们做减法的时候，也跟加法一样，一般都是从右往左计算，这样方便借位。而在印度，他们都是从左往右算的。方法我们以减数为三位数为例。先用被减数减去减数的整百数。例子计算458-214=______首先计算458-200=258其次计算258-10=248再计算248-4=244所以458-214=244计算88-21=______首先计算88-20=68再计算68-1=67所以88-21=67计算9125-1186=______9125-1000=81258125-100=80258025-80=79457945-6=7939所以9125-1186=7939注意这种方法其实就是把减数分解成容易计算的数进行计算。练习计算58-21=______计算848-164=______计算856-245=______计算2648-214=______计算5128-1154=______计算43958-12614=______......
2023-10-27
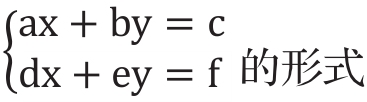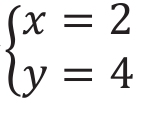
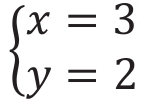
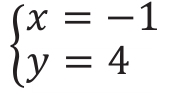
相关推荐