1.单项选择题(1)D (2)B (3)B (4)D (5)C (6)D (7)A (8)B (9)D (10)C (11)B (12)A (13)C (14)B (15)C (16)B (17)A (18)D (19)B (20)D (21)B (22)D (23)D2.解答题(1)(2)(3)(4)(5)(6)(7)由得(8)由于所以(9)由于所以,x→0时,α(x)是x的三阶无穷小.(10)......
2023-10-27
一、单项选择题
(1)D (2)A (3)C (4)B (5)D (6)C
(7)A (8)C (9)C (10)C (11)C (12)C
(13)B
2.解答题
(1)ES2=DX=EX2-(EX)2,(1)
其中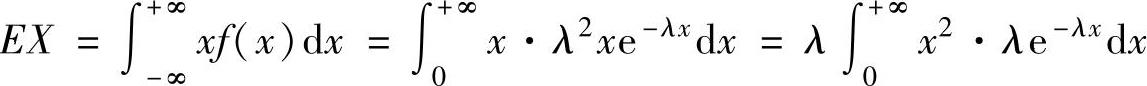 =λET2(其中T~E(λ))
=λET2(其中T~E(λ))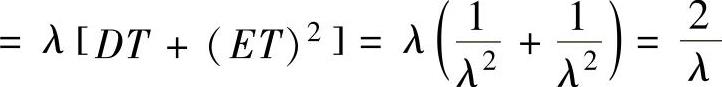 ,(2)
,(2)
将式(2)、式(3)代入式(1)得
(2)由于
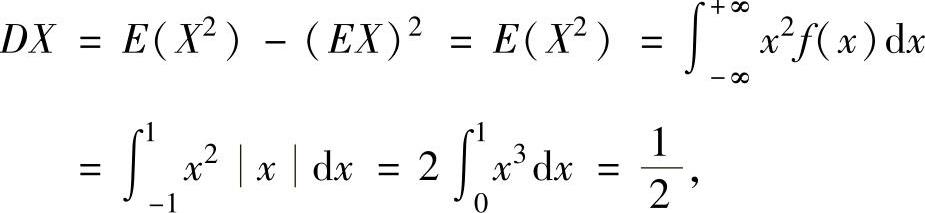
所以,由独立同分布中心极限定理得
(3)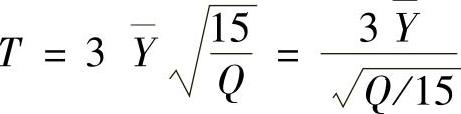 ,其中由
,其中由 知
知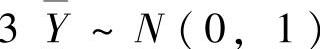 ,此外由
,此外由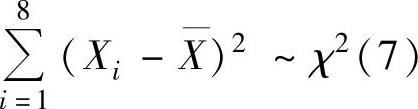 ,
, ,且
,且 与
与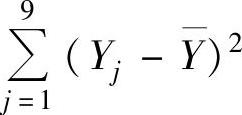 相互独立知
相互独立知
并且3Y与Q相互独立.因此由t分布的定义知T~t(15).
(4)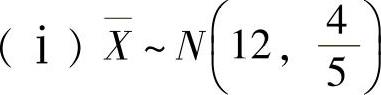 ,所以
,所以
(ⅱ)P(max{X1,X2,…,X5}>15)=1-P(max{X1,X2,…,X5}≤15)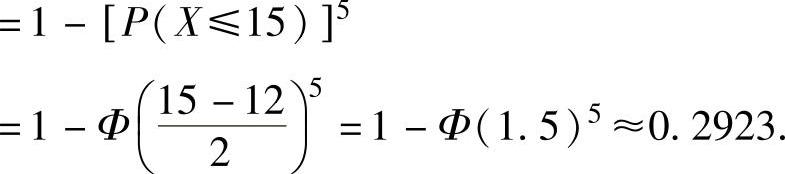
(5)(ⅰ)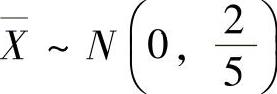 ,
,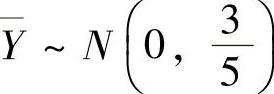 ,并且它们相互独立,所以Z=X-Y~N(0,1).
,并且它们相互独立,所以Z=X-Y~N(0,1).
(ⅱ)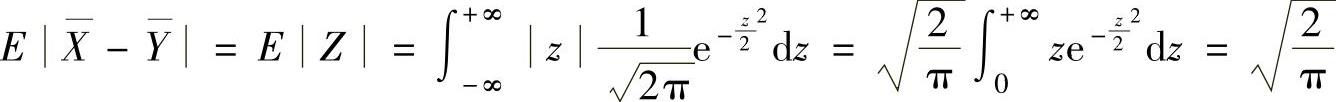 ,
,
(6)由X与S2相互独立知X2与S4相互独立,所以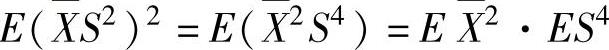 ,(1)其中,
,(1)其中,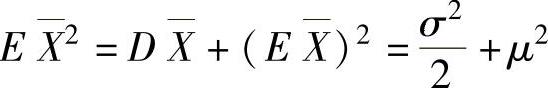 ,(2)
,(2)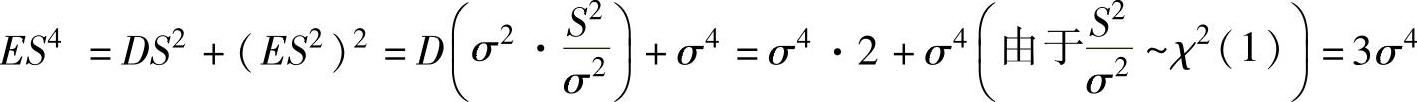 ,(3)
,(3)
将式(2)、式(3)代入式(1)得
(7)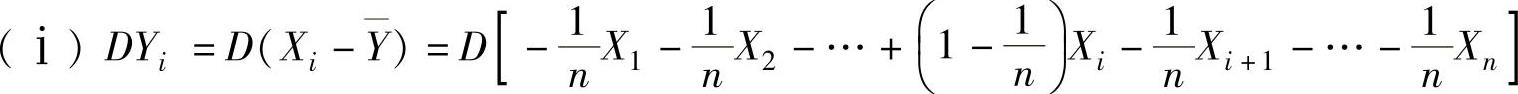

(8)X的分布律为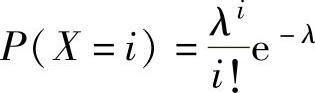 .于是似然函数为(www.chuimin.cn)
.于是似然函数为(www.chuimin.cn)
即 lnL(λ)=K+84lnλ-42λ(其中K=-ln[(2!)12·(3!)8·(4!)4·(5!)2]).
令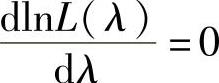 得λ的最大似然估计值λ^ =2.
得λ的最大似然估计值λ^ =2.
(9)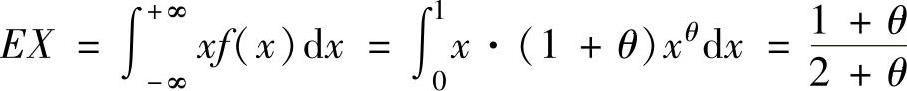 ,记样本均值为X.
,记样本均值为X.
令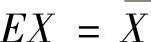 ,即
,即 ,所以θ的矩估计量为
,所以θ的矩估计量为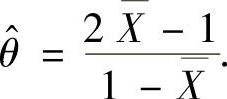
设样本观察值为x1,x2,…,xn,则似然函数为
L(θ)=(1+θ)x1θ·(1+θ)x2θ·…·(1+θ)xnθ
=(1+θ)n(x1x2…xn)θ,
lnL(θ)=nln(1+θ)+θln(x1x2…xn),
令 得
得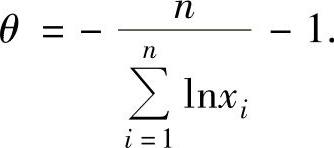 所以θ的最大似然估计量为
所以θ的最大似然估计量为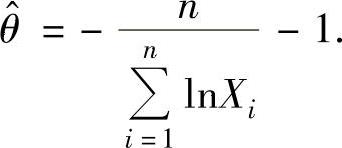
(10)(ⅰ)X的分布函数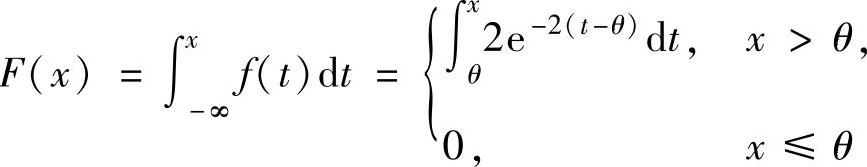
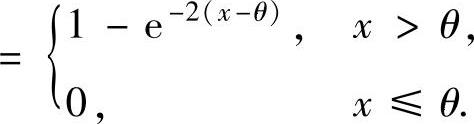
(ⅱ)θ^的分布函数
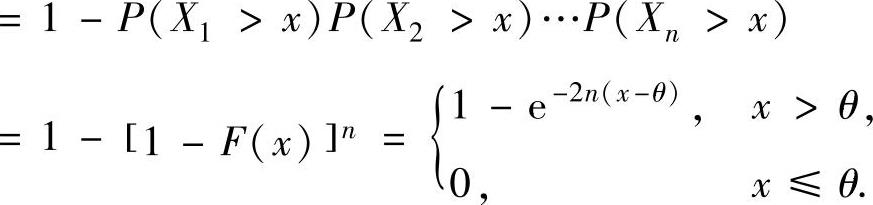
(ⅲ)由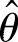 的概率密度
的概率密度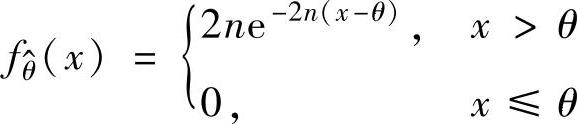 ,知
,知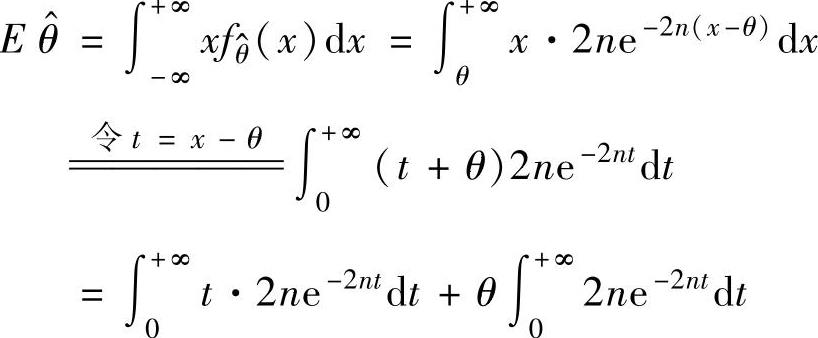
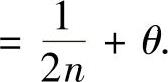
(11)(ⅰ)设样本观察值为x1,x2,…,xn,则似然函数
令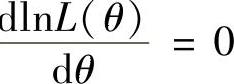 得
得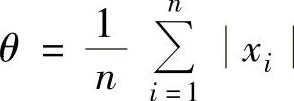 .从而θ的最大似然估计量为
.从而θ的最大似然估计量为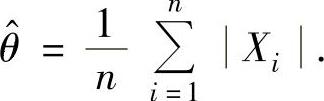
(ⅱ)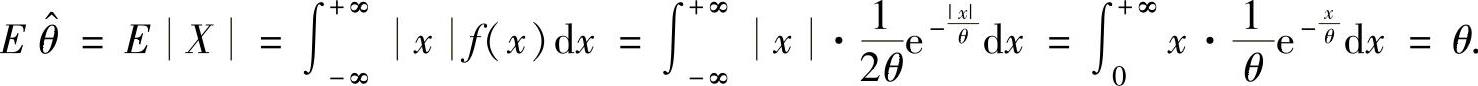
(ⅲ)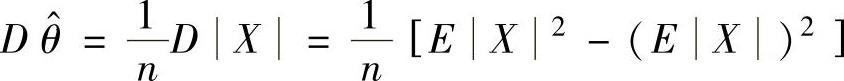
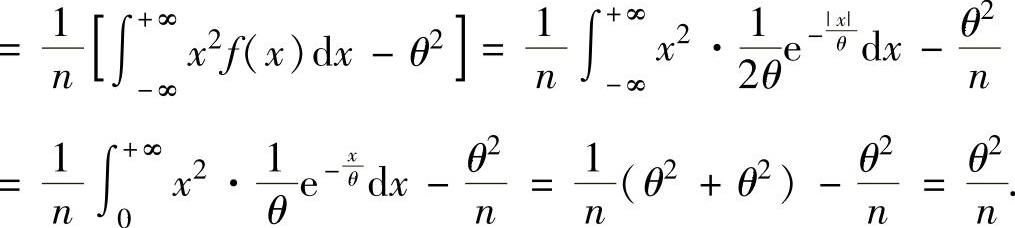
(12)θ的最大似然估计量为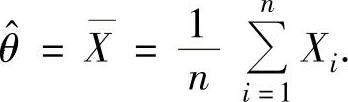 由于对任意实数x有P
由于对任意实数x有P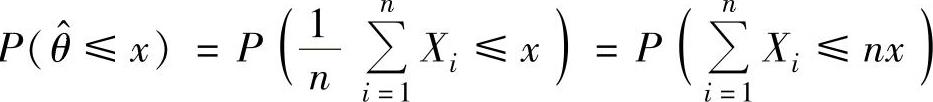 ,其中X1,X2,…,
,其中X1,X2,…,
Xn独立同分布,且数学期望为θ,方差为θ2,所以由独立同分布中心极限定理知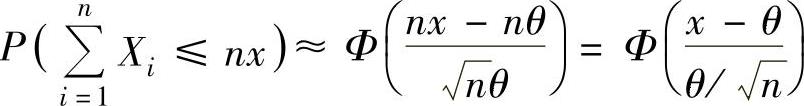 (Φ(x)是N(0,1)的分布函数).
(Φ(x)是N(0,1)的分布函数).
由此得到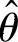 近似服从
近似服从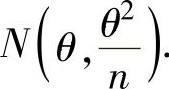
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

1.单项选择题(1)D (2)B (3)B (4)D (5)C (6)D (7)A (8)B (9)D (10)C (11)B (12)A (13)C (14)B (15)C (16)B (17)A (18)D (19)B (20)D (21)B (22)D (23)D2.解答题(1)(2)(3)(4)(5)(6)(7)由得(8)由于所以(9)由于所以,x→0时,α(x)是x的三阶无穷小.(10)......
2023-10-27

1.单项选择题(1)A (2)C (3)D (4)B (5)C(6)C (7)D (8)C (9)D (10)D(11)A (12)A (13)C (14)B2.解答题(1)φ′(x)=f1′·2x+f2′(f1′·2x+f2′),φ′(1)=2×2+3(2×2+3)=25.(2)对所给方程两边求全微分dz-dx-dy+yez-xdx+xez-xdy+xyez-x(dz-dx)=0,即(1+xye......
2023-10-27

【主要内容】服从二维正态分布的随机变量有以下常用的性质:(1)设(X,Y)~N(μ1,μ2,σ21,σ22,ρ),则X~N(μ1,σ21),Y~N(μ2,σ22);反之,如果X与Y相互独立,且X~N(μ1,σ21),Y~N(μ2,σ22),则(X,Y)~N(μ1,μ2,σ21,σ22,0)(注意:这个结论中X与Y相互独立的条件是不可缺少的).(2)设(X,Y)~N(μ1,μ2,σ21,σ22,ρ)......
2023-10-27

),且取这些值对应的概率为pij(i=1,2,…),p·j=Σipij(j=1,2,…).4.二维离散型随机变量的条件分布律设(X,Y)是二维离散型随机变量,它的分布律及边缘分布律分别为P=pij(i=1,2,…......
2023-10-27

,n)为n元二次型.记aji=aij(i,j=1,2,…,xn)=xTAx.2.二次型化标准形的方法如果二次型中只含有变量的平方项,则称这种二次型为标准形.设二次型f(x1,x2,…,xn)T),则它有以下两种化标准形的方法:可逆线性变换法由于对实对称矩阵A,存在可逆矩阵C,使得,所以令x=Cy(可逆线性变换,其中,y=(y1,y2,…,xn)化为标准形d1y21+d2y22+…......
2023-10-27
相关推荐