定位特征是为构造新特征提供定位功能的,它包括工作平面、工作轴、工作点。可以将工作平面作为新的草图平面,也可以将它作为特征的限位面以及装配时的辅助定位面。单击“模型”选项卡中的“定位特征”选项,如图5-37所示,即可以生成工作平面等。图5-36系统默认的定位特征图5-37“定位特征”工具条1.工作平面的创建创建工作平面的方法就是根据几何知识确定平面的方法。......
2025-09-29
【主要内容】
1.参数点估计的概念
设总体X的概率分布形式已知,但含有未知参数θ,对θ的点估计就是借助总体X的简单随机样本X1,X2,…,Xn(观察值为x1,x2,…,xn),用适当的统计量θ^(X1,X2,…,Xn)作为θ的估计量,用θ^(X1,X2,…,Xn)的观察值θ^(x1,x2,…,xn)作为θ的估计值.
2.参数的点估计方法
参数点估计有两种常用方法:
(1)矩估计法
用样本矩作为相应的总体矩(包含待估参数θ)的估计量(或估计值),对θ作出点估计.这种方法称为参数θ的矩估计法.
(2)最大似然估计法
根据总体分布和样本构造似然函数(包含待估参数θ),取使似然函数达到最大值的θ^作为θ的估计量(或估计值).这种方法称为θ的最大似然估计法.
似然函数的作法如下:
设总体X是离散型随机变量,它的分布律P(X=x)=p(x;θ)(θ是待估参数),则此时的似然函数L(x1,x2,…,xn;θ)(或简记为L(θ))为
L(θ)=p(x1;θ)p(x2;θ)…p(xn;θ),其中x1,x2,…,xn是相应于来自总体X的简单随机样本X1,X2,…,Xn的观察值.
设总体X是连续型随机变量,它的概率密度为f(x;θ)(θ是待估参数),则此时的似然函数L(x1,x2,…,xn;θ)(或简记为L(θ))为
L(θ)=f(x1;θ)f(x2;θ)…f(xn;θ),其中x1,x2,…,xn是相应于来自总体X的简单随机样本X1,X2,…,Xn的观察值.
3.常用总体的参数点估计设(X1,X2,…,Xn)是来自总体X的一个简单随机样本,其中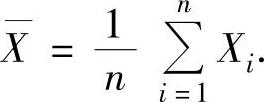
【典型例题】
例8.3.1 设总体X的概率密度为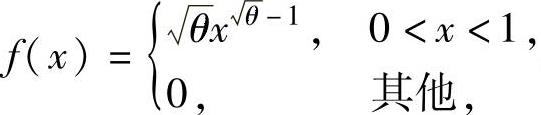 其中θ>0是未知参数,x1,x2,…,xn是来自总体X的一个样本观察值.分别用矩估计法和最大似然估计法计算θ的估计值.
其中θ>0是未知参数,x1,x2,…,xn是来自总体X的一个样本观察值.分别用矩估计法和最大似然估计法计算θ的估计值.
精解 (1)矩估计法.因为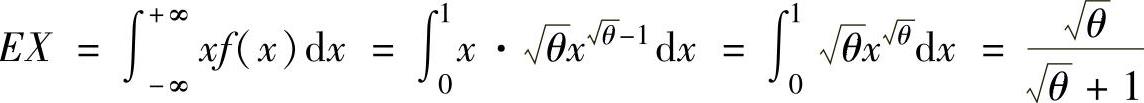 ,所以,由矩估计法得
,所以,由矩估计法得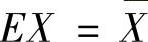 (其中
(其中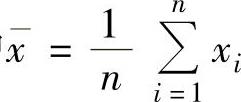 ),即
),即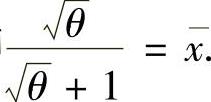 解此方程得
解此方程得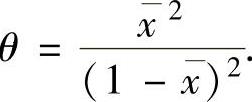 因此由矩估计法所得的
因此由矩估计法所得的
θ的估计值为
(2)最大似然估计法.
似然函数为L(θ)=f(x1)f(x2)…f(xn)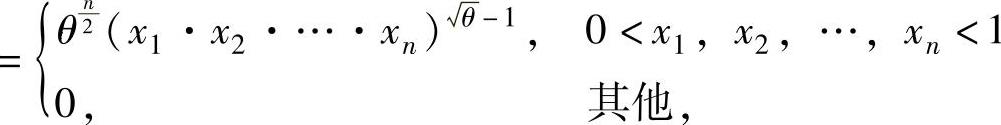 ,
,
显然,L(θ)只能在0<x1,x2,…,xn<1的点(x1,x2,…,xn)处取到最大值,故可取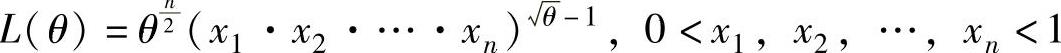 ,
,
即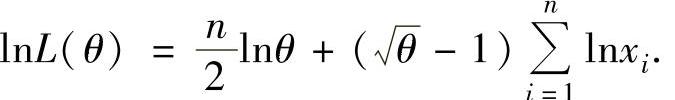
由最大似然估计法,令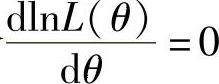 ,即
,即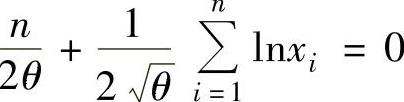 ,
,
此方程的解即为θ的最大似然估计值
例8.3.2 设总体X的分布律为
其中,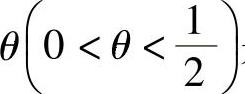 是未知参数.设3,1,3,0,3,1,2,3是X的一个样本观察值,分别
是未知参数.设3,1,3,0,3,1,2,3是X的一个样本观察值,分别
用矩估计法和最大似然估计法计算θ的估计值.
精解 (1)矩估计法.(https://www.chuimin.cn)
因为EX=0·θ2+1·2θ(1-θ)+2·θ2+3·(1-2θ)
=3-4θ,
所以,由矩估计法得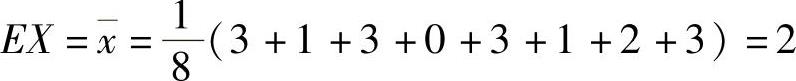 ,即3-4θ=2.
,即3-4θ=2.
解此方程得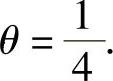 因此由矩估计法得θ的估计值为
因此由矩估计法得θ的估计值为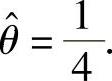
(2)最大似然估计法.
似然函数L(θ)=P(X=0)·[P(X=1)]2·P(X=2)·[P(X=3)]4
=θ2·[2θ(1-θ)]2·θ2·(1-2θ)4=4θ6(1-θ)2(1-2θ)4,即lnL(θ)=ln4+6lnθ+2ln(1-θ)+4ln(1-2θ).
由最大似然估计法,令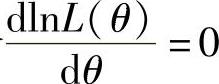 ,即
,即
此方程位于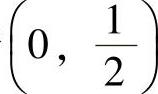 内的解,即为θ的最大似然估计值
内的解,即为θ的最大似然估计值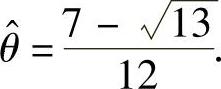
例8.3.3 设X1,X2,…,Xn是来自总体X的简单随机样本,其中X的概率密度为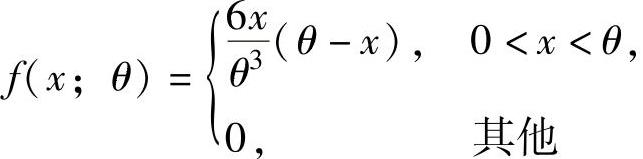 (θ是未知参数).
(θ是未知参数).
求参数θ的矩计量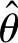 ,并计算D
,并计算D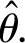
精解 因为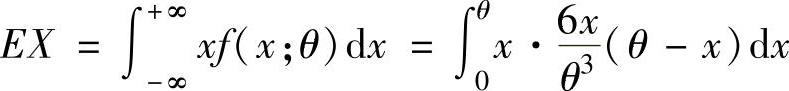
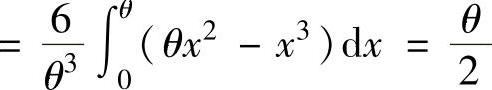 ,
,
所以,由矩估计法得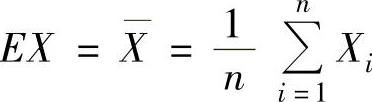 ,即
,即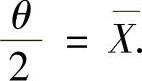 所以θ的矩估计量
所以θ的矩估计量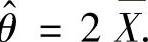
下面计算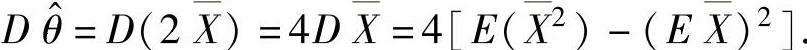
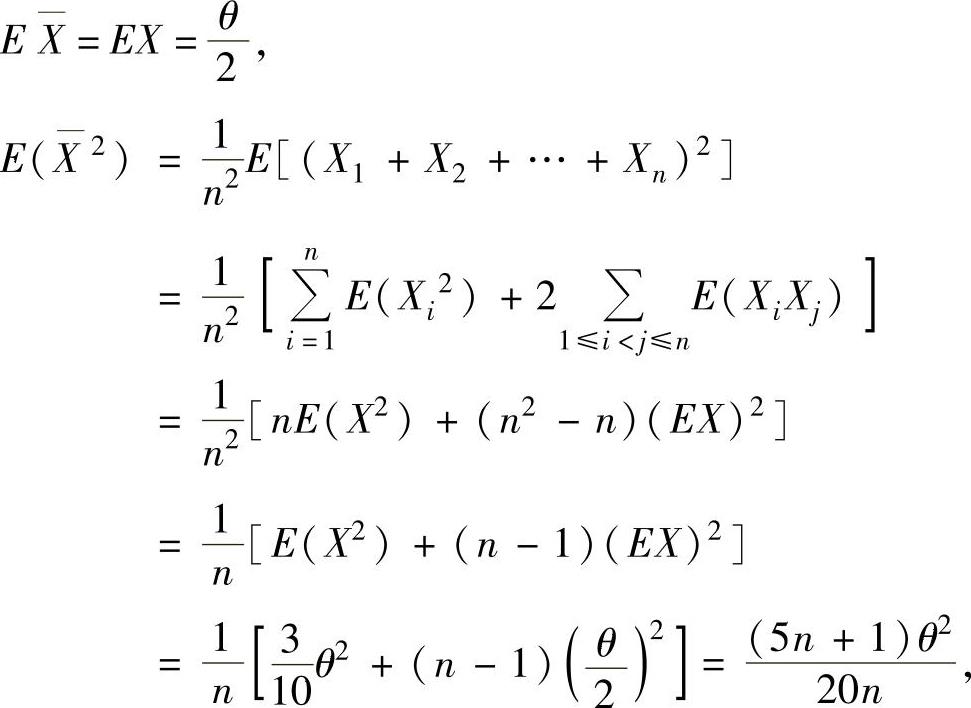 其中
其中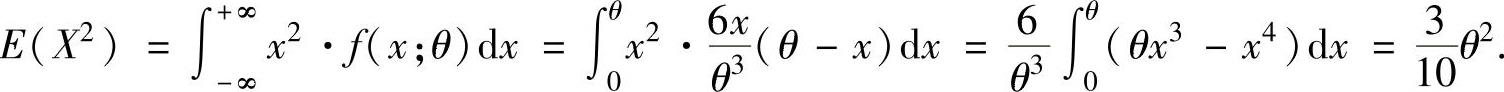 所以,
所以,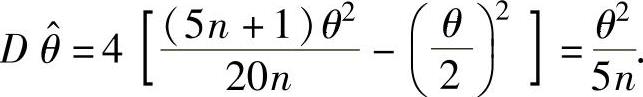
例8.3.4 设某种元件的使用寿命X的概率密度为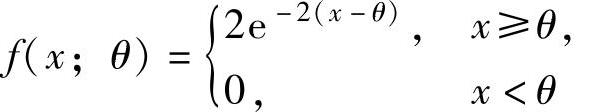 (其中θ是未知参数),
(其中θ是未知参数),
又设X1,X2,…,Xn(n>1)是来自总体X的简单随机样本,求:
(1)θ的矩估计量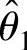 ;
;
(2)θ的最大似然估计量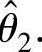
精解 (1)由于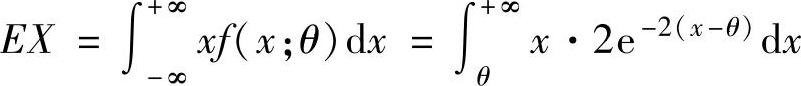
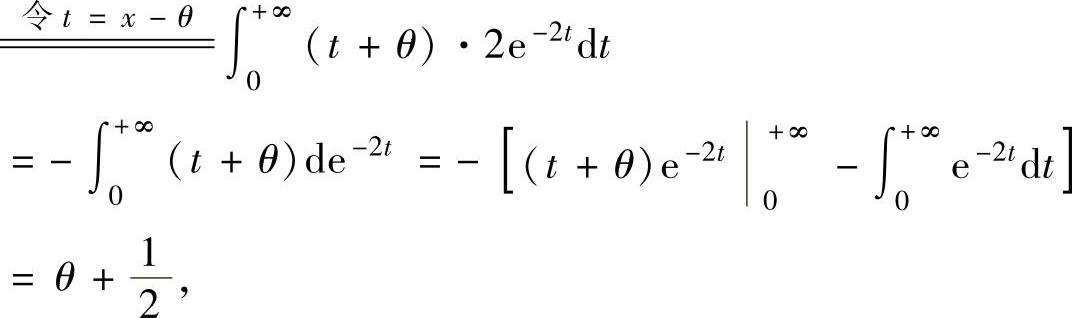
所以,由矩估计法得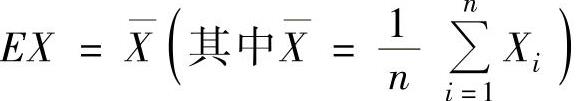 ,即
,即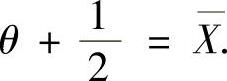 所以θ的矩估计量
所以θ的矩估计量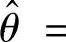
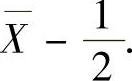
(2)设x1,x2,…,xn是样本X1,X2,…,Xn的观察值,则似然函数为L(θ)=f(x1)f(x2)…f(xn)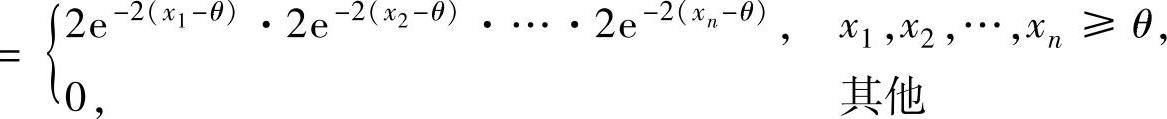

显然,L(θ)的最大值只能在x1,x2,…,xn≥θ处取到,所以可取
由于L(θ)是θ的单调增加函数,所以当θ=min{x1,x2,…,xn}时,L(θ)取最大值.因此由θ的最大似然估计量为
例8.3.5 设总体X~N(μ,σ2),X1,X2,…,Xn是它的一个简单随机样本,求使得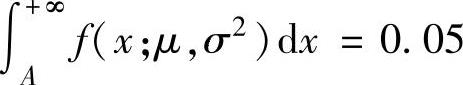 的点A的最大似然估计量,其中f(x;μ,σ2)是X的概率密度,μ,σ2是未知参数.
的点A的最大似然估计量,其中f(x;μ,σ2)是X的概率密度,μ,σ2是未知参数.
精解 将A表示成关于μ,σ2的函数,然后用μ,σ2的最大似然估计量算出A的最大似然估计量.
由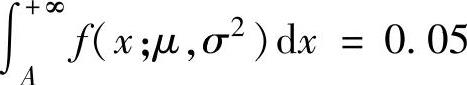 ,即
,即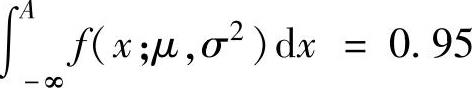 得
得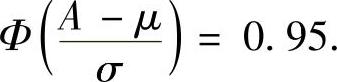 查表得
查表得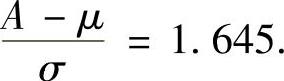 于是A的最大似然估计量为
于是A的最大似然估计量为
其中,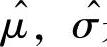 是μ,σ的最大似然估计量,它们分别为
是μ,σ的最大似然估计量,它们分别为
所以,A的最大似然估计量为
相关文章

定位特征是为构造新特征提供定位功能的,它包括工作平面、工作轴、工作点。可以将工作平面作为新的草图平面,也可以将它作为特征的限位面以及装配时的辅助定位面。单击“模型”选项卡中的“定位特征”选项,如图5-37所示,即可以生成工作平面等。图5-36系统默认的定位特征图5-37“定位特征”工具条1.工作平面的创建创建工作平面的方法就是根据几何知识确定平面的方法。......
2025-09-29

从数量众多的艺术美学理论成果,特别是教材编写出版情况来看,学术界对西方传统美学的研究与应用较为普遍、清晰,而对马克思主义美学中国化的理论研究及其应用,显得目标不明、思路不清。可以说,刘纲纪运用中国化的马克思主义美学理论研究并阐述中国艺术美学理论,在谢赫画论研究上达到了较为圆熟的境界,是马克思主义美学中国化及其在艺术美学领域成熟应用的杰出范例。......
2025-09-30

塑料除了增强改性之外,还广泛采用了共混、填充等改性方法。总之,可根据塑料成品的使用工艺性要求,有针对地加入某些填料,既可以改善其性能,又可以降低塑料的成本。这实质上也是对塑料的一种改性。例如,ABS塑料综合了丙烯腈、丁二烯和苯乙烯三种组成物的性能。用于电镀的聚酰胺是以矿物为填料进行填充改性的,它具有优异的强度、刚度、耐热性和尺寸稳定性。它与其他改性聚苯醚方法相比,在相同质量下,刚度高得多。......
2025-09-29

观测人体运动要确定观测对象及观测坐标系。在人体运动的研究中,最常用的是直角坐标系。常用的直角坐标系有三种:一维坐标系:直线运动,沿着一个方向运动,如一百米跑、游泳等。视频跟踪法是应用视频对人体的运动进行跟踪、捕捉和分析。图3-18摄影观察法人体运动属于非刚体运动的范畴,具有高度的非线性特点。......
2025-09-29

差距模式是当前学习障碍儿童鉴别和评估的主要方法,可操作性强。差距法也称常模参照法、标准化测验法,这是因为差距模式的评估首先需要标准化的智力测验和标准化的成就测验。该差距模式源于学习障碍定义中所强调的潜能与实际表现之间的差距。差距模式使用差距分数作为筛查的指标。差距分数的衡量方法主要有年级水平差距法、成就水平期望公式法、标准分数差距法和回归分析法四种。......
2025-09-29

采用燃油、燃气火焰炉加热时,与工件接触的主要介质是燃料燃烧的产物——燃烧气体,其主要成分是CO2、N2、CO及H2等。这些加热介质中存在的氧化、脱碳等有害气体将会对工件表面造成破坏。因此,气体加热介质已发展到可以控制炉气成分以实现光亮加热或无氧化加热的阶段。表7-1可控气氛的组成及用途此外,还可采用氮、氩气等保护气氛作为加热介质。......
2025-09-29

,n)的价值评定量,相应的关联矩阵表见表9-7。表9-7 关联矩阵表应用关联矩阵评价方法的关键,在于确定各评价指标的相对重要度,即权重ωi以及由评价主体给定的评价指标的评价尺度。在表9-11中,外观的重要性是实施费用的0.5倍,经济损失减少的重要性是外观的2倍,负伤者减少的重要性又是经济损失的3倍,死亡者减少的重要性是负伤者减少的3倍。......
2025-09-29

在此假设基础上,可用EMD对任何信号进行分解。ICA由观测信号及对源信号的概率分布的估计来确定源,可有效避免因提高信噪比而产生的缺陷等。ICA可在语音信号分离、生物医学信号处理、金融数据分析、图像消噪、远程通信、人脸识别等方面有重要应用价值。2)遗传算法的新结构、基因操作策略及性能。3)遗传算法参数的选择及与其他算法的综合。......
2025-09-29
相关推荐