,Xn是来自总体X的容量为n的简单随机样本,简称样本,它的观察值x1,x2,…,Y9分别是来自相互独立总体X~N和Y~N的简单随机样本,求统计量所服从的分布.精解 由于X1,X2,…......
2023-10-27
【主要内容】
1.一个正态总体情形
设总体X~N(μ,σ2)(此时简称X是正态总体),X1,X2,…,Xn是来自X的一个简单随机样本,其均值为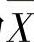 ,方差为S2,则有关统计量及其分布如下:
,方差为S2,则有关统计量及其分布如下:
(1)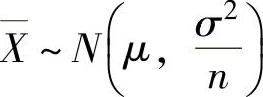 ,即
,即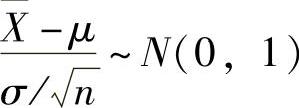 ,并且
,并且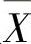 与S2相互独立.
与S2相互独立.
(2)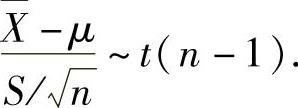
(3)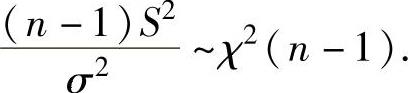
2.两个正态总体情形
设总体X~N(μ1,σ12),Y~N(μ2,σ22),它们相互独立.X1,X2,…,Xn1和Y1,Y2,…,Yn2分别是来自总体X和Y的简单随机样本,它们的均值分别为X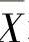 和
和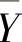 ,方差分别为S12和S22,则有关统计量及其分布如下:
,方差分别为S12和S22,则有关统计量及其分布如下:
(1)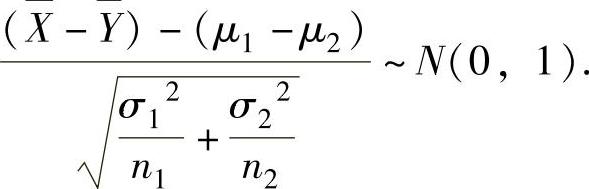
(2)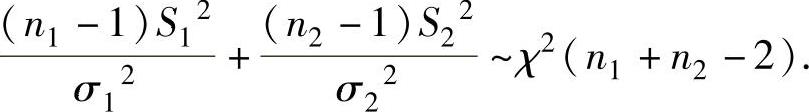
(3)当σ1=σ2时,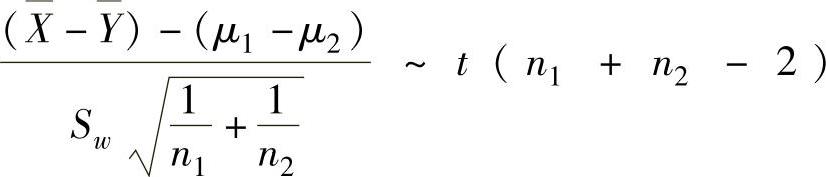 ,其中Sw2=
,其中Sw2=
【典型例题】
例8.2.1 (单项选择题)设X1,X2,…,X9是来自总体X~N(μ,σ2)的简单随机样本.记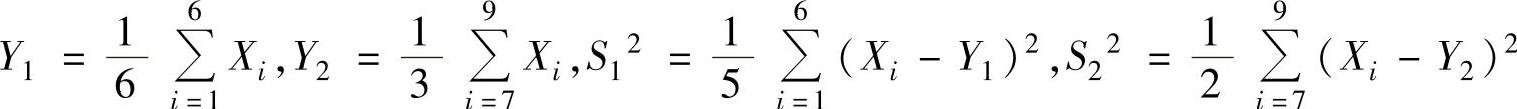 ,则随机变量
,则随机变量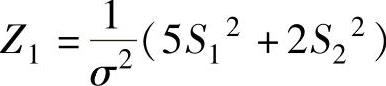 ,
,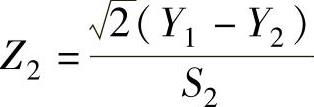 分别服从( ).A.χ2(9),t(2)B.χ2(7),t(3)C.χ2(7),t(2)D.χ2(9),t(3)
分别服从( ).A.χ2(9),t(2)B.χ2(7),t(3)C.χ2(7),t(2)D.χ2(9),t(3)
精解 先考虑Z1.
由于随机变量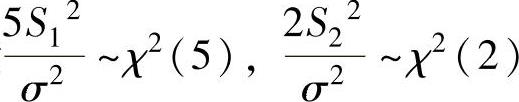 ,且它们相互独立,所以由χ2分布的性质得
,且它们相互独立,所以由χ2分布的性质得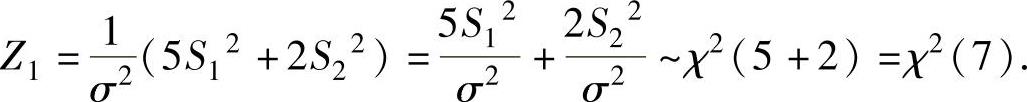
下面考虑Z2.
由随机变量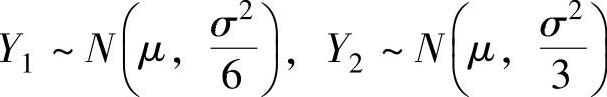 ,且它们相互独立知
,且它们相互独立知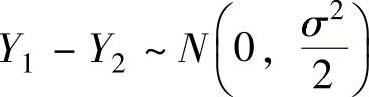 ,
,
所以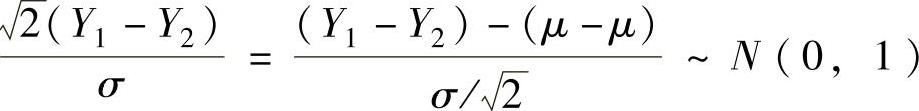 .由上已知
.由上已知 此外,
此外,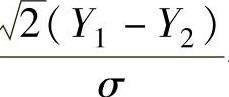 与
与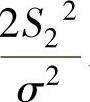 相互独立(这是由于Y1与S22相互独立,Y2与S22相互独立,所以
相互独立(这是由于Y1与S22相互独立,Y2与S22相互独立,所以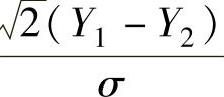 与
与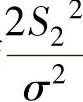 相互独立),所以由t分布的定义得
相互独立),所以由t分布的定义得
因此本题选C.
例8.2.2 设X1,X2,X3,X4是来自正态总体X~N(0,22)的简单随机样本.记Z=a(X1-2X2)2+b(3X3-4X4)2,求参数a,b(a>0,b>0)的值,使得Z服从χ2分布,并求这个χ2分布的自由度.(www.chuimin.cn)
精解 记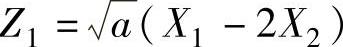 ,
,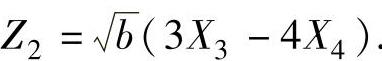 要使Z服从χ2分布,必须使Z1,
要使Z服从χ2分布,必须使Z1,
Z2~N(0,1),从而a,b应满足 即
即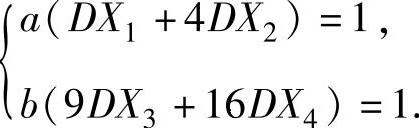
由此得到a(4+4×4)=1,即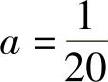 ;b(9×4+16×4)=1,即
;b(9×4+16×4)=1,即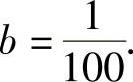
此时,Z=Z12+Z22,其中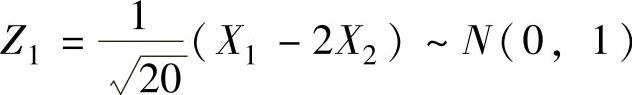 ,
,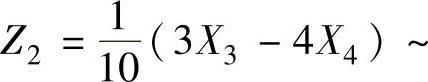 N(0,1),且Z1与Z2相互独立,所以Z服从自由度为2的χ2分布.
N(0,1),且Z1与Z2相互独立,所以Z服从自由度为2的χ2分布.
例8.2.3 设X1,X2是来自总体X~N(0,1)的一个简单随机样本.
(1)证明:随机变量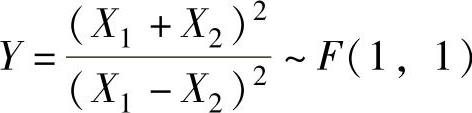 ,并求概率P(Y≤39.86);
,并求概率P(Y≤39.86);
(2)已知概率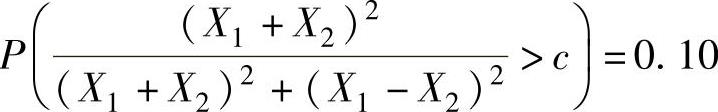 ,求常数c.
,求常数c.
精解 (1)记Y1=X1+X2,Y2=X1-X2,则Y1,Y2都服从N(0,2),所以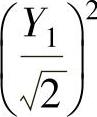 和
和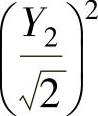 都服从χ2(1).
都服从χ2(1).
此外,由Cov(Y1,Y2)=Cov(X1+X2,X1-X2)=Cov(X1,X1)-Cov(X2,X2)=DX1-DX2=1-1=0
知Y1与Y2相互独立,即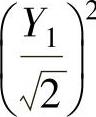 与
与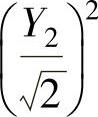 相互独立.于是由F分布的定义得证
相互独立.于是由F分布的定义得证
查表
由此可得P(Y≤39.86)=1-P(Y>39.86)1-0.10=0.90.
(2)由于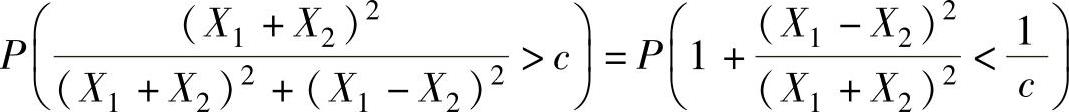
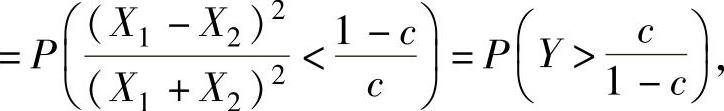
所以由题设得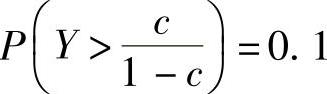 ,查F(1,1)分布表得
,查F(1,1)分布表得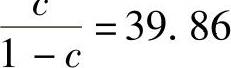 ,所以c=0.97.
,所以c=0.97.
例8.2.4 设总体X~N(μ1,σ2),Y~N(μ2,σ2),它们相互独立.又设X1,X2,…,Xn1和Y1,Y2,…,Yn2分别是来自X和Y的简单随机样本,记
求EZ和DZ.
精解 由两个正态情形的样本统计量的分布知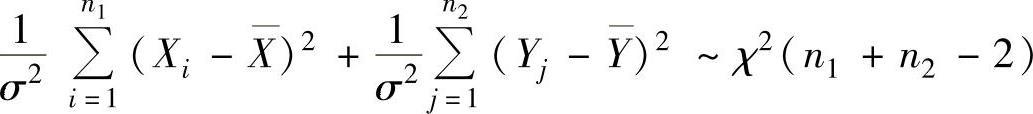 ,
,
所以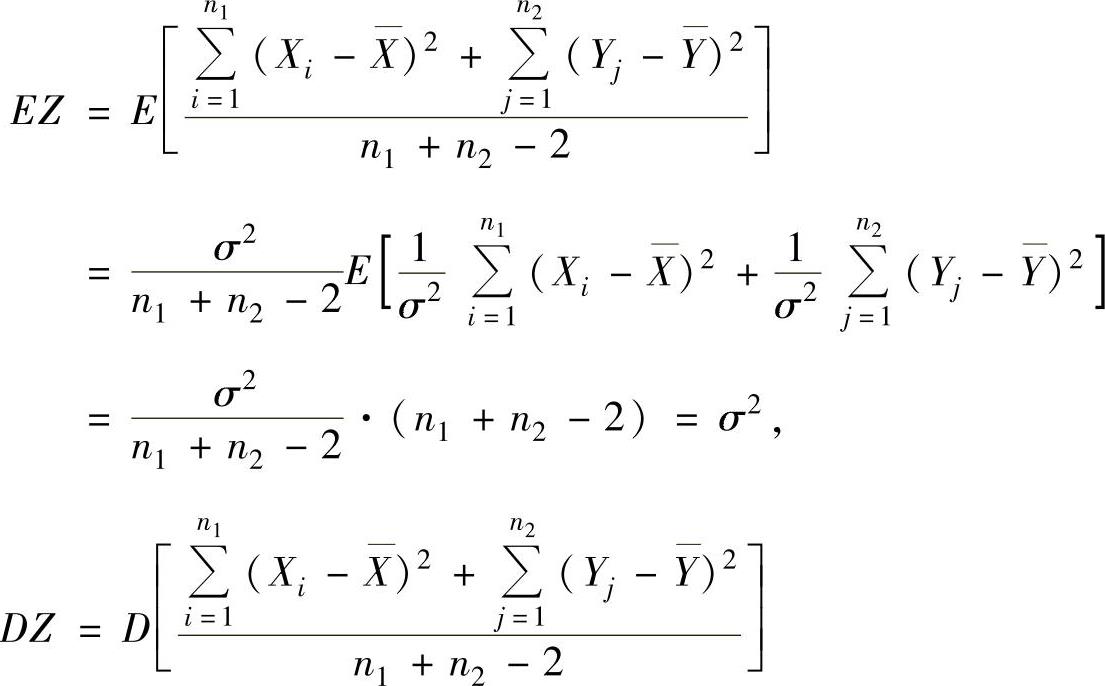
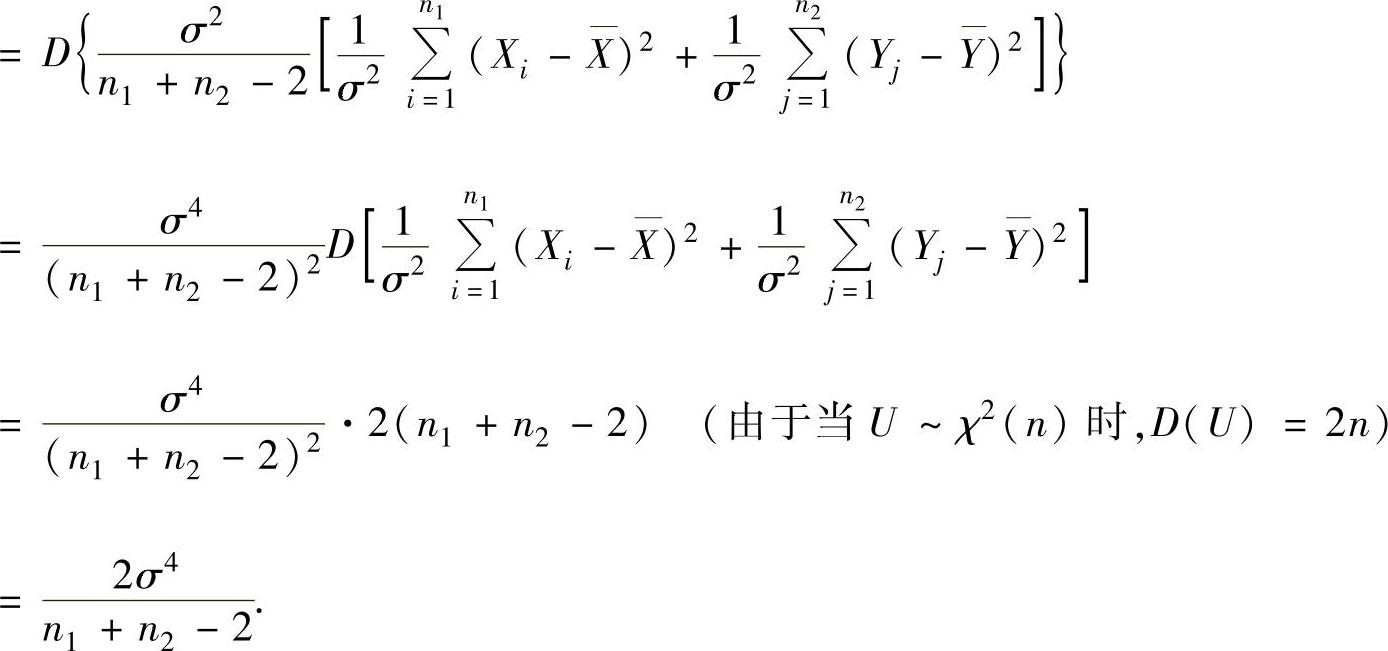
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

,Xn是来自总体X的容量为n的简单随机样本,简称样本,它的观察值x1,x2,…,Y9分别是来自相互独立总体X~N和Y~N的简单随机样本,求统计量所服从的分布.精解 由于X1,X2,…......
2023-10-27

PISA采用按照概率与抽样元素的规模大小成比例的抽样法,是以上海所有的在7年级及以上就读的15岁学生作为调查总体,首先采用与学生规模等概率抽样的方法抽取学校样本,然后在每所样本学校随机抽取同样数量的学生。第二阶段是学生抽样,由SHPISA研究中心根据PISA协作组织反馈的样本学校名单,收集这些学校所有15岁学生的名单,与前期各学校提交的学生数据核对。中国上海共计抽取了符合PISA参加资格的学生6 467名。......
2023-10-19

桥梁总体布置图包括桥梁平面图、立面图和横断面图。桥梁的线形及桥头引道的平面布置原则以能使车辆平稳舒适地通过为宜。图1.2.11桥梁总体布置图2. 桥梁立面图桥梁立面图主要表明桥梁的类型、跨度、桥下净空高度、桥梁的分孔、桥墩与桥台的形式、桥梁总体尺寸、各种主要构件的相互位置关系、各部分的高程、桥上和桥头引道的纵坡以及基础的埋置深度等情况,为施工时确定墩台位置、安装构件和控制标高的依据。......
2023-06-23

样本平均数的分布与其他分布一样,有两个重要参数,一个是样本平均数的平均数,记作μ,另一个是样本平均数的方差,记作。标准误大,各样本平均数间差异程度大,样本平均数的精确性低。从某特定总体抽样,因为σ是一定值,所以只有增大样本容量,才能降低样本平均数的抽样误差。......
2023-11-17

迤东、迤西、迤南地区各城镇、矿厂、村寨的会馆均在乾嘉间建立。这一期间,云南各地新建会馆54所,新建会馆总数仅次于乾隆时期。昭通府、开化府、广南府的乡村地区,是移民会馆分布密集,会馆分布与乡村村落的形成相吻合。云南府虽然商业发达,但是境内矿厂较少,会馆地理分布较其他地区稀疏。云南府、迤西、迤东、迤南四个区域的14个府、4个直隶厅、2个直隶州会馆分布呈现不均衡性特征。......
2023-10-30

(一)大一统思想大一统,即推崇一统于天子的政治思想,它符合战国以来历史发展的趋势和广大人民的根本利益,特别是符合汉武帝时代的政治统一、国家统一和民族融合的历史现实。汉武帝时代是中国历史上空前的统一时代,汉武帝把儒家的大一统思想作为处理国家事务的指导思想,并以此来建构中央集权制度的统治体系,这是一种历史的进步。......
2023-11-28
相关推荐