如前所述，大数定律揭示了大量随机变量的平均结果的稳定性，但没有涉及随机变量的分布。而中心极限定理则进一步揭示出大量相互独立的随机变量之和近似服从正态分布的一般规律，可以用于计算任一随机结果发生的具体概率。中心极限定理以严格的数学形式阐明了在大样本条件下，不论总体的分布如何，样本的均值总是近似地服从正态分布。这使得正态分布在数理统计中具有很重要的地位，并得到了广泛应用。......
2023-08-11
大数定律与中心极限定理20
【摘要】：是相互独立且服从同一分布的随机变量序列，其数学期望都为μ，则对任意ε>0有，即伯努利大数定律设在每次试验中事件A发生的概率为P=p，在n次独立重复试验中，A发生的次数为nA，则对任意ε>0有，即2.中心极限定理列维-林德伯格定理设X1，X2，…，当n充分大时，对任意实数a，b（a
【主要内容】
1.大数定律
（1）切比雪夫大数定律
设X1，X2，…，Xn，…是相互独立的随机变量序列，具有相同的数学期望μ和方差σ2，则对任意ε>0有
记
，则上式成为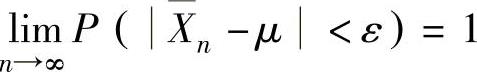
，称为随机变量序列X1，
，…，
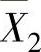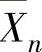，…依概率收敛于μ，记为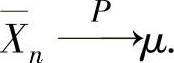
（2）辛钦大数定律
设X1，X2，…，Xn，…是相互独立且服从同一分布的随机变量序列，其数学期望都为μ，则对任意ε>0有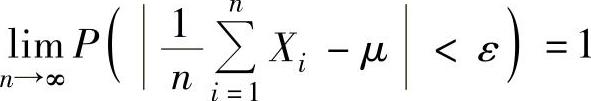
，
即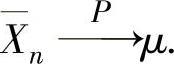
（3）伯努利大数定律
设在每次试验中事件A发生的概率为P（A）=p（0<p<1），在n次独立重复试验中，A发生的次数为nA，则对任意ε>0有
，
即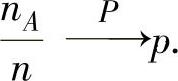
2.中心极限定理
（1）列维-林德伯格定理（独立同分布中心极限定理）
设X1，X2，…，Xn，…是相互独立同分布的随机变量序列，具有相同的数学期望μ和方差σ2，则对任意实数x有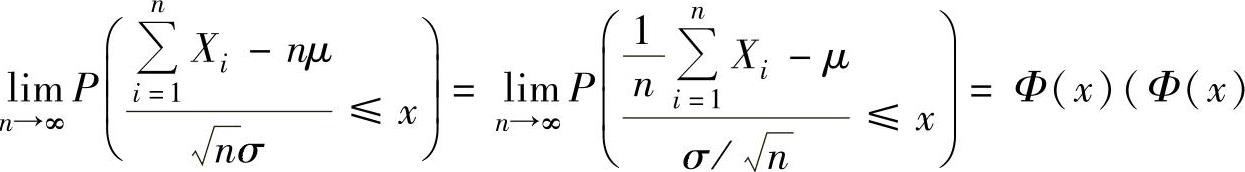
是标准正态分布函数）.
注 由上述定理可知，对于具有相同数学期望μ和方差σ2的独立同分布随机变量序列X1，X2，…，Xn，…，当n充分大时，对任意实数a，b（a<b），有
（2）棣莫弗-拉普拉斯中心极限定理
设随机变量序列X1，X2，…，Xn，…，其中Xn～B（n，p）（n=1，2，…），则对任意实数x有
注 由上述定理可知，对随机变量序列X1，X2，…，Xn，…，其中Xn～B（n，p）（n=1，2，…），当n充分大时，对任意实数a，b（a<b）有
【典型例题】
例7.20.1 设X1，X2，…，Xn，…是独立同分布的随机变量序列，它们服从参数为2的指数分布，则随机变量序列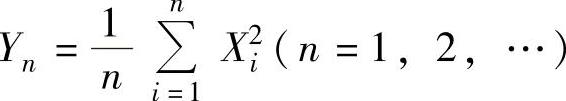
依概率收敛于常数c，求c的值.
精解 由X1，X2，…，Xn，…独立同分布知X21，X22，…，X2n，…也独立同分布，且有相同的数学期望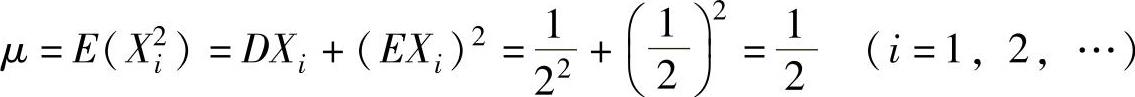
，
所以由辛钦大数定律知
于是，所求的常数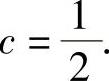
例7.20.2 （单项选择题）设随机变量序列X1，X2，…，Xn，…相互独立且同服从参数为λ（λ>0）的指数分布，则下列结论中正确的是（）.
其中，Φ（x）是标准正态分布函数.
精解 可用中心极限定理直接判定正确的选项.(www.chuimin.cn)
由于X1，X2，…，Xn，…独立同分布，则对于i=1，2，…有
所以由列维-林德伯格中心极限定理得
即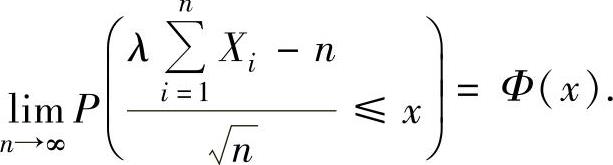
因此本题选A.
例7.20.3 计算机进行加法计算时，把每个加数取为最接近于它的整数来计算.设所有取整误差是相互独立的随机变量，且都服从[-0.5，0.5]上的均匀分布，求300个数相加时误差总和的绝对值小于10的概率.
精解 记Xi是第i个加数的取整误差，则μ=EXi=0，
（i=1，2，…，
300）.所以所求的概率
例7.20.4 一生产线生产的产品成箱包装，每箱的重量是随机变量.假设每箱平均重50kg，标准差5kg.若用最大载重量为5t的汽车来运，求每辆车最多可以装多少箱，才能保证不超载的概率大于0.977（注：（标准差）2=方差）.
精解 设每辆车最多可以装n箱，而每箱的重量是随机变量，记为Xi（i=1，2，…，n）.虽然不知道Xi服从什么分布，但它们独立同分布，且EXi=50，DXi=52=25（i=1，2，…，n）.于是，由列维-林德伯格中心极限定理知，
查表得 Φ（2）=0.977，所以式（1）成为
由于Φ（x）是单调增加函数，所以有
解此不等式得n<98.0199.由此可知，每辆车最多装98箱，才可以保证不超载的概率大于0.977.
例7.20.5 随机地选取两组学生，每组80人，分别在两个实验室里测量某种化合物的pH值.各组测量结果是随机变量，它们相互独立同分布，其数学期望与方差分别为5和0.3，以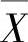
，
分别表示第一组和第二组所得结果的算术平均值.求概率P（4.9<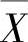
<5.1）和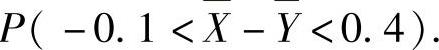
精解 设第一组学生测量结果为Xi（i=1，2，…，80），第二组学生测量结果为Yi（i=1，2，…，80），则由题设知
μ=EXi=EYi=5，DXi=DYi=0.3（i=1，2，…，80）.所以，由列维-林德伯格中心极限定理知
容易知道，μ1=E（Xi-Yi）=EXi-EYi=5-5=0，
σ21=D（Xi-Yi）=DXi+DYi=0.3+0.3=0.6（i=1，2，…，80），
所以，由列维-林德伯格中心极限定理得
例7.20.6 一食品店有三种蛋糕出售，由于售出哪一种蛋糕是随机的，因而售出一块蛋糕的价格是一个随机变量，它取1（元），1.2（元），1.5（元）各个值的概率分别为0.3，0.2，0.5.已知某天售出300块蛋糕，求：
（1）这天收入多于400（元）的概率；
（2）这天售出价格为1.2（元）的蛋糕多于60块的概率.
精解 （1）记Xi是售出的第i块蛋糕的价格，i=1，2，…，300，则X1，X2，…，X300独立同分布，i=1，2，…，300，Xi的分布律为
从而μ=EXi=1×0.3+1.2×0.2+1.5×0.5=1.29，
σ2=DXi=（1-1.29）2×0.3+（1.2-1.29）2×0.2+（1.5-1.29）2×0.5=0.0489，于是，由列维-林德伯格中心极限定理得
（2）记Y是售出的价格为1.2（元）的蛋糕块数，则Y～B（300，0.2）.于是由棣莫弗-拉普拉斯中心极限定理知，
有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章
- 详细阅读
-
大数定律及其在风险管理与保险中的应用详细阅读
大数定律阐述了大量随机现象平均结果的稳定性，即在随机现象大量重复出现时，偶然性的相互抵消几乎成为必然，随着试验次数的增多，事件发生的频率逐渐稳定于某个常数。保险领域的大数定律的基本含义是，当同质的风险单位数量越多，实际损失的结果会越接近从无限风险单位数量中得出的预期损失。依据大数定律，随着观测样本的增加，对均值的相对偏差就会越小，即样本数量越大，对预期损失的估计波动就越小。......
2023-08-11
-
函数极限与左、右极限关系详细阅读
【主要内容】1.设函数f（x）在点x0的某个去心邻域内有定义，则limx的充分必要条件是注 （ⅰ）对任意ε>0，如果存在δ>0，当0<|x-x0|<δ时有|f（x）-A|<ε.对任意ε>0，存在δ>0，使得-δ
2023-10-27
-
极限理论与ε-语言详解详细阅读
用“ε-语言”讲述极限概念，可以表述得十分严格。但是，用“ε-语言”定义极限，逻辑结构显得相当复杂。100多年来，“ε-语言”始终占据着微积分的课堂。要真正掌握微积分的原理，就不得不过“ε-语言”这一关。极限的“ε-语言”，既是打开微积分宝库的钥匙，又是阻拦人们获取宝库珍宝的关卡！人们似乎已形成了一种认识：不使用“ε-语言”，就谈不上严格地讲授微积分。......
2023-10-17
-
古德定律与成功法则对话详细阅读
这一观点后来被人称为古德定律。当曹操就这件事征求贾翊的意见时，贾翊却一声不吭。曹操和齐高帝所提的问题对于下属来说可谓是非常棘手，稍有不慎就会引起龙颜大怒。而贾翊和王僧虔没有正面的回答问题，这一点相当聪明，既避免了冒犯领导权威，也没有给人阿谀奉承的感觉。2．不批评、不责备、不抱怨、不攻击、不说教：反之只会使事情恶化，成为沟通的刽子手。......
2023-12-01
-
安培定律：发现电与磁的联系详细阅读
安培定律寻找电与磁的联系安培定律在探索电与磁相互转化的物理学史上，占据着举足轻重的地位。并且安培定律中有一个非常好玩的规则，那就是通过手指的指向来判断磁感线的方向。安培定律为何会有如此神奇的力量呢？安培定律不仅决定了磁场的性质，还提供了计算电流相互作用的途径，是研究磁作用的基本实验定律，对电磁学有着极其重要的意义。......
2024-06-12
-
极限与配合的标注技巧详细阅读
极限与配合是尺寸标注中的一项重要技术要求。上极限偏差上极限尺寸与公称尺寸的代数差。零线表示公称尺寸的一条直线，以其为基准确定偏差和公差。国家标准还规定，一般情况下优先采用基孔制配合。配合代号是在公称尺寸后面用分数形式注写的。......
2023-06-28
-
合力矩定理的应用与解析详细阅读
讨论合力对某点的矩和分力对该点的矩的关系，就是我们下面要讲述的合力矩定理。图3-17力矩投影由图3-17 可以看出将上述等式两边相加，有根据合力投影定理，有于是定理得到证明。对于有合力的其他各种力系，合力矩定理也是成立的。求啮合力Fn 对轮心点O 的矩。......
2023-06-19
相关推荐