首页理论教育切比雪夫不等式：估计随机变量X的概率超过特定区间

切比雪夫不等式：估计随机变量X的概率超过特定区间

2025-09-30 理论教育版权反馈

【摘要】：【主要内容】切比雪夫不等式设随机变量X的数学期望EX和方差DX都存在，则对任意ε>0，有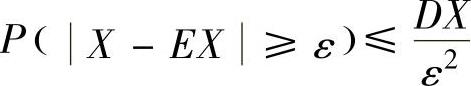或切比雪夫不等式可以用来估计某个随机变量X（仅知EX与DX，而未知X的分布）在以EX为中心的对称区间上取值的概率.【典型例题】例7.19.1 从发芽率为0.95的一批种子里随机取400粒，用切比雪夫不等式估计其不发芽的种子在15粒与25粒之间的概率.精解设随机变量X为400粒种子中不发芽的种子数，则X～B（4

【主要内容】

切比雪夫不等式

设随机变量X的数学期望EX和方差DX都存在，则对任意ε>0，有或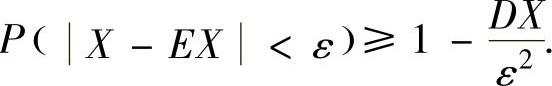

切比雪夫不等式可以用来估计某个随机变量X（仅知EX与DX，而未知X的分布）在以EX为中心的对称区间上取值的概率.

【典型例题】

例7.19.1 从发芽率为0.95的一批种子里随机取400粒，用切比雪夫不等式估计其不发芽的种子在15粒与25粒之间的概率.

精解设随机变量X为400粒种子中不发芽的种子数，则X～B（400，0.05），并且EX=400×0.05=20，DX=400×0.05×（1-0.05）=19，于是由切比雪夫不等式知

例7.19.2 设随机变量X，Y的数学期望分别为-2，2，方差分别为1，4，而相关系数为-0.5.用切比雪夫不等式估计概率P（X+Y≥6）.

精解记Z=X+Y，则

EZ=EX+EY=0，

所以，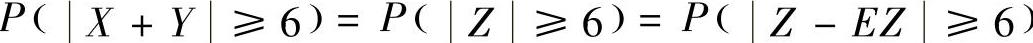

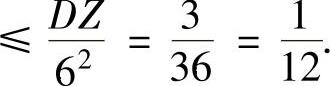
例7.19.3 设随机变量X～N（1，1），Y～N（0，1），且E（XY）=-0.1.用切比雪夫不等式估计概率P（-4<X+2Y<6）.(https://www.chuimin.cn)

精解记Z=X+2Y，则

EZ=EX+2EY=1+2×0=1，

DZ=DX+4DY+4Cov（X，Y）

=1+4×1+4[E（XY）-EX·EY]

=5+4（-0.1-1×0）=4.6，

所以，由切比雪夫不等式得

例7.19.4 设二维随机变量（X，Y）在圆域D：x²+y²≤4上服从均匀分布，用切比雪夫不等式估计概率P（XY≥1）.

精解应先算E（XY）与D（XY），由（X，Y）的概率密度为f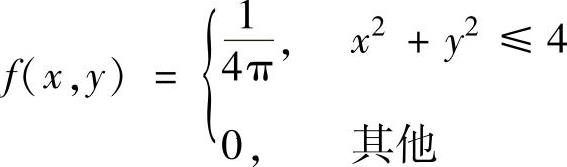，知

D（XY）=E（XY-E（XY））2=E（X²Y²）

由于（X，Y）在D上服从均匀分布，所以P（XY≥1）=P（XY≤-1），从而