,Xn)是n维随机变量,则称F(x1,x2,…,Xn)的分布函数或X1,X2,…......
2023-10-27
【主要内容】
(1)离散型情形设X是离散型随机变量,它的分布律为P(X=xi)=pi(i=1,2,…).如果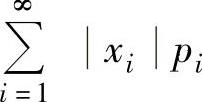
收敛,则称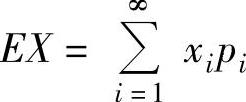 为X的数学期望.
为X的数学期望.
(2)连续型情形设X是连续型随机变量,它的概率密度为f(x)(-∞<x<+∞).如果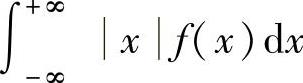
收敛,则称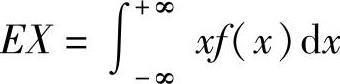 为X的数学期望.
为X的数学期望.
2.随机变量函数的数学期望
(1)离散型情形
设X是离散型随机变量,它的分布律为P(X=xi)=pi(i=1,2,…),又设g(x)是连
续函数,则X的函数g(X)的数学期望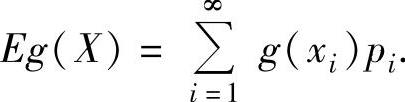
设(X,Y)是二维离散型随机变量,它的分布律为P(X=xi,Y=yi)=pij(i=1,2,…;j=1,2,…),又设h(x,y)是连续函数,则X,Y的函数h(X,Y)的数学期望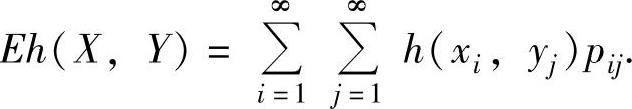
(2)连续型情形
设X是连续型随机变量,它的概率密度为f(x)(-∞<x<+∞),又设g(x)是连续函数,则X的函数g(X)的数学期望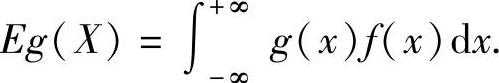
设(X,Y)是二维连续型随机变量,它的概率密度为f(x,y)(-∞<x<+∞,-∞<y<+∞),又设h(x,y)是连续函数,则X,Y的函数h(X,Y)的数学期望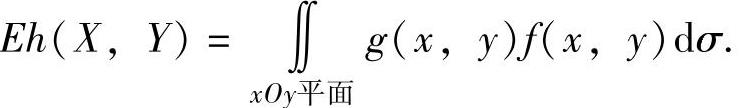
3.数学期望的性质
设X,Y是随机变量,c,c1,c2是常数,则
(1)Ec=c;
(2)E(c1X+c2Y)=c1EX+c2EY;
(3)当X与Y相互独立时,E(XY)=EX·EY.
4.常用随机变量的数学期望
设X服从0-1分布,则EX=p;
设X~B(n,p),则EX=np;
设X~π(λ),则EX=λ;
设X~U(a,b),则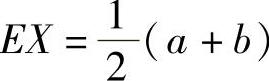 ;
;
设X~E(λ),则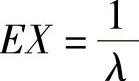 ;
;
设X~N(μ,σ2),则EX=μ.
【典型例题】
例7.16.1 将3只球随机地放入编号为1,2,3,4的四个盒中,以X表示有球盒的最大号码,求EX.
精解 先计算X的分布律.
X全部可能取的值为1,2,3,4,对应的概率为
P(X=1)=P{3只球全部放入1号盒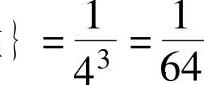 ,
,
P(X=2)=P{3只球中至少有1只放入2号盒,而其余的全放入1号盒}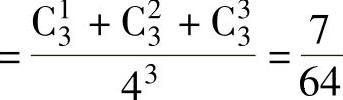 ,
,
P(X=3)=P{3只球中至少有1只放入3号盒,而其余的全放入1号盒或2号盒}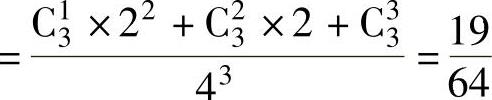 ,
,
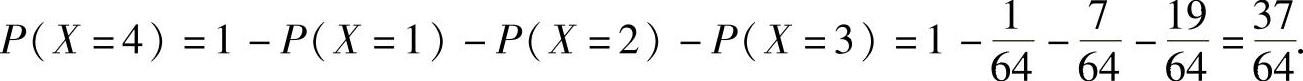
所以由数学期望的定义得
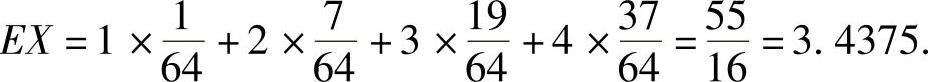
例7.16.2 某车站每天8:00~9:00,9:00~10:00都恰有一辆客车到站,但到站时刻是随机的,且两个时间区间里到站时刻相互独立,具体规律如下:
 (www.chuimin.cn)
(www.chuimin.cn)
今有一乘客于8:20到车站,求他候车时间X(单位:min)的数学期望.
精解 先写出X的分布律:
X可能取的值为10,30,50,70,90,为了计算对应的概率,记
A1={第一班车8:10到站}, A2={第一班车8:30到站},
A3={第一班车8:50到站}, B1={第二班车9:10到站},
B2={第二班车9:30到站}, B3={第二班车9:50到站},则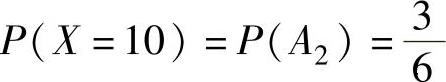 ,
,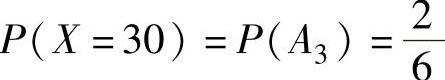 ,
,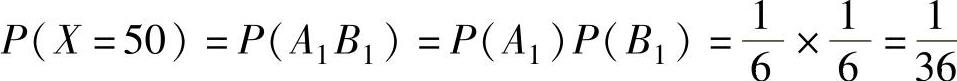 ,
,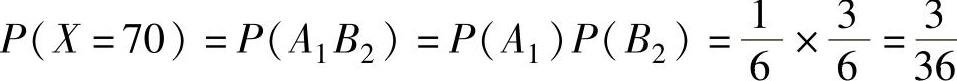 ,
,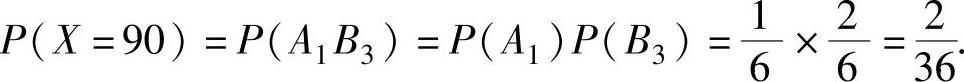 于是,
于是,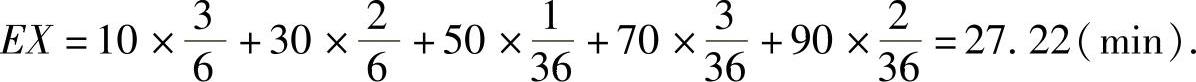
例7.16.3 设连续型随机变量的分布函数为
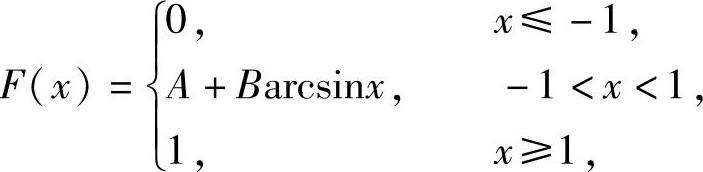
求EX.
精解 先确定常数A,B.
由于F(x)是连续型随机变量的分布函数,所以它是连续函数,特别在点x=-1,1处连续,于是有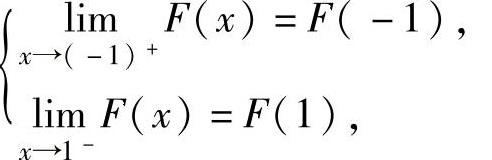 即
即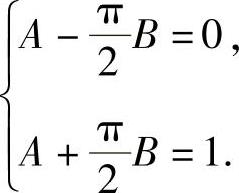
解此方程组得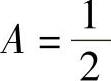 ,
, 因此
因此

由此得到X的概率密度
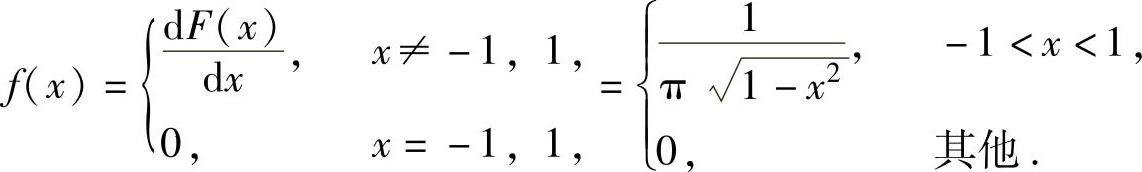
于是,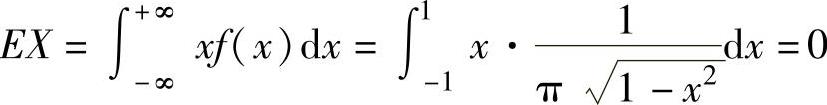 (对称区间上奇函数的积分为零).
(对称区间上奇函数的积分为零).
例7.16.4 设随机变量X与Y分别服从参数均为1的指数分布与泊松分布,求概率P(X2+Y2≤E(X+Y)).
精解 由于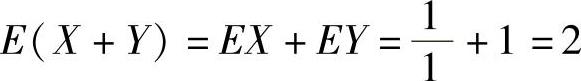 ,所以
,所以
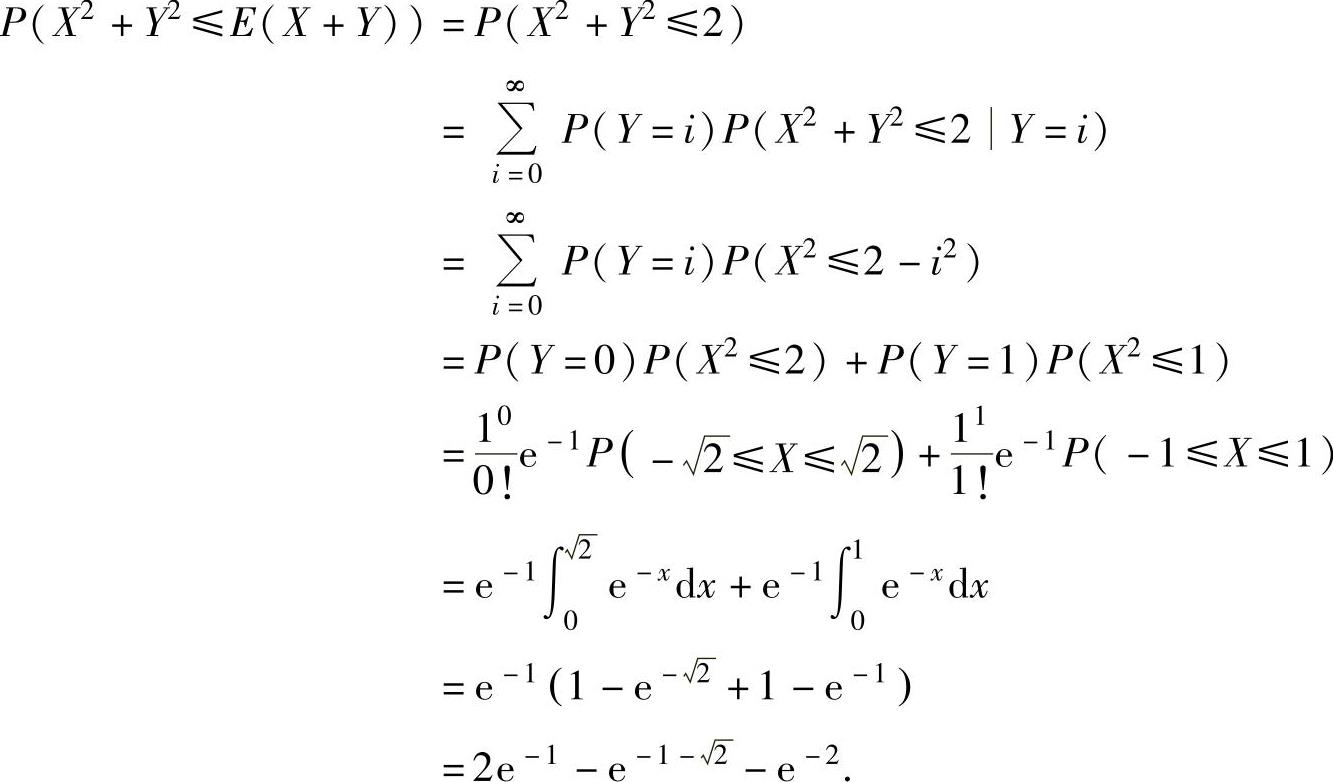
例7.16.5 设随机变量X与Y相互独立,且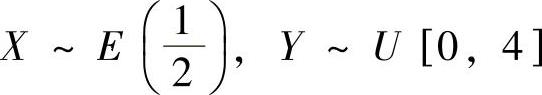 ,求
,求
E(min{X,Y})和E(X+XY+2).
精解 由题设知X与Y的概率密度分别为
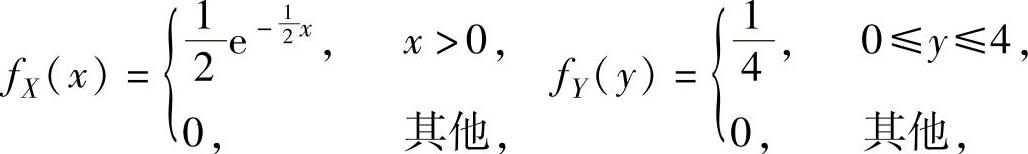
所以,由X与Y相互独立知二维随机变量(X,Y)的概率密度为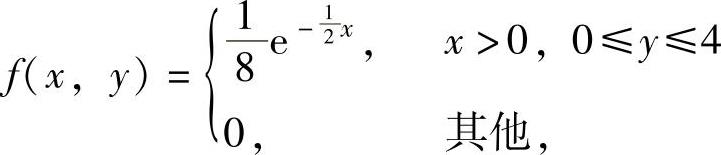 ,
,
即它在D={(x,y)x>0,0≤y≤4}(如图7.16.5阴影部分所示)上取值为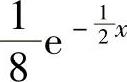 ,在xOy
,在xOy
平面的其他部分取值为零.
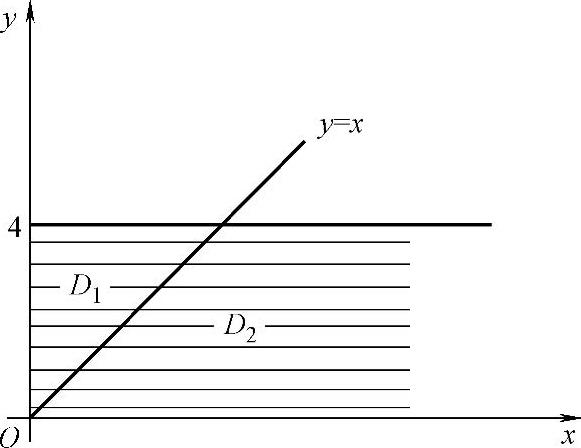
图 7.16.5
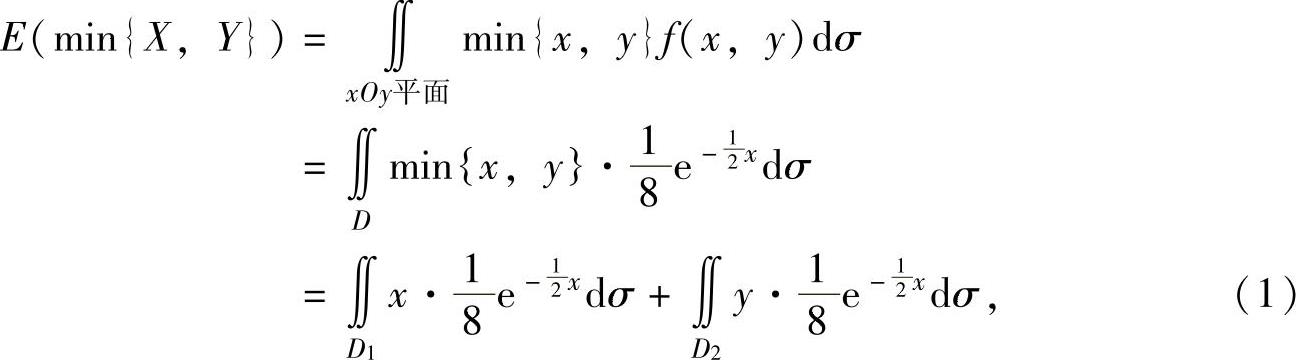
其中,D1与D2是D被直线y=x划分成的两部分,如图7.16.5所示,并且
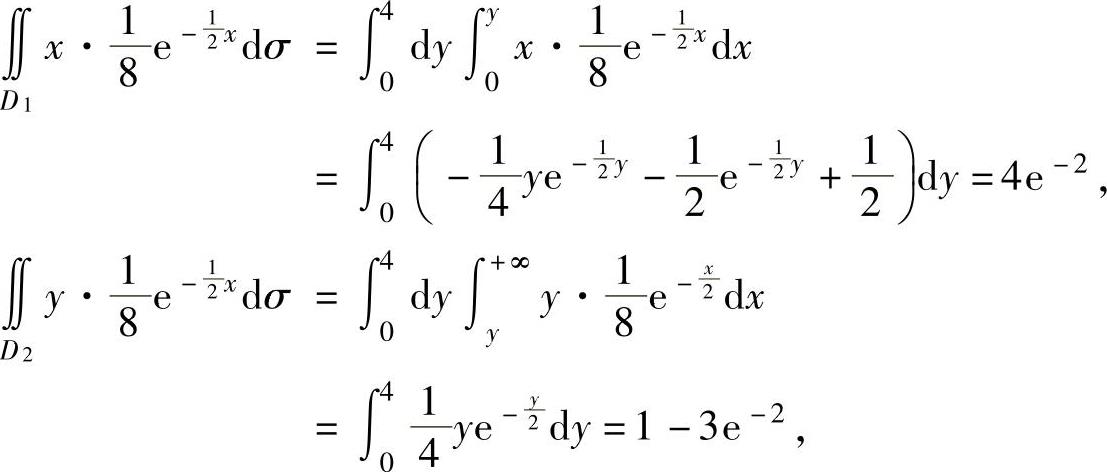
将它们代入式(1)得
E(min{X,Y})=4e-2+(1-3e-2)=1+e-2.下面计算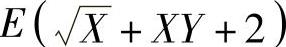

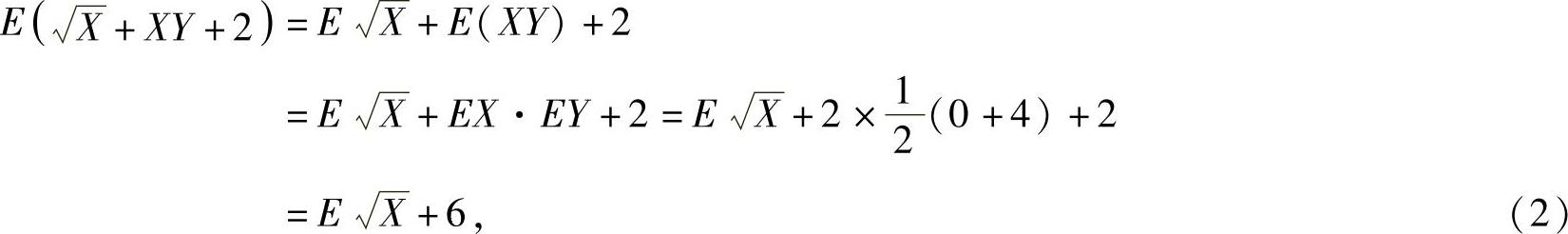
其中,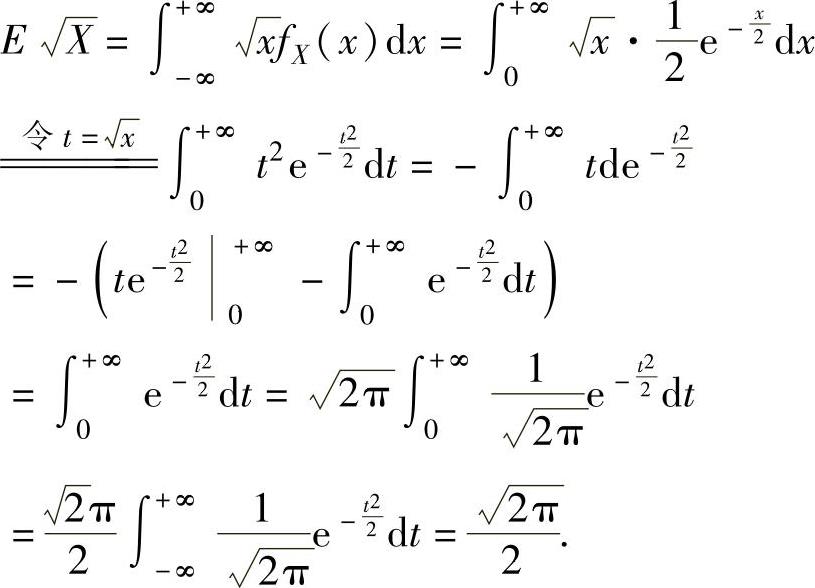
将它代入式(2)得
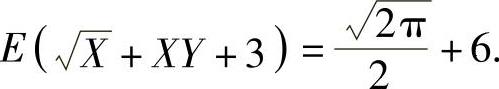
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

【主要内容】1.随机变量协方差的定义与性质设(X,Y)是二维随机变量.如果E[(X-EX)(Y-EY)]存在,则称Cov(X,Y)=E[(X-EX)(Y-EY)]为X与Y的协方差.协方差有以下性质:设X,X1,X2,Y是随机变量,则(1)Cov(X,Y)=Cov(Y,X);(2)Cov(X,c)=0(其中c是常数);(3)Cov(c1X,c2Y)=c1c2Cov(X,Y)(其中,c1,c2是常数)......
2023-10-27

数学文化的内涵的揭示,决定数学文化的教育价值的转变,影响教育工作者的教育观。所谓教育价值,是指教育对社会或个人等主体的存在或发展具有的意义或价值,数学文化的教育价值表现在科学方面的教育价值和人文方面的教育价值。从我国教育现实情况来看,视数学的教育价值过于工具性,体现在数学在各种考试文化中的核心和关键学科地位。......
2023-08-13

)为X的分布律,其中pi有以下性质:每个pi>0;Σipi=1.3.常用(一维)离散型随机变量及其分布律服从0-1分布的随机变量设随机变量X的分布律为,则称X是服从以p为参数的0-1分布的随机变量,简称X服从以p为参数的0-1分布,服从二项分布的随机变量设随机变量X的分布律为P(X=k)=Cknpk(1-p)n-k(k=0,1,2,…......
2023-10-27

1.二元随机变量函数分布的计算设(X,Y)是二维随机变量,g(x,y)是已知函数,则称随机变量Z=g(X,Y)为两个随机变量的函数.当(X,Y)是二维离散型随机变量,其分布列为P=pij(i=1,2,…......
2023-10-27

圆的周长是其自身外围曲线的长度。所以对π在从物理到统计的几乎每一个领域的频繁出现,我们无须感到惊讶。1995年,西蒙·普劳夫找到一个可以计算出π的任意一个数位上的数字的方法,并且无须计算出这个数位之前的其他所有数字。参考阅读//No. 4 极限,第12页No. 30 超越数,第64页No. 59 欧几里得空间,第122页右图:π有着许多不寻常的数学性质。数字π是圆形周长与直径的比值,所有的圆的π值都一样。......
2023-11-22

),且取这些值对应的概率为pij(i=1,2,…),p·j=Σipij(j=1,2,…).4.二维离散型随机变量的条件分布律设(X,Y)是二维离散型随机变量,它的分布律及边缘分布律分别为P=pij(i=1,2,…......
2023-10-27
相关推荐