首页 理论教育二元随机变量函数的分布及解析

二元随机变量函数的分布及解析

2023-10-27 理论教育 版权反馈
【摘要】：1.二元随机变量函数分布的计算设（X，Y）是二维随机变量，g（x，y）是已知函数，则称随机变量Z=g（X，Y）为两个随机变量的函数.当（X，Y）是二维离散型随机变量，其分布列为P=pij（i=1，2，…

【主要内容】

1.二元随机变量函数分布的计算

设（X，Y）是二维随机变量，g（x，y）是已知函数，则称随机变量Z=g（X，Y）为两个随机变量的函数.

当（X，Y）是二维离散型随机变量，其分布列为P（X=xi，Y=yj）=pij（i=1，2，…，m，…；j=1，2，…，n，…）时，Z=g（X，Y）的分布律为

978-7-111-46245-3-Part03-397.jpg

这里z1，z2，…，zk，…确定如下：对每对（xi，yj）算出g（xi，yj）的值，然后将它们整合，即相同的只保留一个，并作由小到大的排列.此外，

978-7-111-46245-3-Part03-398.jpg

由此可以进一步算出Z的分布函数FZ（z）.

当（X，Y）是二维连续型随机变量，其概率密度为f（x，y）时，随机变量Z=g（X，Y）的分布函数FZ（z）与概率密度fZ（z）可按以下方法计算：

978-7-111-46245-3-Part03-399.jpg

2.常见的两个随机变量函数的分布

（1）设（X，Y）是二维连续型随机变量，其概率密度为f（x，y），则随机变量Z=aX+bY+c（a，b，c是常数）的概率密度fZ（z）为

当b≠0时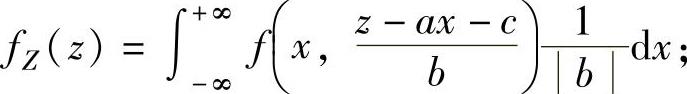，978-7-111-46245-3-Part03-400.jpg

当a≠0时，978-7-111-46245-3-Part03-401.jpg

注 （ⅰ）当Z=X+Y时，978-7-111-46245-3-Part03-402.jpg，特别地，当

X与Y相互独立时，978-7-111-46245-3-Part03-403.jpg（其中，fX（x）和fY（y）分别是X和

Y的概率密度）.

（ⅱ）当Z=X-Y时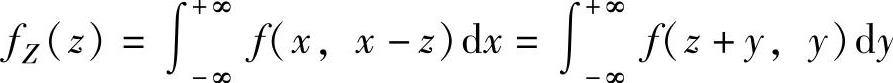，978-7-111-46245-3-Part03-404.jpgy，特别地，当X与

Y相互独立时，978-7-111-46245-3-Part03-405.jpg（其中，fX（x）和fY（y）分别是X和

Y的概率密度）.

（2）设X与Y相互独立，它们的分布函数分别为FX（x）与FY（y），则随机变量Z1=max{X，Y}与Z2=min{X，Y}的分布函数分别为

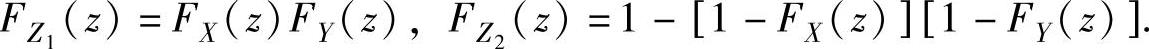
978-7-111-46245-3-Part03-406.jpg

【典型例题】

例7.14.1 设随机变量X与Y相互独立，它们的分布律分别为

978-7-111-46245-3-Part03-407.jpg

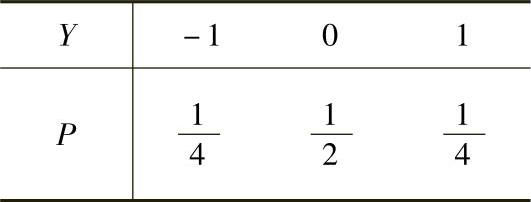
978-7-111-46245-3-Part03-408.jpg

求随机变量Z=X+2Y的分布律.

精解 先写出（X，Y）的分布律，然后据此确定Z的分布律.

由于X与Y相互独立，所以（X，Y）的分布律为

978-7-111-46245-3-Part03-409.jpg

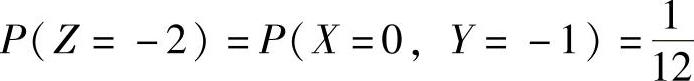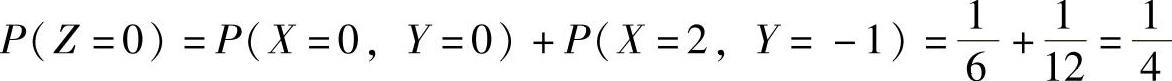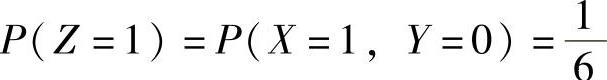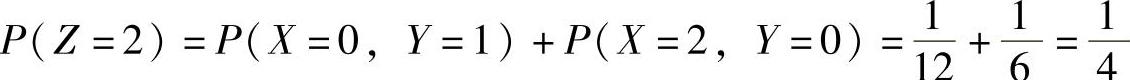由上表可知Z=X+2Y全部可能取的值为-2，-1，0，1，2，3，4，并且对应的概率为978-7-111-46245-3-Part03-410.jpg，978-7-111-46245-3-Part03-411.jpg，978-7-111-46245-3-Part03-412.jpg，978-7-111-46245-3-Part03-413.jpg，978-7-111-46245-3-Part03-414.jpg，978-7-111-46245-3-Part03-415.jpg，978-7-111-46245-3-Part03-416.jpg，

因此Z=X+2Y的分布律可列表表示为

978-7-111-46245-3-Part03-417.jpg

例7.14.2 设随机变量（X，Y）的概率密度为

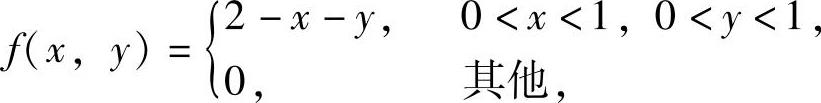
978-7-111-46245-3-Part03-418.jpg

求随机变量Z=X+Y的概率密度fZ（z）.

精解 按Z=X+Y的概率密度计算公式计算fZ（z），即

978-7-111-46245-3-Part03-419.jpg

，(www.chuimin.cn)

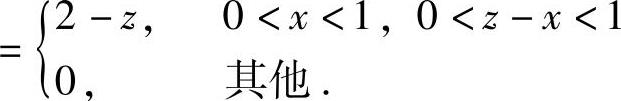其中，978-7-111-46245-3-Part03-420.jpg，978-7-111-46245-3-Part03-421.jpg，

由此可知，f（x，z-x）在D={（x，z）0<x<1，0<z-x<1}（如图7.14.2阴影部分所示）上取值为2-z，在xOz平面的其他部分取值都为零.

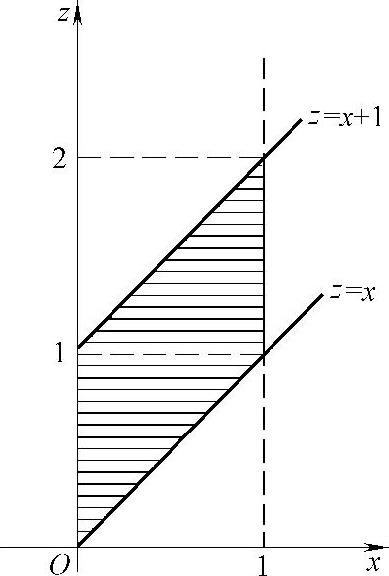
978-7-111-46245-3-Part03-422.jpg

图 7.14.2

当0≤z<1时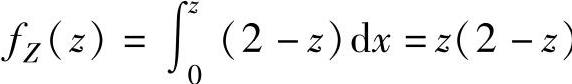，978-7-111-46245-3-Part03-423.jpg，

当1≤z≤2时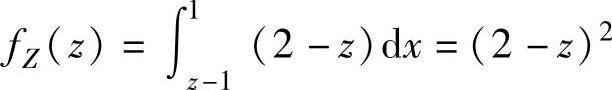，978-7-111-46245-3-Part03-424.jpg，

当z<0或z>2时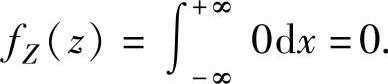，978-7-111-46245-3-Part03-425.jpg

因此978-7-111-46245-3-Part03-426.jpg

例7.14.3 设二维随机变量（X，Y）的概率密度为

978-7-111-46245-3-Part03-427.jpg

求随机变量Z=2X-Y的概率密度fZ（z）.

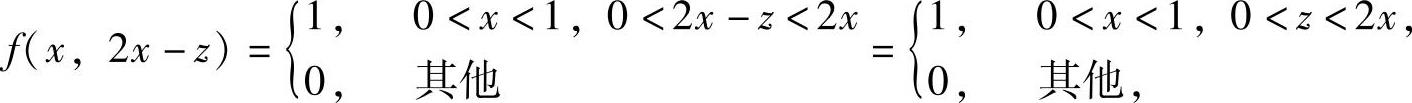
精解 按Z=2X-Y的概率密度计算公式计算fZ（z），即978-7-111-46245-3-Part03-428.jpg，其中，978-7-111-46245-3-Part03-429.jpg

即f（x，2x-z）在D={（x，z）0<x<1，0<z<2x}（如图7.14.3阴影部分所示）上取值为1，在xOz平面的其他部分上取值为零.

978-7-111-46245-3-Part03-430.jpg

图 7.14.3

当0≤z≤2时，

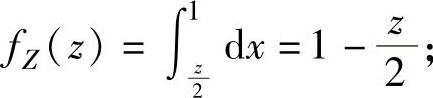
978-7-111-46245-3-Part03-431.jpg

当z<0或z>2时，

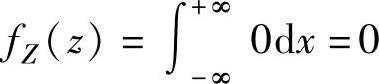
978-7-111-46245-3-Part03-432.jpg

，

即978-7-111-46245-3-Part03-433.jpg

例7.14.4 设随机变量X与Y相互独立，X～E（1），Y～U[0，1].

（1）求随机变量Z=max{X，Y}的概率密度fZ（z）；

（2）记U=min{X，Y}，求概率978-7-111-46245-3-Part03-434.jpg

精解 （1）先算Z的分布函数FZ（z），然后求导得到fZ（z）.

由于X与Y相互独立，所以FZ（z）=FX（z）FY（z），（1）

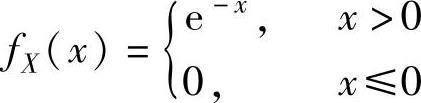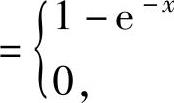
其中，由X的概率密度978-7-111-46245-3-Part03-435.jpg，得X的分布函数978-7-111-46245-3-Part03-436.jpg978-7-111-46245-3-Part03-437.jpg

，x>0

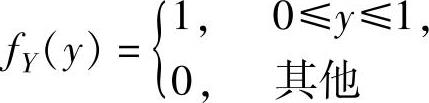
{x≤0，从而978-7-111-46245-3-Part03-438.jpg由Y的概率密度978-7-111-46245-3-Part03-439.jpg

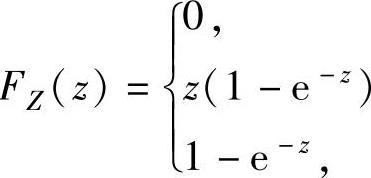
得Y的分布函数978-7-111-46245-3-Part03-440.jpg，从而978-7-111-46245-3-Part03-441.jpg，所以978-7-111-46245-3-Part03-442.jpg

z<0，，0≤z≤1，

z>1.

由此得到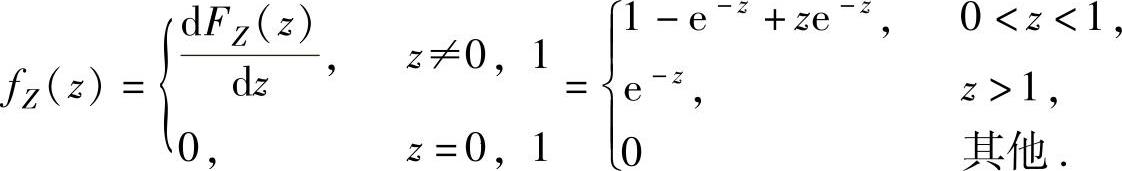，978-7-111-46245-3-Part03-443.jpg

（2）先计算U的分布函数FU（u），然后由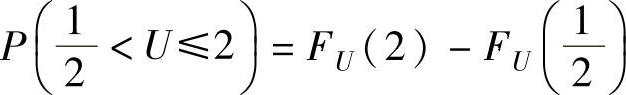978-7-111-46245-3-Part03-444.jpg算出这个概

率.由于U=min{X，Y}的分布函数

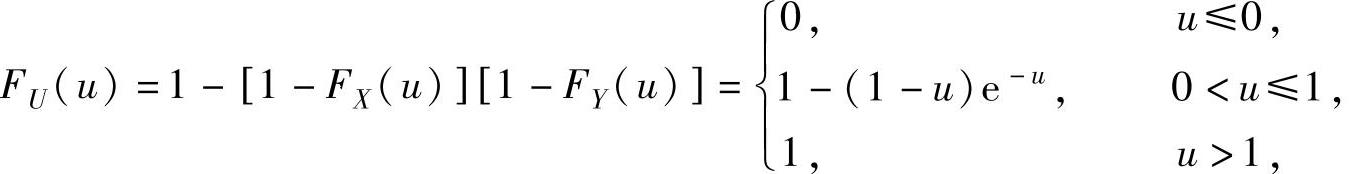
978-7-111-46245-3-Part03-445.jpg

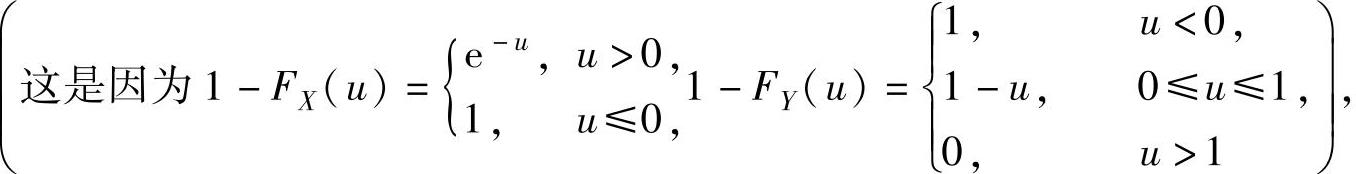
978-7-111-46245-3-Part03-446.jpg

所以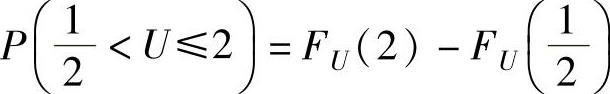，978-7-111-46245-3-Part03-447.jpg978-7-111-46245-3-Part03-448.jpg

有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章

  • 随机变量函数的分布，全面复习与常考知识点解析 随机变量函数的分布，全面复习与常考知识点解析

    设随机变量X的分布已知，则称X的函数Y=g的分布为（一元）随机变量函数的分布.1.离散型情形设X是离散型随机变量，其分布律为则 Y=g的分布律可按以下步骤计算：计算Y全部可能取的值g，g，…，g，有相同的只取其中一个，然后将它们由小到大排列，记为y1，y2，…，k）都作同样处理，就可确定Y取y1，y2，…......

    2023-10-27

    详细阅读
  • 二维随机变量分布函数考研数学常考知识点解析 二维随机变量分布函数考研数学常考知识点解析

    ，Xn）是n维随机变量，则称F（x1，x2，…，Xn）的分布函数或X1，X2，…......

    2023-10-27

    详细阅读
  • 2015考研数：一维随机变量的分布函数简介 2015考研数：一维随机变量的分布函数简介

    ）时，X的分布函数F当X的分布函数为F，其中x1，x2，…......

    2023-10-27

    详细阅读
  • 解析函数概念|复变函数及应用 解析函数概念|复变函数及应用

    解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下：定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......

    2023-10-30

    详细阅读
  • 离散型随机变量及其分布律解析 离散型随机变量及其分布律解析

    ）为X的分布律，其中pi有以下性质：每个pi>0；Σipi=1.3.常用（一维）离散型随机变量及其分布律服从0-1分布的随机变量设随机变量X的分布律为，则称X是服从以p为参数的0-1分布的随机变量，简称X服从以p为参数的0-1分布，服从二项分布的随机变量设随机变量X的分布律为P（X=k）=Cknpk（1-p）n-k（k=0，1，2，…......

    2023-10-27

    详细阅读
  • 随机变量概率分布简介 随机变量概率分布简介

    对于连续型随机变量，由于其可能取值无法一一列出，而且可以证明取个别值的概率等于零。因此连续型随机变量不存在分布律。此外，连续型随机变量也可用密度函数表示其统计规律。图X3.1频率密度图和频率分布图都会成为虚线表示的光滑曲线。前者称随机变量的概率密度曲线，后者称为随机变量的概率分布曲线。......

    2023-06-21

    详细阅读
  • 黄颊山雀：特征、分布及习性解析 黄颊山雀：特征、分布及习性解析

    中文名 黄颊山雀拉丁名 Parus spilonotus英文名 Yellow-cheeked Tit分类地位 雀形目山雀科体长 12～14cm体重 14～22g野外识别特征 小型鸟类，体色黑黄交错，具有明显的高耸羽冠，头顶、贯眼纹和胸腹中央纵纹黑色，头侧明黄色，上体黑色缀黄白斑，下体黄白色。常成对或小群活动，也和大山雀等其他小型鸟类混群，活跃地在乔灌木枝叶间飞翔跳跃。分布与居留分布于亚洲东南部地区。......

    2023-11-03

    详细阅读
  • 正弦函数性质及解析-机电应用数学 正弦函数性质及解析-机电应用数学

    由正弦函数y=sinx的图像可知：定义域正弦函数y=sinx的定义域是R.值域正弦函数y=sinx，x∈R的值域是[-1，1]，即对任意的x∈R，都有-1≤sinx≤1.其中，当，k∈Z，有ymax=1；当，k∈Z时，有ymin=-1.想一想等式2sinx=3，，都成立吗？例2求出下列函数的最大值和最小值：y=1-sinx； y=2sinx.解：当sinx=-1时，ymax=1-（-1）=2；当sinx=1时，ymin=1-1=0.当sinx=1时，ymax=2×1=2；sinx=-1时，ymin=2×（-1）=-2.想一想第题中的函数y=1-sinx取得最大值和最小值时，对应的x的取值集合分别是什么？......

    2023-11-22

    详细阅读