如前所述,大数定律揭示了大量随机变量的平均结果的稳定性,但没有涉及随机变量的分布。而中心极限定理则进一步揭示出大量相互独立的随机变量之和近似服从正态分布的一般规律,可以用于计算任一随机结果发生的具体概率。中心极限定理以严格的数学形式阐明了在大样本条件下,不论总体的分布如何,样本的均值总是近似地服从正态分布。这使得正态分布在数理统计中具有很重要的地位,并得到了广泛应用。......
2023-08-11
【主要内容】
设二维随机变量(X,Y)的分布函数为F(x,y),边缘分布函数为FX(x)和FY(y).如果对任意实数x,y有F(x,y)=FX(x)FY(y),则称X与Y相互独立(简称独立).
当(X,Y)是二维离散型随机变量,其分布律为P(X=xi,Y=yi)=pij(i=1,2,…,m,…;j=1,2,…,n,…),边缘分布律为P(X=xi)=pi·(i=1,2,…,m,…)和P(Y=yj)(j=1,2,…,n,…)时,X与Y相互独立的充分必要条件是对任意i,j都有
pij=pi··p·j
当(X,Y)是二维连续型随机变量,其概率密度为f(x,y)(-∞<x<+∞,-∞<y<+∞),边缘概率密度为fX(x)(-∞<x<+∞)和fY(y)(-∞<y<+∞)时,X与Y相互独立的充分必要条件是
f(x,y)=fX(x)fY(y)在xOy平面上几乎处处成立.
注 (ⅰ)设随机变量X与Y相互独立,g(x),h(y)是连续函数,则随机变量Z1=g(X)与Z2=h(Y)也相互独立.
(ⅱ)多个随机变量的独立性也可类似定义.
如果对任意实数x1,x2,…,xn有
F(x1,x2,…,xn)=F1(x1)F2(x2)…Fn(xn),则称随机变量X1,X2,…,Xn相互独立,其中F是n维随机变量(X1,X2,…,Xn)的分布函数,F1,F2,…,Fn分别是随机变量X1,X2,…,Xn的分布函数.
【典型例题】
例7.13.1 (单项选择题)设两个随机变量X与Y相互独立,且有相同的分布律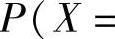
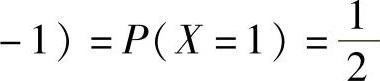 ,则下列等式中成立的是( ).
,则下列等式中成立的是( ).
A. B.P(X=Y)=1C.
B.P(X=Y)=1C.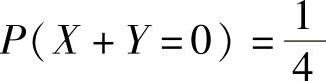 D.
D.
精解 先考虑选项A.
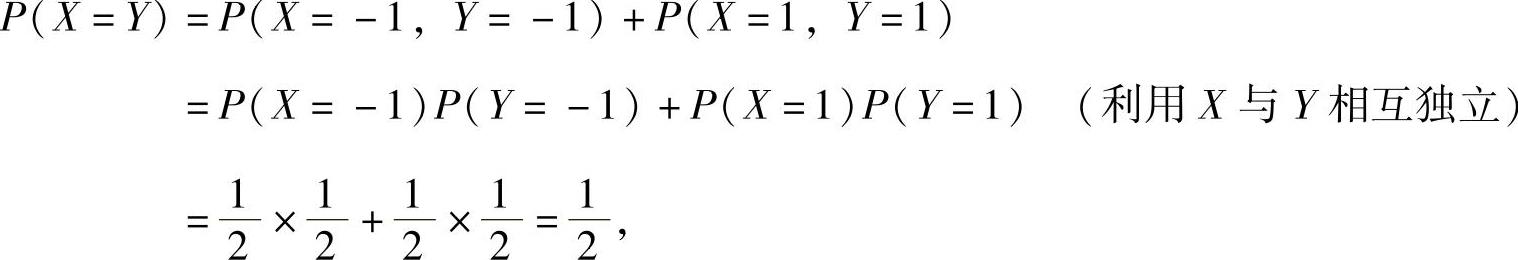
因此本题选A.
例7.13.2 设随机变量X与Y相互独立,二维随机变量(X,Y)的分布律及边缘分布律如下表所示:

求其中用文字表示的各个概率值.
精解 由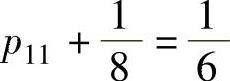 得
得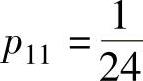 ;由
;由 得
得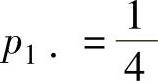 ;
;
由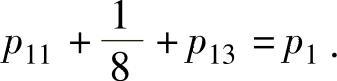 ,即
,即 得
得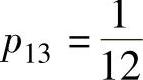 ;
;
由 ,即
,即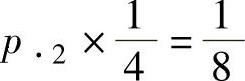 得
得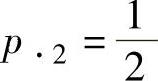 ;
;
由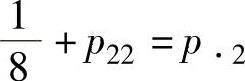 得
得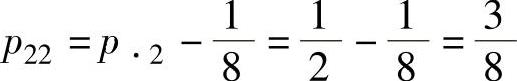 ;
;
由 p2·p·2=p22,即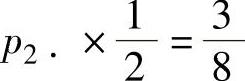 得
得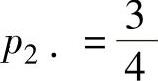 ;
;
由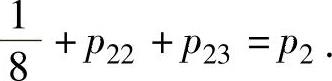 ,即
,即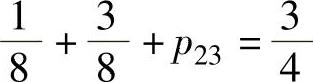 得
得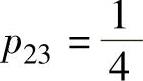 ,
,

例7.13.3 设随机变量X与Y相互独立,X~E(5),Y~U[0,2],求:
(1)二维随机变量(X,Y)的概率密度f(x,y);
(2)概率P(Y≥X).
精解 (1)由题设知,X与Y的概率密度分别为(www.chuimin.cn)
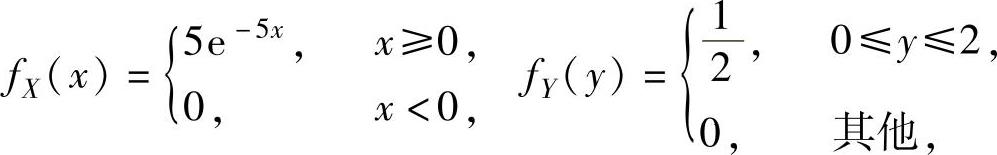
所以,由X与Y相互独立得(X,Y)的概率密度为
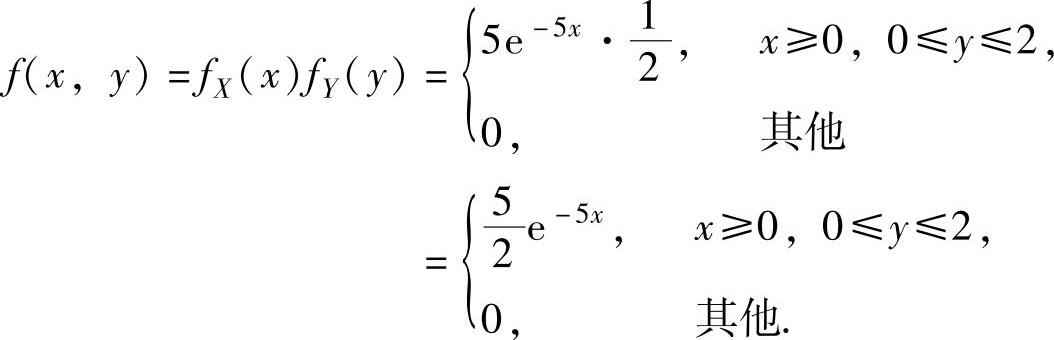
(2)由(1)知,f(x,y)在D={(x,y)x≥0,0≤y≤2}(如图7.13.3阴影部分所示)上取值为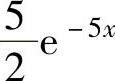 ,在xOy平面的其他部分取值为零.P(Y≥X)=P((X,Y)∈D1)(其中D1={(x,y)y≥x})
,在xOy平面的其他部分取值为零.P(Y≥X)=P((X,Y)∈D1)(其中D1={(x,y)y≥x})
=P((X,Y)∈D∩D1=△OAB)(△OAB如图7.13.3所示)
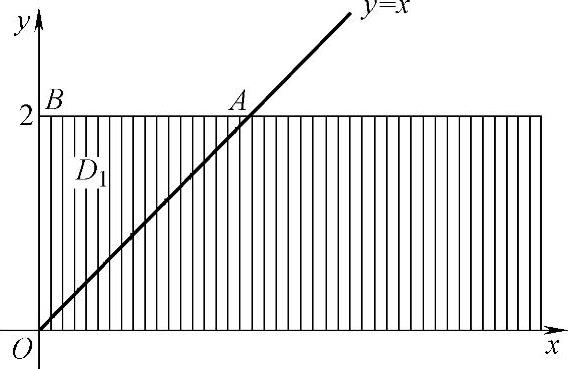
图 7.13.3
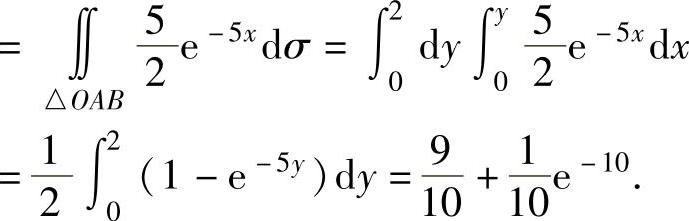
例7.13.4 设随机变量X与Y相互独立,又设随机变量Z在[0,1]上随机取值,当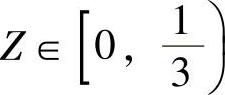 时,X与Y都服从U[0,1];当
时,X与Y都服从U[0,1];当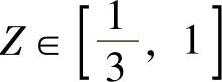 时,X与Y都服从B(2,0.8),求关
时,X与Y都服从B(2,0.8),求关
于t的二次方程t2+Xt+Y=0有实根的概率.
精解 记A={所给二次方程有实根},则

当X,Y都服从U[0,1]时,它们的概率密度分别为
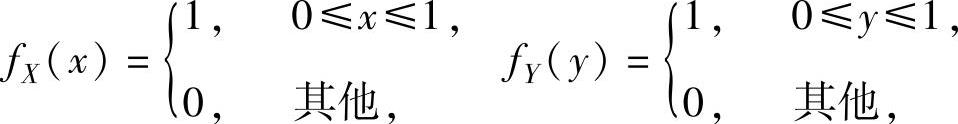
所以,由X与Y相互独立得(X,Y)的概率密度为
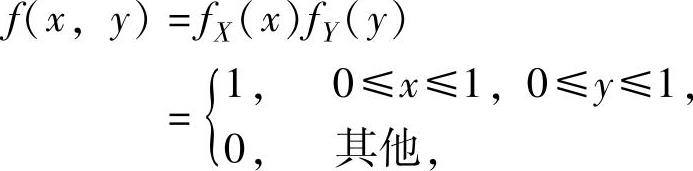
由此得到

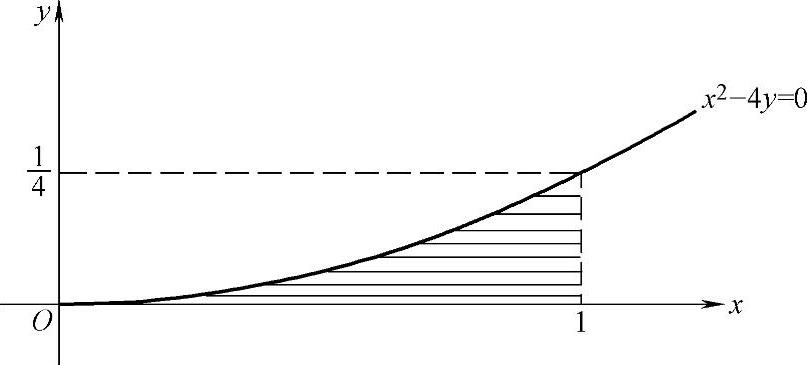
图 7.13.4
当X,Y都服从B(2,0.8)时,它们的分布律分别为
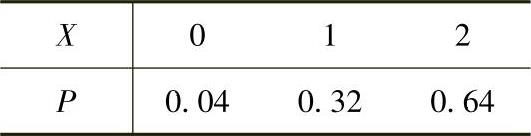
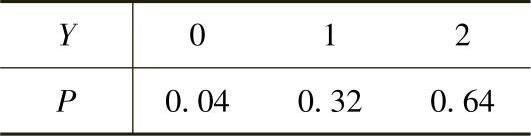
所以,由X与Y相互独立得
p2=P((X,Y)∈D)=P(X=0,Y=0)+P(X=1,Y=0)+P(X=2,Y=0)+P(X=2,Y=1)
=P(X=0)P(Y=0)+P(X=1)P(Y=0)+P(X=2)P(Y=0)+P(X=2)P(Y=1)
=0.04×0.04+0.32×0.04+0.64×0.04+0.64×0.32
=0.2448.(3)
将式(2)、式(3)代入式(1)得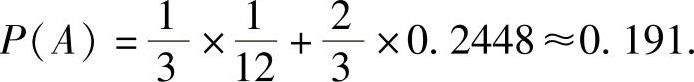
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

如前所述,大数定律揭示了大量随机变量的平均结果的稳定性,但没有涉及随机变量的分布。而中心极限定理则进一步揭示出大量相互独立的随机变量之和近似服从正态分布的一般规律,可以用于计算任一随机结果发生的具体概率。中心极限定理以严格的数学形式阐明了在大样本条件下,不论总体的分布如何,样本的均值总是近似地服从正态分布。这使得正态分布在数理统计中具有很重要的地位,并得到了广泛应用。......
2023-08-11

图4-51 分组重复排列的韵律构图重复韵律的构图中元素数量多为两个以上元素间的构图关系,重复韵律的构图多数都存在对称关系或镜像关系。图4-54所示构图中元素的颜色、体量、形状均不同,但根据相似的分组方式,同样具有重复韵律关系。由此可得出结论,在差异元素分组重复韵律构图中,元素的颜色、位置是重要的视觉分组要素。......
2023-08-24

我们将这种随试验结果的不同而取不同值的变量称随机变量,记X、Y、Z等。水文上连续型随机变量是常见的,如年径流量、年降水量、年最大洪峰流量等均是连续型随机变量。......
2023-06-21

【主要内容】1.随机变量协方差的定义与性质设(X,Y)是二维随机变量.如果E[(X-EX)(Y-EY)]存在,则称Cov(X,Y)=E[(X-EX)(Y-EY)]为X与Y的协方差.协方差有以下性质:设X,X1,X2,Y是随机变量,则(1)Cov(X,Y)=Cov(Y,X);(2)Cov(X,c)=0(其中c是常数);(3)Cov(c1X,c2Y)=c1c2Cov(X,Y)(其中,c1,c2是常数)......
2023-10-27

眼见为实,耳听为虚。做人一定要有自己的想法,不能人云亦云,否则就很容易被误导,从而犯错。这些虽然都是生活中的小事,但却是培养孩子独立性的重要内容。父母的一举一动,还有父母的品质,都是孩子模仿和学习的榜样。对于男孩来说,他们更富有个性,喜欢张扬,常常能想出与众不同的做事方法,而这种与众不同就是创造。这样一来,男孩在一些事情上就会形成自己的见解。男孩在思考的过程中,就会慢慢有了自己的思路和解决方法。......
2023-12-03

随机变量的概率分布完整地刻划了随机变量的统计规律。这种从侧面说明随机变量统计特性的某些特征数字,称为随机变量的统计参数。图X3.3Cv对密度曲线的影响图X3.4Cs对密度曲线的影响称Cv为样本变差系数或离势系数、离差系数,其式中,称为模比系数。......
2023-06-21

汪曾祺的两个年代及其他一、《邂逅集》光芒难掩祖籍安徽,但出生于江苏高邮,作品也多以高邮为背景的汪曾祺,青年时代就读于抗战时期最高学府“西南联大”中国文学系,亲聆梅贻琦、刘文典、杨振声、朱自清、罗常培、冯友兰、闻一多、金岳霖、吴宓、唐兰等名师教诲①,小说创作更得沈从文悉心指导,和略早成名的穆旦及另外三位后来所谓“九叶诗人”一样,是“联大”八年在文学创作上结出的硕果。......
2024-01-11

对于连续型随机变量,由于其可能取值无法一一列出,而且可以证明取个别值的概率等于零。因此连续型随机变量不存在分布律。此外,连续型随机变量也可用密度函数表示其统计规律。图X3.1频率密度图和频率分布图都会成为虚线表示的光滑曲线。前者称随机变量的概率密度曲线,后者称为随机变量的概率分布曲线。......
2023-06-21
相关推荐