首页 理论教育二维连续型随机变量条件概率计算精要

二维连续型随机变量条件概率计算精要

2023-10-27 理论教育 版权反馈
【摘要】：【主要内容】设二维连续型随机变量（X，Y）的概率密度为f（x，y），则两类条件概率P（a0）和P（a0）可以分别按以下公式计算：（1）；（2）（其中，fYX（yc）是在X=c的条件下，Y的条件概率密度）.【典型例题】例7.12.1 设二维随机变量（X，Y）的概率密度为求条件概率精解 f

【主要内容】

设二维连续型随机变量（X，Y）的概率密度为f（x，y），则两类条件概率P（a<Y≤b X≤c）（其中，P（X≤c）>0）和P（a<Y≤bX=c）（其中，边缘概率密度fX（x）在点x=c处的值fX（c）>0）可以分别按以下公式计算：

（1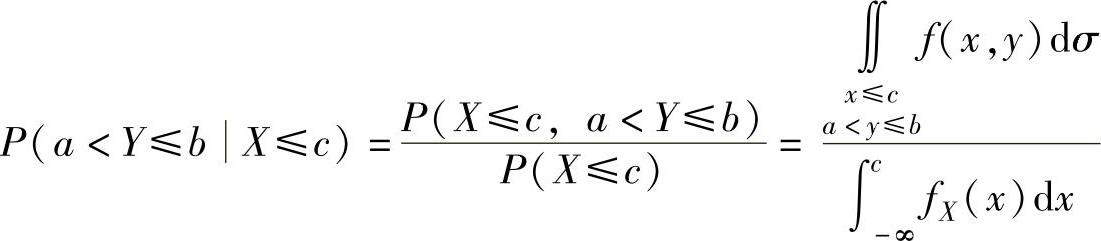）978-7-111-46245-3-Part03-320.jpg；

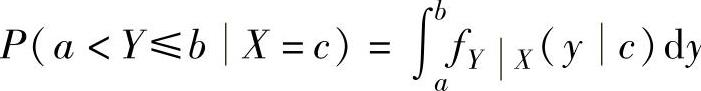（2）978-7-111-46245-3-Part03-321.jpg（其中，fYX（yc）是在X=c的条件下，Y的

条件概率密度）.

【典型例题】

例7.12.1 设二维随机变量（X，Y）的概率密度为

978-7-111-46245-3-Part03-322.jpg

求条件概率978-7-111-46245-3-Part03-323.jpg

精解 f（x，y）仅在区域G={（x，y）0<x<1，0<y<2x}（如图7.12.1阴影部分所示）内取值为1，在xOy平面的其他部分都取值为零.

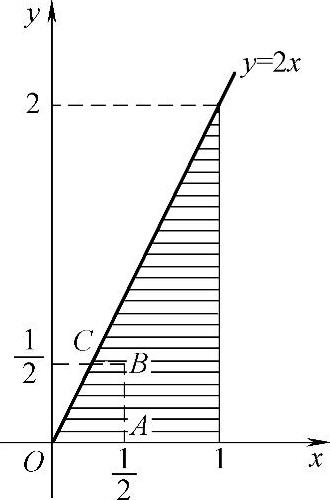
978-7-111-46245-3-Part03-324.jpg

图 7.12.1

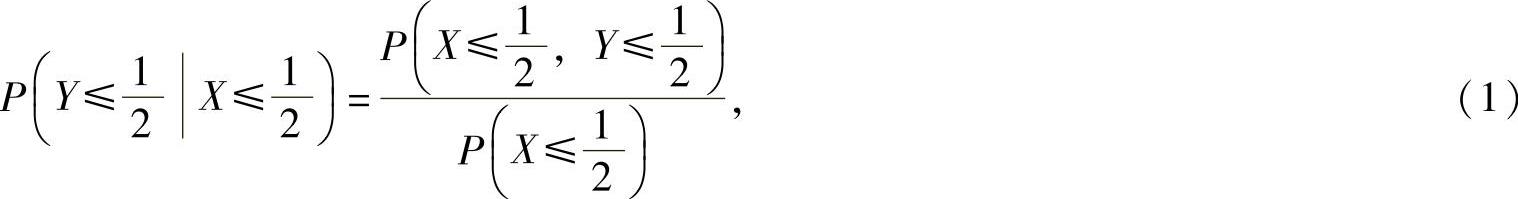
由于978-7-111-46245-3-Part03-325.jpg

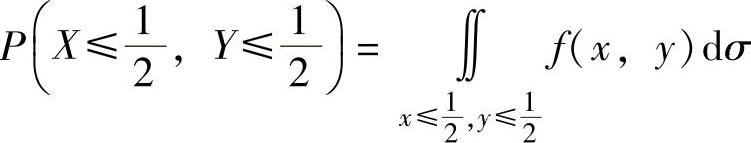
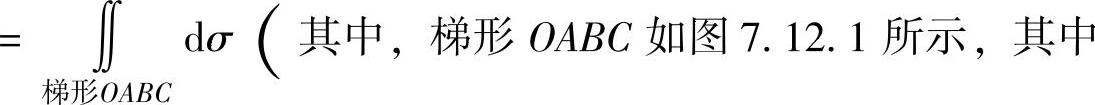
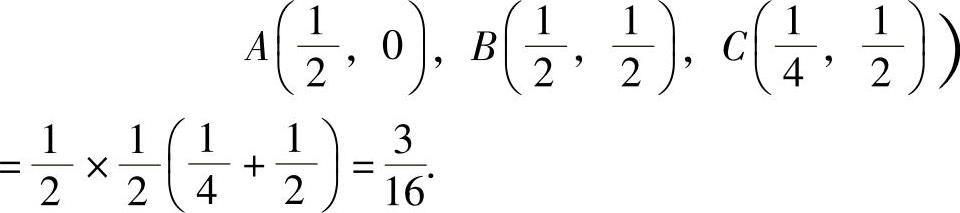
其中，978-7-111-46245-3-Part03-326.jpg978-7-111-46245-3-Part03-327.jpg978-7-111-46245-3-Part03-328.jpg

为计算978-7-111-46245-3-Part03-329.jpg，需先算出（X，Y）的关于X的边缘概率密度fX（x）：

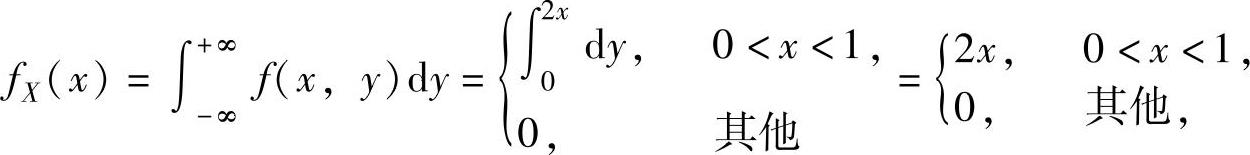
978-7-111-46245-3-Part03-330.jpg

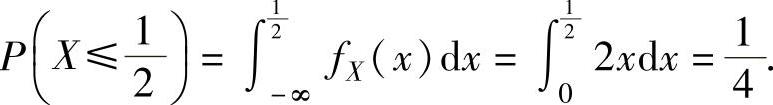
所以978-7-111-46245-3-Part03-331.jpg

将它们代入式（1）得

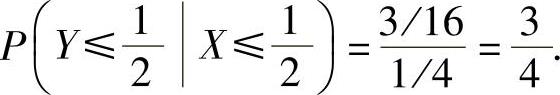
978-7-111-46245-3-Part03-332.jpg

例7.12.2 设二维随机变量（X，Y）的概率密度为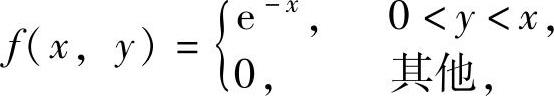978-7-111-46245-3-Part03-333.jpg求条件

概率P（X≤2Y=1）.

精解 f（x，y）在区域D={（x，y）0<y<x}（如图7.12.2阴影部分所示）上取值为e-x，在平面xOy的其他部分取值都为零.

978-7-111-46245-3-Part03-334.jpg

图 7.12.2(www.chuimin.cn)

由于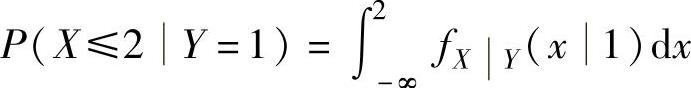978-7-111-46245-3-Part03-335.jpg，（1）

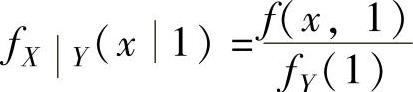其中，978-7-111-46245-3-Part03-336.jpg，（2）

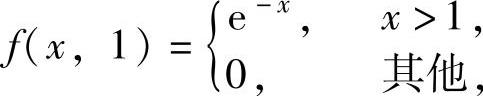
而978-7-111-46245-3-Part03-337.jpg978-7-111-46245-3-Part03-338.jpg，

将它们代入式（2）得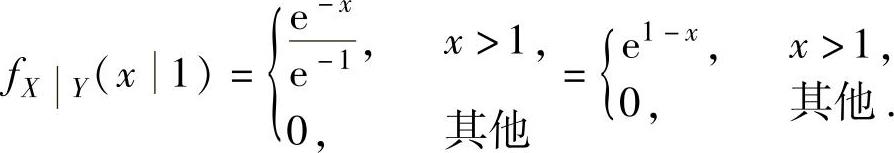978-7-111-46245-3-Part03-339.jpg

将它代入式（1）得

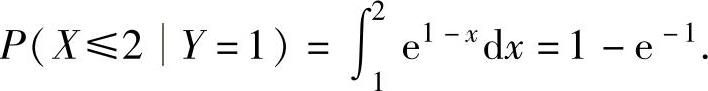
978-7-111-46245-3-Part03-340.jpg

例7.12.3 设有随机变量X，Y，且在Y=y的条件下，X的条件概率密度为

978-7-111-46245-3-Part03-341.jpg

而Y的概率密度为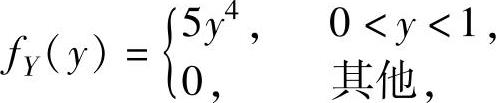978-7-111-46245-3-Part03-342.jpg求：

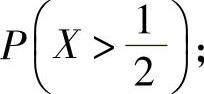
（1）概率978-7-111-46245-3-Part03-343.jpg

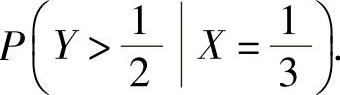
（2）条件概率978-7-111-46245-3-Part03-344.jpg

精解 （1）由于978-7-111-46245-3-Part03-345.jpg，其中fX（x）是关于X的边缘概率密度，因

此应先计算（X，Y）的概率密度f（x，y）.

由于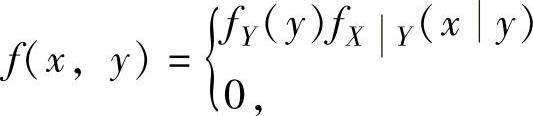978-7-111-46245-3-Part03-346.jpg，fY（y）>0，fXY（x，y）>0，

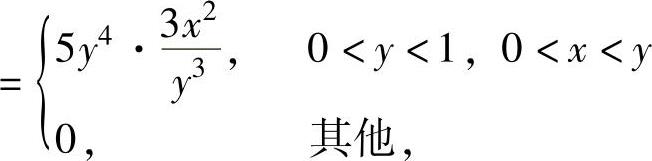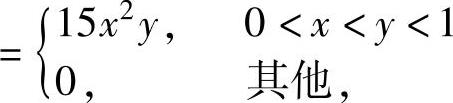
其他，978-7-111-46245-3-Part03-347.jpg，978-7-111-46245-3-Part03-348.jpg，

即f（x，y）仅在区域D={（x，y）0<x<y<1}（如图7.12.3阴影部分所示）内取非零值15x2y，

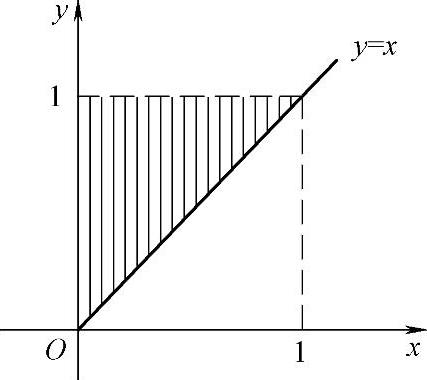
978-7-111-46245-3-Part03-349.jpg

图 7.12.3

所以978-7-111-46245-3-Part03-350.jpg，978-7-111-46245-3-Part03-351.jpg

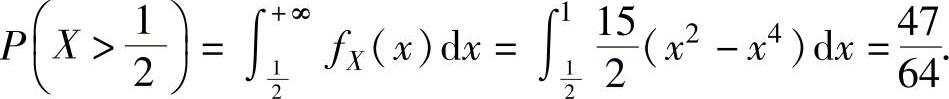
因此978-7-111-46245-3-Part03-352.jpg

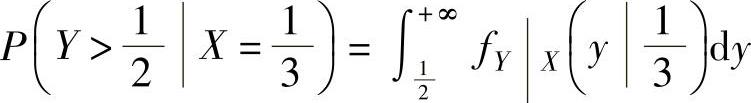（2）由于978-7-111-46245-3-Part03-353.jpg，

其中，978-7-111-46245-3-Part03-354.jpg

所以，978-7-111-46245-3-Part03-355.jpg

有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章

  • 2015考研数学基础篇-二维连续型随机变量概 2015考研数学基础篇-二维连续型随机变量概

    【主要内容】1.二维连续型随机变量及其概率密度的定义设（X，Y）是二维随机变量，如果存在非负可积函数f（x，y）（-∞

    2023-10-27

    详细阅读
  • 五连续型随机变量概率密度 五连续型随机变量概率密度

    【主要内容】1.（一维）连续型随机变量及其概率密度的概念设随机变量X，如果存在非负可积函数f（x）（-∞

    2023-10-27

    详细阅读
  • 离散型随机变量和连续型随机变量介绍 离散型随机变量和连续型随机变量介绍

    我们将这种随试验结果的不同而取不同值的变量称随机变量，记X、Y、Z等。水文上连续型随机变量是常见的，如年径流量、年降水量、年最大洪峰流量等均是连续型随机变量。......

    2023-06-21

    详细阅读
  • 连续型潮流计算的方法及应用 连续型潮流计算的方法及应用

    首先介绍纯交流系统连续型潮流计算方法的原理和步骤[1～3]。图5.1所示为连续型潮流计算法的示意图，该算法主要有4个步骤：参数化、预测、校正及步长控制。......

    2023-06-29

    详细阅读
  • 随机变量概率分布简介 随机变量概率分布简介

    对于连续型随机变量，由于其可能取值无法一一列出，而且可以证明取个别值的概率等于零。因此连续型随机变量不存在分布律。此外，连续型随机变量也可用密度函数表示其统计规律。图X3.1频率密度图和频率分布图都会成为虚线表示的光滑曲线。前者称随机变量的概率密度曲线，后者称为随机变量的概率分布曲线。......

    2023-06-21

    详细阅读
  • 2015考研数学基础篇：二维离散型随机变量及 2015考研数学基础篇：二维离散型随机变量及

    ），且取这些值对应的概率为pij（i=1，2，…），p·j=Σipij（j=1，2，…）.4.二维离散型随机变量的条件分布律设（X，Y）是二维离散型随机变量，它的分布律及边缘分布律分别为P=pij（i=1，2，…......

    2023-10-27

    详细阅读
  • 条件概率、乘法公式、全概率公式、贝叶斯公式解 条件概率、乘法公式、全概率公式、贝叶斯公式解

    ，Bn两两互不相容，且满足B1∪B2∪…∪Bn=Ω），则当P>0（i=1，2，…，n）时，对任意事件A有注 使用全概率公式解题时，可按以下原则寻找完全事件组B1，B2，…，Bn都较A先发生.贝叶斯公式：设B1，B2，…精解 先引入有关事件：A1={甲表演}，A2={乙表演}，A3={丙表演}，B={一次命中一次未命中}，则由于B与A1，A2，A3有关，且A1，A2，A3是发生于B之前的一个完全事件组，因此由全概率公式得所以......

    2023-10-27

    详细阅读
  • 水文分析计算：期望概率计算 水文分析计算：期望概率计算

    表5.20宜昌站30d洪量单位：亿m3表5.2130d洪量适线准则与总体参数的对照表由上述可知，设计洪水期望概率计算中统一采用平方和准则是适当的，以下所有参数估计均采用平方和准则确定。表5.22模拟的1000个样本频率曲线参数及设计值平均值期望概率的计算。表5.23各种频率设计洪水的期望概率由于期望概率均不大于设计值，其安全标准均超过了指定指标，故可不对设计值按期望概率进行调整。......

    2023-08-23

    详细阅读