首页理论教育标准正态分布特性及性质解析

标准正态分布特性及性质解析

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】1.标准正态分布及其分布函数的性质参数μ=0，σ=1的正态分布称为标准正态分布，记为N（0，1）.设X～Ν（0，1），则它的概率密度与分布函数分别为Φ（x）除了具有一般分布函数的性质外，还有以下性质：（1）Φ（x）是连续可导函数；（2）（3）Φ（-x）=1-Φ（x）；（4）当随机变量X～N（μ，σ2）时，概率和2.标准正态分布的上α分位数设X～N（0，1），则称满足P（X>zα）=α（

【主要内容】

1.标准正态分布及其分布函数的性质

参数_μ=0，σ=1的正态分布称为标准正态分布，记为N（0，1）.

设X～Ν（0，1），则它的概率密度与分布函数分别为

Φ（x）除了具有一般分布函数的性质外，还有以下性质：

（1）Φ（x）是连续可导函数；

（2）

（3）Φ（-x）=1-Φ（x）；

（4）当随机变量X～N（μ，σ²）时，概率和

2.标准正态分布的上α分位数

设X～N（0，1），则称满足P（X>z_α）=α（0<α<1）的实数z_α为标准正态分布的上α分位数（或上α分位数），z_α具有以下性质：对α∈（0，1）有

z_1-α=-z_α.

【典型例题】

例7.7.1 （单项选择题）设随机变量X～N（μ，4²），Y～N（μ，5²），记p₁=P（X≤μ-4），p₂=P（Y≥μ+5），则（）.

A.对任意实数μ，都有p₁=p₂

B.只对个别实数μ，有p₁=p₂

C.对任意实数μ，都有p₁<p₂

D.对任意实数μ，都有p₁>p2

精解利用ξ∈N（μ，σ²）的概率寻找正确的选项.

由于对任意实数_μ有，，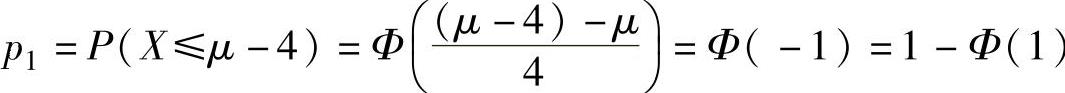

所以p₁=p_2.

因此本题选A.

例7.7.2 （单项选择题）设随机变量X～N（μ，σ²），则随σ的增大，概率P（|X-μ|<σ）（）.

A.单调增加 B.单调减少 C.保持不变 D.增减不定(www.chuimin.cn)

精解利用X～N（μ，σ²）的概率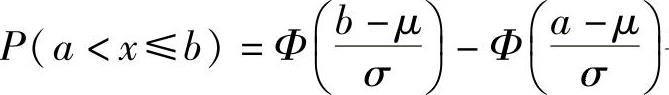寻找正确的选项.

由于

=Φ（1）-Φ（-1）（常数），所以，概率P（|X-μ|<σ）不随σ的增大而变化.

因此本题选C.

例7.7.3 （单项选择题）设X～N（0，1），u_α是N（0，1）的上α分位点（0<α<1）.如果P（|X|<x）=α，则x等于（）.

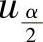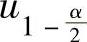A.B.C.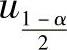D.u1-α

精解根据N（0，1）的上α分位点定义计算x，从而确定正确选项.

由P（|X|<x）=α得1-P（|X|≥x）=α，即P（|X|≥x）=1-α.从而有

于是，由N（0，1）的上α分位点定义知，x是上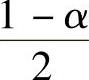分位点，即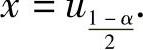

因此本题选C.

例7.7.4 服从N（220，25²）的电源电压U（单位：V）通常有三种状态：不超过220V，220～240V及超过240V.在上述三种状态下，某电子元件损坏的概率分别为0.1，0.001，0.2.求电子元件损坏的概率α（已知Φ（0.8）=0.7881）.

精解引入事件：

A={电子元件损坏}，

B₁={电源电压不超过200V}，

B₂={电源电压在220～240V}，

B₃={电源电压超过240V}，

则A与B₁，B₂，B₃有关，且B₁，B₂，B₃是先于A发生的完全事件组，所以由全概率公式得

P（A）=P（B₁）P（A|B₁）+P（B₂）P（A|B₂）+P（B₃）P（A|B₃），（1）其中，P（A|B₁）=0.1，P（A|B₂）=0.001，P（A|B₃）=0.2.下面计算P（B_i）（i=1，2，

3）.

由于U～N（220，25²），所以

将它们代入式（1）得

P（A）=0.1×0.2119+0.001×0.5762+0.2×0.2119=0.0642.