首页理论教育五连续型随机变量概率密度

五连续型随机变量概率密度

2025-09-30 理论教育版权反馈

【摘要】：【主要内容】1.（一维）连续型随机变量及其概率密度的概念设随机变量X，如果存在非负可积函数f（x）（-∞

【主要内容】

1.（一维）连续型随机变量及其概率密度的概念

设随机变量X，如果存在非负可积函数f（x）（-∞<x<+∞），使得对任意实数a，b（a<b）有，则称X是（一维）连续型随机变量，称f（x）是X的概率密度，其中f（x）有以下性质：

（1）f（x）非负可积；（2）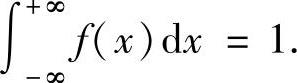

注对连续型随机变量，P（X=C）=0（C是任意实数），所以对任意实数a与b（a<b），都有

P（a<X≤b）=P（a≤X≤b）=P（a≤X<b）=P（a<X<b）.

2.常用（一维）连续型随机变量及其概率密度

（1）在区间（a，b）内服从均匀分布的随机变量

设随机变量X的概率密度为，则称X是在（a，b）内服从均匀

分布的随机变量，简称X在（a，b）内服从均匀分布，记为X～U（a，b）.

上述（a，b）也可以换成[a，b]，（a，b]或[a，b）.

注（ⅰ）当X～U（a，b）时，X落在（a，b）的任意等长子区间内的概率相等.

（ⅱ）通常，说X在（a，b）内随机取值，表明X～U（a，b）.

（2）服从指数分布的随机变量

设随机变量X的概率密度为f则称X是服从参数为λ（λ>0）的指数

分布的随机变量，简称X是服从参数为λ的指数分布，记为X～E（λ）.

（3）服从正态分布的随机变量

设随机变量X的概率密度为，则称X是服从参数为_μ，σ²（μ为实数，σ>0）的正态分布的随机变量，简称X服从参数为μ，σ²的正态分布，记为X～N（μ，σ²）.

μ=0，σ²=1时的正态分布，记为N（0，1），称为标准正态分布，当X～N（0，1）时，它的概率密度

【典型例题】

例7.5.1 （单项选择题）设f₁（x），f₂（x）都是概率密度，则（）.

A.f₁（x）+f₂（x）是概率密度

B.f₁（x）-f₂（x）是概率密度

C.对任意实数a，b，非负函数af₁（x）+bf₂（x）是概率密度

D.非负函数af₁（x）+bf₂（x）（其中，常数a，b满足a+b=1）是概率密度

精解利用概率密度的性质排除其中三个选项，即可得到正确选项.

由于f₁（x），f₂（x）都是概率密度，所以对于选项A，B，C，有未必为1，显然，这些都不符合概率密度的性质，故排除选项A，B，C.

因此本题选D.

例7.5.2 （单项选择题）设f₁（x）为服从标准正态分布的随机变量的概率密度，f₂（x）为（-1，3）内服从均匀分布的随机变量的概率密度，若

为概率密度，则a，b应满足（）.

A.2a+3b=4 B.3a+2b=4(https://www.chuimin.cn)

C.a+b=1 D.a+b=2

精解利用概率密度性质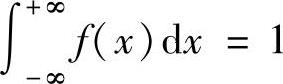判定正确的选项.

由于f（x）是概率密度，所以有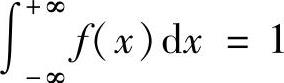，即，（1）

其中，

将它们代入式（1）得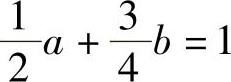，即2a+3b=4.

因此本题选A.

例7.5.3 设随机变量X的概率密度为，求：

（1）常数k的值；

（2）概率P（-1≤X<1）.

精解（1）利用概率密度性质计算k的值.

由，即，所以，从

而，

（2）

例7.5.4 设随机变量X，Y服从相同的分布，概率密度为

已知事件A={X>a}和B={Y>a}独立，且，求参数a的值，并计算概

率P（|a|<X<2|a|）.

精解首先确定a的取值范围，然后利用计算a的值，

当a≤0时，由P（A∪B）≥P（A）得，这是不可能的；

当a≥2时，由P（A∪B）=P（A）+P（B）-P（AB）=2P（A）-[P（A）]²得，

这也是不可能的，所以0<a<2，且

于是，由

得，即，所以

因此，

例7.5.5 已知某厂生产的电子元件寿命X（单位：h）服从参数为

3的指数分布，该厂规定寿命低于300h的电子元件可以要求退换.求：

（1）该厂生产的电子元件要求退换的概率p；

（2）在出售的10个电子元件中恰好有两个要求退换的概率α.

精解（1）先写出X的概率密度，然后计算概率P（X<300），即得p.X的概率密度为

所以

（2）记Y为出售的10个电子元件中要求退换的个数，则Y～B（10，p），所以