、An彼此独立,则称之为独立事件群。6.完全事件系如果多个事件A1、A2、A3、…试验的全部结果包含n个基本事件,事件A包含其中m1个基本事件,事件B包含其中m2个基本事件。定理:事件A和事件B为独立事件,则事件A与事件B同时发生的概率为各自概率的乘积,则:推理:A1、A2、…......
2023-11-17
【主要内容】
1.随机事件独立性的定义
(1)两个事件独立性的定义
设A,B是事件,如果P(AB)=P(A)P(B),则称A与B相互独立,简称独立;否则称A与B不独立.
(2)三个事件独立的定义
设A,B,C是事件,如果A,B,C中任意两个都是独立的,则称A,B,C两两独立;如果A,B,C两两独立,且满足P(ABC)=P(A)P(B)P(C),则称A,B,C相互独立,或简称独立.
2.随机事件独立的性质
设A,B,C都是事件,则
(1)当P(A)>0时,A与B独立的充分必要条件是P(B|A)=P(B).
(2)四组事件:A与B,A与 ,
,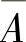 与
与 以及A与B中有一组的两个事件独立时,其余
以及A与B中有一组的两个事件独立时,其余
各组的两个事件必独立.
(3)A,B,C独立时必两两独立.
(4)当A,B,C独立时,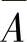 ,
,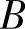 ,C;
,C; ,
, ,C;…;
,C;…;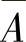 ,
,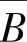 ,
,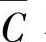 各组的三个事件也必独立.
各组的三个事件也必独立.
【典型例题】
例7.3.1 (单项选择题)将一枚硬币独立地掷两次,记事件
A1={掷第一次时,出现正面},
A2={掷第二次时,出现正面},
A3={正、反面各出现一次},
A4={正面出现两次},则( ).
A.A1,A2,A3相互独立 B.A2,A3,A4相互独立
C.A1,A2,A3两两独立 D.A2,A3,A4两两独立
精解 首先注意,如果选项A正确,则选项C必正确,这对单项选择题来说是不可能的,所以排除选项A,同样排除B.
由于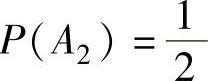 ,
, ,
,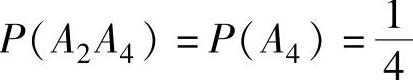 ,
,
所以P(A2A4)≠P(A2)P(A4),由此可知A2与A4不独立,即A2,A3,A4不两两独立,选项D应排除.
因此本题选C.(www.chuimin.cn)
例7.3.2 (单项选择题)设A,B是事件,它们满足0<P(A)<1,0<P(B)<1,且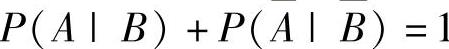 ,则( ).
,则( ).
A.A与B互不相容 B.A与B对立
C.A与B不独立 D.A与B独立
精解 由题设 得
得
P(A|B)=1-P(A|B)=P(A|B).由此可知,B发生与否不影响A发生的概率.所以A与B独立.
因此本题选D.
例7.3.3 设独立事件A,B都不发生的概率为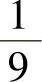 ,且A发生而B不发生的概率与B发
,且A发生而B不发生的概率与B发
生而A不发生的概率相等,求P(A).
精解 由题设知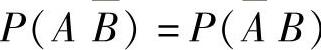 ,
,
即P(A)-P(AB)=P(B)-P(AB),所以P(A)=P(B).
此外,由A与B独立知 与
与 独立,所以由
独立,所以由 得
得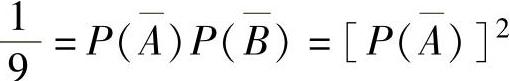 ,
,
即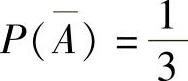 ,从而
,从而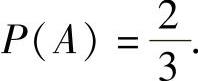
例7.3.4 甲、乙两人独立地对某一目标各射击一次,命中率分别为0.6和0.5,现已知目标被击中,求它是被乙击中的概率p.
精解 引入事件:
A={甲击中目标}, B={乙击中目标}, C={目标被击中}.
由于C=A∪B,所以概率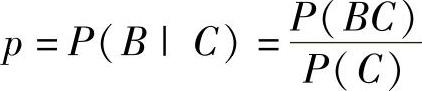 ,(1)
,(1)
其中 P(BC)=P(B(A∪B))
=P(AB∪B)=P(B)(由于AB⊂B,所以AB∪B=B)
=0.5,
P(C)=P(A∪B)=P(A)+P(B)-P(AB)
=P(A)+P(B)-P(A)P(B)(由于A与B独立)
=0.6+0.5-0.6×0.5=0.8.
将它们代入式(1)得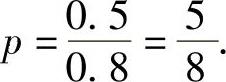
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

、An彼此独立,则称之为独立事件群。6.完全事件系如果多个事件A1、A2、A3、…试验的全部结果包含n个基本事件,事件A包含其中m1个基本事件,事件B包含其中m2个基本事件。定理:事件A和事件B为独立事件,则事件A与事件B同时发生的概率为各自概率的乘积,则:推理:A1、A2、…......
2023-11-17

将随机数作为事件出现的随机概率进行模拟工作步骤①求出模拟事件出现的概率。④从随机数表中任意指定一个随机数作为始点,一个一个的模拟。由于表7-5中分布概率、累计频率和随机概率只精确到小数点后两位数,所以获取的随机数只需两位数即可。表7-7 随机数与相应的服务时间3)将随机数加以改造,作为实际发生的事件进行模拟。目的是使模拟随机数的平均数与均方差和模拟事件的平均数与均方差相等。......
2023-07-15

)时,X与Y相互独立的充分必要条件是对任意i,j都有pij=pi··p·j当(X,Y)是二维连续型随机变量,其概率密度为f(x,y),边缘概率密度为fX和fY时,X与Y相互独立的充分必要条件是f(x,y)=fXfY在xOy平面上几乎处处成立.注 (ⅰ)设随机变量X与Y相互独立,g,h是连续函数,则随机变量Z1=g与Z2=h也相互独立.(ⅱ)多个随机变量的独立性也可类似定义.如果对任意实数x1,x2,…,Fn分别是随机变量X1,X2,…......
2023-10-27

现实生活中,很多变量的变化是连续不断的,比如气温的变化、植物的生长、物体受热时面积的变化等,都是连续的变化.这种现象在数学上用函数的连续性来反映和研究.一、连续函数的概念定义1.21 在函数y=f(x)的定义域中,设自变量x由x0变到x1,差Δx=x1-x0叫做自变量x的增量(改变量),相应的函数值的差Δy=f(x1)-f(x0)=f(x0+Δx)-f(x0)叫做函数y=f(x)的增量(见图1-1......
2023-11-22

为了考虑PBX 参数的非均匀性,引入威布尔概率分布,实现各单元材料属性随机力学参数赋值。为了清晰地描述PBX 材料破坏损伤过程,对弹性模量、泊松比、拉伸强度、断裂能等参数进行威布尔概率统计分析,在巴西圆盘实验的有限元计算中得到应用。图4-11威布尔随机数的分布函数图4-12巴西实验有限元模型......
2023-06-27

在第1章我们简单介绍了算法的概念,并指出:软件的主体是程序,程序的核心是算法。算法既是人类之间交流智能的工具,也是人和机器之间交流智能的工具。算法的可终止性是指算法应能在有限的操作步骤后结束。我们仍以第1章给出的求解两个整数的最大公约数问题的算法为例,来讨论算法的定义问题。所以,上述方法不是一个算法。计算机求解任何问题,必须在一个有限的时间段内得到处理结果,算法的可终止性保证了这一点。......
2023-11-18

【主要内容】设二元函数z=f(x,y)在点(x0,y0)的某个邻域内有定义.如果它在点(x0,y0)处的全增量Δz=f(x0+Δx,y0+Δy)-f(x0,y0)可以表示为Δz=AΔx+BΔy+o(ρ)(其中A和B不依赖于Δx,Δy,o(ρ)是比ρ=高阶的无穷小),则称z=f(x,y)在点(x0,y0)处可微,称AΔx+BΔy为z=f(x,y)在点(x0,y0)处的全微分,记为,即注 (ⅰ)二元函......
2023-10-27

田宅宫和兄弟宫是财库,但性质不同。田宅宫纳音代表公尺数,如木三局表示宅外300米有学校。)若田宅宫无主星表示其人的住宅附近有空地。尤其是火星、在火灾事件中,火星在田宅宫的出现率最高,可以说火星是最正宗的火灾星,其次是廉贞。又若田宅宫在寅宫,且该宫的天干为丙,则暴发火灾的几率最高。有时仅田宅宫有火星、廉贞、禄存,而夫妻宫没有化忌,并不表示一定会发生火灾。......
2023-10-29
相关推荐