首页 理论教育条件概率、乘法公式、全概率公式、贝叶斯公式解析

条件概率、乘法公式、全概率公式、贝叶斯公式解析

2023-10-27 理论教育 版权反馈
【摘要】：，Bn两两互不相容，且满足B1∪B2∪…∪Bn=Ω），则当P>0（i=1，2，…，n）时，对任意事件A有注 使用全概率公式解题时，可按以下原则寻找完全事件组B1，B2，…，Bn都较A先发生.贝叶斯公式：设B1，B2，…精解 先引入有关事件：A1={甲表演}，A2={乙表演}，A3={丙表演}，B={一次命中一次未命中}，则由于B与A1，A2，A3有关，且A1，A2，A3是发生于B之前的一个完全事件组，因此由全概率公式得所以

【主要内容】

1.条件概率的定义

设A，B是事件，P（A）>0，则称A发生条件下B发生的概率为条件概率，记为P（B|A），且定义978-7-111-46245-3-Part03-16.jpg

注 条件概率也是概率，所以它也具有概率的所有性质，例如

P（B|A）=1-P（B|A），

P（B1∪B2|A）=P（B1|A）+P（B2|A）-P（B1B2|A），

P（B1-B2|A）=P（B1|A）-P（B1B2|A）.

2.乘法公式

设A，B是事件，则

注 （ⅰ）当P（A），P（B）都大于零时，欲用乘法公式解题时，总是将A，B中先发生的事件作为条件来考虑条件概率，例如，当A先发生时，总是使用P（AB）=P（A）P（B|A）.

（ⅱ）当P（AB）>0时有P（ABC）=P（A）P（B|A）P（C|AB）.

3.全概率公式与贝叶斯公式

全概率公式：

设B1，B2，…，Bn是一个完全事件组（即B1，B2，…，Bn两两互不相容，且满足B1∪B2∪…∪Bn=Ω），则当P（Bi）>0（i=1，2，…，n）时，对任意事件A有

注 使用全概率公式解题时，可按以下原则寻找完全事件组B1，B2，…，Bn：

（ⅰ）B1，B2，…，Bn与A有关；

（ⅱ）B1，B2，…，Bn都较A先发生.

贝叶斯公式：

设B1，B2，…，Bn是一个完全事件组，且P（Bi）>0（i=1，2，…，n），则当P（A）>0时，

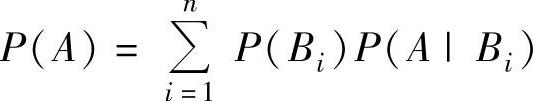注 实际上，贝叶斯公式是条件概率与全概率公式的直接推论，因此计算条件概率P（Bi|A）时，不必直接使用贝叶斯公式，而先用条件概率计算公式978-7-111-46245-3-Part03-20.jpg，然后再用全概率公式计算P（A）（P（BiA）是978-7-111-46245-3-Part03-21.jpg的右边第i项）.

【典型例题】

例7.2.1 （单项选择题）设事件A，B满足0<P（A）<1，0<P（B）<1，P（A|B）≥978-7-111-46245-3-Part03-22.jpg，则有（ ）.

A.978-7-111-46245-3-Part03-23.jpgB.978-7-111-46245-3-Part03-24.jpg

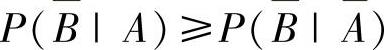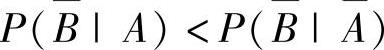
C.978-7-111-46245-3-Part03-25.jpgD.978-7-111-46245-3-Part03-26.jpg

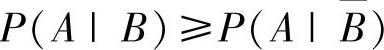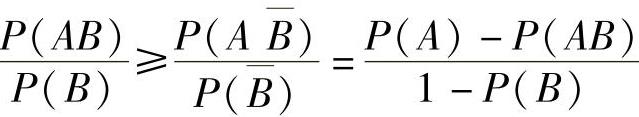精解 从题设P（A|B）≥P（A|B）出发进行推理.由978-7-111-46245-3-Part03-27.jpg得978-7-111-46245-3-Part03-28.jpg，即P（AB）-P（AB）P（B）≥P（A）P（B）-P（AB）P（B），化简后得

P（AB）≥P（A）P（B）.由此得到P（A）P（B|A）≥P（A）P（B），

于是有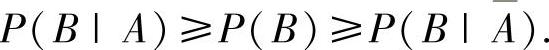978-7-111-46245-3-Part03-29.jpg

因此本题选A.

例7.2.2 在10件产品中有4件一等品，6件二等品.现从中任取两次，每次取一件取后不放回.已知其中至少有一件是一等品，求两件都是一等品的概率.

精解 引入随机事件

A={先取出的一件产品为一等品}，

B={后取出的一件产品为一等品}，则欲求概率为条件概率P（AB|A∪B）.由条件概率计算公式得978-7-111-46245-3-Part03-30.jpg，（1）

其中，978-7-111-46245-3-Part03-31.jpg，（2）

将式（2）、式（3）代入式（1）得

例7.2.3 袋内有7个球，其中4个红球，3个白球.现不放回地取球，每次取1个.

（1）求第2次取球才取到白球的概率p1；(www.chuimin.cn)

（2）求第2次取球取到的是白球的概率p2；

（3）求第1，2次取球取到的是同色球的概率p3.

精解 引入随机事件Ai={第i次取球取到的是白球}（i=1，2）.

（1）{第2次取球才取到白球}={第1次未取到白球而第2次取球取到白球978-7-111-46245-3-Part03-34.jpg

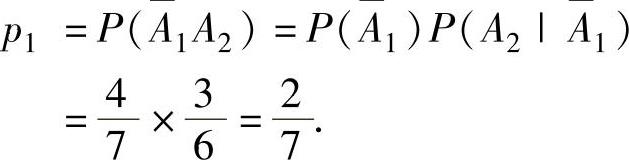
所以，978-7-111-46245-3-Part03-35.jpg

（2）p2=P（第2次取球取到的是白球）=P（A2）.

由于A2与A1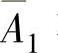，978-7-111-46245-3-Part03-36.jpg有关，显然A1，978-7-111-46245-3-Part03-37.jpg都发生于A2之前，且是一个完全事件组，所以，

由全概率公式得

（3）{第1，2次取球取到的是同色球}

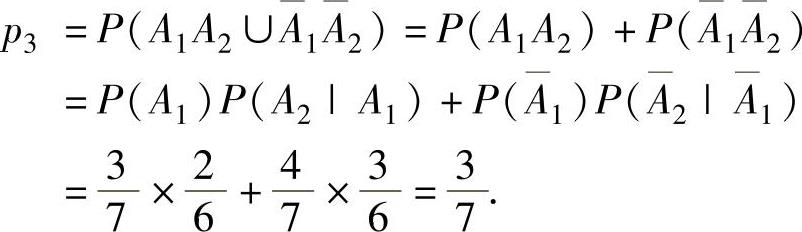
={第1，2次取球取到的都是白球或都是红球}978-7-111-46245-3-Part03-39.jpg（其中A1A2，A1A2互不相容），所以，978-7-111-46245-3-Part03-40.jpg

例7.2.4 两位男士和一位女士坐在候诊室W1内，一位男士和两位女士坐在候诊室W2内，医生从W2随机叫出一人之前，有一个人从W1到W2去候诊.已知被叫出的人恰好是男士，求换候诊室的人也是男士的概率.

精解 先引入事件

A={换候诊室的人是男士}，

B={被叫出的人是男士}，则欲求的概率是条件概率P（A|B）.由条件概率计算公式得

由于B与A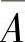，978-7-111-46245-3-Part03-42.jpg有关，显然A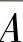，978-7-111-46245-3-Part03-43.jpg都发生于B之前，且是一个完全事件组，所以由全概

率公式得

所以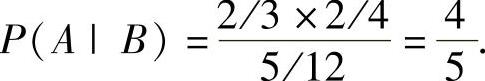，978-7-111-46245-3-Part03-45.jpg

例7.2.5 玻璃杯成箱出售，每箱20个.设每箱有0，1，2个残次品的概率分别为0.8，0.1，0.1.一位顾客欲购一箱玻璃杯，在购买时，售货员随意取出一箱，而顾客随机地察看其中4个玻璃杯，若无残次品，则买下这箱玻璃杯，否则退回.

（1）求顾客买下该箱玻璃杯的概率α；

（2）已知顾客买下该箱玻璃杯，求该箱玻璃杯中残次品数为零的概率β.

精解 引入有关的事件：

A={顾客买下该箱玻璃杯}={顾客察看的4个玻璃杯中无残次品}，

Bi={该箱玻璃杯的残次品数为i}（i=0，1，2）.

（1）由于A={顾客察看的4个玻璃杯中无残次品}，所以A与B0，B1，B2有关，且B0，B1，B2是发生于A之前的一个完全事件组.因此由全概率公式得

α=P（A）=P（B0）P（A|B0）+P（B1）P（A|B1）+P（B2）P（A|B2），（1）

其中，978-7-111-46245-3-Part03-46.jpg，978-7-111-46245-3-Part03-47.jpg，

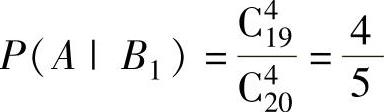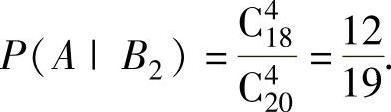
P（A|B0）=1，978-7-111-46245-3-Part03-48.jpg，978-7-111-46245-3-Part03-49.jpg

将它们代入式（1）得

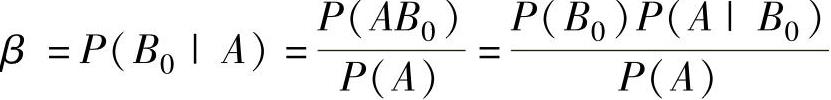
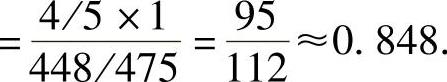
（2）978-7-111-46245-3-Part03-51.jpg978-7-111-46245-3-Part03-52.jpg

例7.2.6 甲、乙、丙三人进行一次射击比赛，赛前发现只带两发子弹，因此将比赛改为一人进行射击表演，并且由抽签确定表演者，设每次射击的命中率甲为0.9，乙为0.5，丙为0.2，且已知射击结果为一次命中一次未命中，问表演者为甲、乙、丙的概率各为多少？

精解 先引入有关事件：

A1={甲表演}，A2={乙表演}，A3={丙表演}，

B={一次命中一次未命中}，则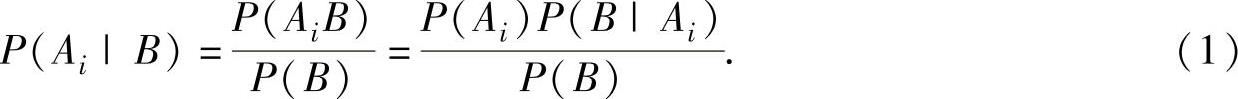978-7-111-46245-3-Part03-53.jpg

由于B与A1，A2，A3有关，且A1，A2，A3是发生于B之前的一个完全事件组，因此由全概率公式得

所以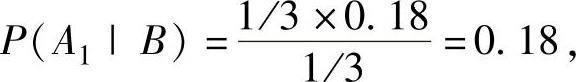978-7-111-46245-3-Part03-55.jpg978-7-111-46245-3-Part03-56.jpg

有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章

  • 图乘法的使用条件和公式详解 图乘法的使用条件和公式详解

    对于由多个弯曲刚度EI为常数的杆段组成的结构，用图乘法计算位移的公式为显然，图乘法是将积分运算问题简化为求图形的面积、形心和竖标的问题。需要说明的是，用图乘法计算位移时，梁和刚架的杆件必须满足以下条件：杆段的弯曲刚度EI为常数。下面给出了图乘运算中几种常见图形的面积及其形心位置，如图13-14所示。......

    2023-06-16

    详细阅读
  • 公式比较：与其他公式对比 公式比较：与其他公式对比

    下面就基于通用水流功率概念建立的输沙能力公式与常用的Engelund-Hansen公式、Ackers-White公式、Yang公式以及Toffaleti公式进行比较。Engelund-Hansen 公式是公认的比较可靠的公式之一，在实际中得到了广泛应用。考虑到Toffaleti的输沙率公式主要是依据大河流的资料建立的，本节的比较也包括了该式在内。对于414组大河流的资料，公式和Toffaleti方法得到的计算与实测含沙量之间的平均偏差比R分别为1.14和1.19，Engelund-Hansen公式和Ackers-White公式的平均偏差比R分别为2.21和1.65。......

    2023-06-22

    详细阅读
  • 数学海洋：乘法公式的演化 数学海洋：乘法公式的演化

    《几何原本》中的乘法公式资料表明,早在公元前1700 年左右,古巴比伦人已会用简单的乘法公式,当然他们是用文字表述。在欧几里得《几何原本》第二卷中,给出一系列乘法公式的文字叙述和逻辑证明,因未引进数学符号,叙述显得有些啰嗦。图3.16.4古法七乘方图图3.16.5帕斯卡近年来,国外一些学者也逐渐承认这项成果的优先权属于中国,有些文献已称之为“中国三角形”。......

    2023-11-23

    详细阅读
  • 大数据挖掘技术在医药领域中的贝叶斯公式应用 大数据挖掘技术在医药领域中的贝叶斯公式应用

    ，n），则3.贝叶斯定理贝叶斯，在《An Essay towards solving a Problem in the Doctrine of Chances》中给出了贝叶斯定理。其基本求解公式：贝叶斯公式：P（B|A）是根据A判断其属于类别B的概率，称为后验概率。......

    2023-11-08

    详细阅读
  • 高等数学中的泰勒公式及麦克劳林公式 高等数学中的泰勒公式及麦克劳林公式

    =f=e0=1，f（n+1）（θx）=eθx.故f=ex的n阶麦克劳林公式为例2 求f=sinx的带有拉格朗日型余项的n阶麦克劳林公式.解 ，所以f=0，f′=1，f″=0，f=-1，f=0，…从而其中，例3 求.解 ，，所以原式.几个常用函数的麦克劳林公式：由以上带有佩亚诺型余项的麦克劳林公式，易得相应的带有拉格朗日型余项的麦克劳林公式，读者可自行写出.......

    2023-11-22

    详细阅读
  • 大河流输沙能力公式 大河流输沙能力公式

    Einstein 认为，水流的输沙能力与水流克服沙粒阻力所要求的能坡J′有关，而不是总能坡J。式表示的关系式与Velikanov、张瑞瑾、窦国仁分别提出的式 (2-2)、式(2-4)、式(2-5)表示输沙能力关系的形式基本相同。因此，在大河流的输沙能力计算公式中，选择合适的阻力公式，将比降表示为速度和水深的函数，是一种较为有效的处理办法。根据表2-1给出的414组大河流输沙资料点绘了Ct与Ψ 的关系，见图2-4。......

    2023-06-22

    详细阅读
  • 复积分计算公式及条件 复积分计算公式及条件

    下面讨论积分式(3.1.1)在什么条件下存在.函数f(z)=u(x,y)+iv(x,y)在D内处处连续,则u(x,y)及v(x,y)均为D内的连续函数.设ζk =ξk+iηk,由于因此由于u,v都是连续函数,根据线积分的存在定理可知,当弧段长度的最大值趋于零时,不论对C的分法如何,点(ξk,ηk) 的取法如何,上式右端的两个和式的极限都是存在的.因此有为便于记忆,公式(3.1.2)在形式上可以看作......

    2023-10-30

    详细阅读
  • 推导推移质公式 推导推移质公式

    推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。Einstein 经过推导得出在单位面积上将有重量为的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。图1-2修正的Einstein公式与实测资料的对比图1-2修正的Einstein公式与实测资料的对比......

    2023-06-22

    详细阅读