2015考研数学基础篇：随机事件及概率概念

2023-10-27 理论教育版权反馈

【摘要】：都是随机事件，如果其中任意两个都是互不相容的，则称A1，A2，…

【主要内容】

1.随机事件

随机试验E的所有可能结果的集合，称为样本空间，记为Ω，Ω的每个元素称为样本点，Ω的每个子集称为随机事件（简称事件），用A，B，A_i等表示，特别地，称其中的单点集为基本事件，称空集为不可能事件，记为，称Ω为必然事件.

（1）随机事件间的关系

包含：设A，B是事件，如果A发生必导致B发生，则称A包含于B（或B包含A），记为A⊂B（或B⊃A）.

相等：设A，B是事件，如果A⊂B且B⊂A，则称A，B相等，记为A=B.

互不相容：设A，B是事件，如果A，B不同时发生，则称A，B互不相容（或互斥）.

两两互不相容：设A₁，A₂，…，A_n，…都是随机事件，如果其中任意两个都是互不相容的，则称A₁，A₂，…，A_n，…两两互不相容.

对立：设A，B是随机事件，如果A与B有且仅有一个发生，则称A与B对立，此时也称B为A的逆事件，记为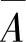，即，也称A是B的逆事件，记为，即

独立：（见本章三）.

（2）随机事件的运算

和运算：设A，B是事件，则称A∪B是A与B的和事件，它是当且仅当A，B中至少有一个发生时才发生的事件.由事件A，B产生事件A∪B的运算称为和运算.

和运算可以推广到n个事件情形和无限可列个事件情形.

积运算：设A，B是事件，则称A∩B（简记为AB）是A与B的积事件，它是当且仅当A与B同时发生时才发生的事件.由事件A，B产生事件AB的运算称为积运算.

积运算可以推广到n个事件情形和无限可列个事件情形.

差运算：设A，B是事件，则称A-B是A与B的差事件，它是当且仅当A发生而B不发生时才发生的事件.由事件A，B产生A-B的运算称为差运算.

上述运算有以下性质：设A，B，C都是事件，则

A∪B=B∪A，AB=BA；

（A∪B）∪C=A∪（B∪C），（AB）C=A（BC）；

A∪（BC）=（A∪B）（A∪C），A（B∪C）=AB∪AC；

A∪A=A，AA=A；

A∪Ω=Ω，A∪=A；

AΩ=A，A=；

2.随机事件概率的定义

设随机试验E的样本空间为Ω，如果Ω的任一事件A都有唯一的满足下列条件的实数P（A）与之对应，则称P（A）为A的概率：

（1）P（A）≥0；

（2）P（Ω）=1；

（3）对两两互不相容事件A₁，A₂，…，A_n，…有

3.随机事件概率的计算公式：设A，B，C是事件，则有以下的概率计算公式：

（1）逆事件概率公式（简称逆概公式）

（2）加法公式

P（A∪B）=P（A）+P（B）-P（AB），特别地，当A与B互不相容时有P（A∪B）=P（A）+P（B）.

P（A∪B∪C）=P（A）+P（B）+P（C）-P（AB）-P（AC）-P（BC）+P（ABC），特别地，当A，B，C两两互不相容时，P（A∪B∪C）=P（A）+P（B）+P（C）.

（3）减法公式

P（A-B）=P（A）-P（AB），特别地，当A⊃B时，P（A-B）=P（A）-P（B）.(www.chuimin.cn)

（4）乘法公式（见本章二）

4.古典概型与几何概型的随机事件的概率（即古典型概率与几何型概率）

（1）古典型概率的定义

如果随机试验E的样本空间Ω只有有限个基本事件，且每个基本事件发生的可能性相同，则称这样的随机试验E为古典概型.设A是E的事件，则定义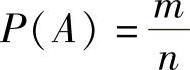（古典型概率），其中，n是Ω的基本事件个数，m是A包含的基本事件个数.

（2）几何型概率的定义

如果随机试验E是从某一线段（或平面、空间中有界区域）Ω上任取一点，并且所取的点位于Ω中任意两个长度（或面积、体积）相等的子区间（或子区域）内的可能性相同，则这样的E称为几何概型，记A为所取点位于Ω中任意子区间（或子区域）G内这一事件，则定义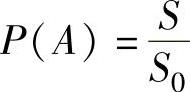（几何型概率），其中，S₀，S分别是Ω与G的长度（或面积、体积）.

【典型例题】

例7.1.1 （单项选择题）记随机事件A={甲种产品畅销而乙种产品滞销}，则A为（）.

A.{甲种产品滞销而乙种产品畅销}

B.{甲、乙两种产品都畅销}

C.{甲种产品滞销}

D.{甲种产品滞销或乙种产品畅销}

精解记A₁={甲种产品畅销}，A₂={乙种产品滞销}，则

A=A₁A2.于是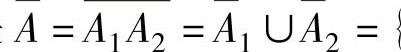甲种产品滞销或乙种产品畅销}.

因此本题选D.

例7.1.2 （单项选择题）设只有当事件A与B同时发生时，事件C才发生，则（）.

A.P（C）≤P（A）+P（B）-1 B.P（C）≥P（A）+P（B）-1

C.P（C）=P（AB） D.P（C）=P（A∪B）

精解由于事件A与B同时发生时事件C发生，所以AB⊂C.由此得到P（C）≥P（AB）=P（A）+P（B）-P（AB）≥P（A）+P（B）-1.因此本题选B.

例7.1.3 设A，B是事件，且P（A）=0.6，P（B-A）=0.3，求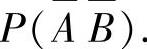

精解用概率计算公式计算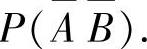

P（AB）=1-P（A∪B）=1-[P（A）+P（B）-P（AB）]

=1-P（A）-[P（B）-P（AB）]

=1-P（A）-P（B-A）（这里利用P（B-A）=P（B）-P（AB））

=1-0.6-0.3=0.1.

例7.1.4 从5双不同号码的鞋子中任取4只，求4只鞋子中至少有两只配成一双的概率.

精解先引入有关的事件：

A={4只鞋子中至少有两只配成一双}，

A₁={4只鞋子中恰有两只配成一双}，

A₂={4只鞋子中恰好配成两双}，由于A₁，A₂的概率较A的概率易于计算，所以用A₁，A₂表示A后再用概率计算公式计算P（A）.

由于A=A₁∪A₂，且A₁与A₂互不相容，所以

P（A）=P（A₁）+P（A₂）（1）其中P（A₁），P（A₂）都是古典型概率.由于A₁表示4只鞋子中恰有两只成双，而其余两只不成双，前者有C₅¹种不同取法，而后者可以从剩下的四双鞋子中任取两只左脚的或两只右脚的，也可以取一只左脚的，另一只是与此不成双的右脚的，所以有C₂¹C₄²+C₄¹C₃¹种不同取法.从而

A₂表示4只鞋子恰好配成两双，即从5双鞋子中任取两双，所以共有C²₅种不同取法，因此，

将式（2）、式（3）代入式（1）得

2015考研数学基础篇：随机事件及概率概念

相关推荐