【摘要】:,xn)为正定二次型,称实对称矩阵A为正定矩阵.2.二次型为正定二次型的充分必要条件设二次型f(x1,x2,…
【主要内容】
1.正定二次型与正定矩阵的定义
设二次型f(x1,x2,…,xn)=xTAx,其中,A是n阶实对称矩阵,x=(x1,x2,…,xn)T.如果对于任意x0=(x01,x02,…,x0n)≠0,都有f(x1,x2,…,xn)>0,则称f(x1,x2,…,xn)为正定二次型,称实对称矩阵A为正定矩阵.
2.二次型为正定二次型的充分必要条件
设二次型f(x1,x2,…,xn)=xTAx,其中,A为n阶实对称矩阵,x=(x1,x2,…,xn)T,则f为正定二次型的充分必要条件常见的有以下5种:
(1)f的正惯性指数为n.
(2)f的矩阵A的特征值全都为正值.正定二次
(3)f的矩阵A合同于En.
(4)f的各阶顺序主子式全都大于零.
(5)存在n阶可逆矩阵C,使得f的矩阵A=CTC.
3.实对称矩阵为正定矩阵的充分必要条件
设A是n阶实对称矩阵,则A为正定矩阵的充分必要条件常见的有以下5种:
(1)二次型f(x1,x2,…,xn)=xTAx是正定二次型.
(2)A的特征值都为正值.
(3)A≃En或A≃B(正定矩阵).
(4)A的各阶顺序主子式都大于零.
(5)存在n阶可逆矩阵C,使得A=CTC.
注 正定矩阵还有以下性质:
(ⅰ)当A,B都为正定矩阵时,A+B为正定矩阵;
(ⅱ)当A为正定矩阵,常数k>0时,kA为正定矩阵;
(ⅲ)当A是正定矩阵时,A-1是正定矩阵.
(ⅳ)当A是正定矩阵时,A∗是正定矩阵.
(ⅴ)当A1,A2都是正定矩阵时,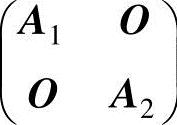 是正定矩阵.
是正定矩阵.
【典型例题】
例6.11.1(单项选择题) 设n阶矩阵A既是正交矩阵,又是正定矩阵,则A为( ).
A.-En B.En C.2En D.2A
精解 由题设知A是正交且对称矩阵,所以
En=ATA=A2,即(En-A)(En+A)=On.(1)(www.chuimin.cn)
由A是正定矩阵知,-1不是A的特征值,因此En+A可逆,从而由式(1)得En-A=On,即A=En.
因此本题选B.
例6.11.2 设A为三阶实对称矩阵,且满足A2+2A=O3及r(A)=2.
(1)求A的全部特征值;
(2)问k为何值时,矩阵kE3+A为正定矩阵.
精解 (1)设A的特征值为λ,则由A2+2A=O3知λ满足
λ2+2λ=0,即λ=0,-2.
此外,由A是实对称矩阵知,它必相似于对角矩阵Λ,于是由r(Λ)=r(A)=2知Λ=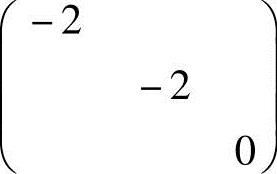 ,即A的全部特征值为-2,-2,0.
,即A的全部特征值为-2,-2,0.
由于kE3+A的全部特征值为k-2,k-2,k,于是当k>2时,这三个特征值全大于零,此时kE3+A是正定矩阵.
例6.11.3 设二次型f(x1,x2,x3)=λ(x21+x22+x23)+2x1x2+2x1x3-2x2x3,问λ取何值时,f(x1,x2,x3)是正定的.
精解 f(x1,x2,x3)的矩阵为
它的各阶顺序主子式为
于是当λ满足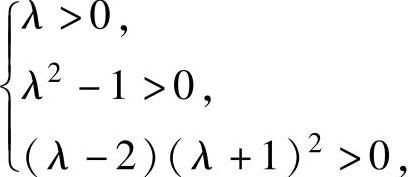 即λ>2时,f(x1,x2,x3)是正定的.
即λ>2时,f(x1,x2,x3)是正定的.
例6.11.4 设A是m×n矩阵,且B=λEn+ATA.证明:对任意正数λ,B都是正定矩阵.
精解 先证明B是实对称矩阵,然后用定义证明B是正定的.
由于BT=(λEn+ATA)T=(λEn)T+(ATA)T=λEn+ATA=B,所以B是实对称矩阵.
记f(x1,x2,…,xn)=xTBx(其中,x=(x1,x2,…,xn)T),则对于任意x0=(x01,x02,…,x0n)T≠0有
f(x01,x02,…,x0n)=x0TBx0=x0T(λEn+ATA)x0
=λx0Tx0+x0TATAx0>(Ax0)T(Ax0)(由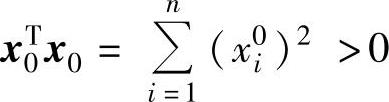 ,λ>0知λx0Tx0>0)
,λ>0知λx0Tx0>0)
>0(由x0≠0,A可逆知Ax0≠0,从而(Ax0)T(Ax0)>0).因此f(x1,x2,…,xn)是正定二次型,从而对任意正数λ,B=λEn+ATA是正定的.
例6.11.5 已知A,B都是n阶正定矩阵,证明:AB是正定矩阵的充分必要条件是AB=BA.
精解 必要性,设AB是正定矩阵,则AB必是实对称矩阵,所以有
AB=(AB)T=BTAT=BA(由A,B是正定矩阵知AT=A,BT=B).
充分性.设AB=BA,则与证明必要性同样可证(AB)T=AB,即AB是实对称矩阵,由于A,B是正定矩阵,所以存在n阶可逆矩阵R和S,使得
A=RTR,B=STS.于是,(RT)-1(AB)RT=(RT)-1RTRSTSRT=RSTSRT=(SRT)T(SRT).(1)
由于 SRT是可逆矩阵,所以(SRT)T(SRT)是正定矩阵.因此由式(1)知,实对称矩阵AB与正定矩阵(SRT)T(SRT)相似,从而AB是正定矩阵.

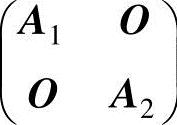 是正定矩阵
是正定矩阵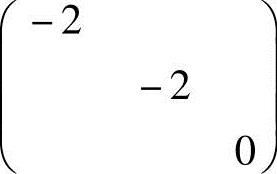 ,即A的全部特征值为-2,-2,0
,即A的全部特征值为-2,-2,0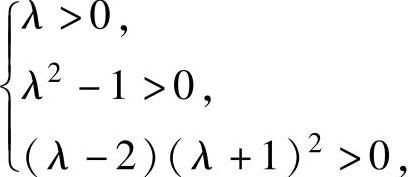 即
即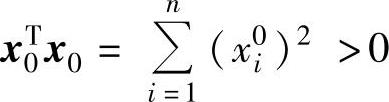 ,
,





相关推荐