二次型化规范形的方法及步骤

2023-10-27 理论教育版权反馈

【摘要】：，xn）T）具有相同的规范形.2.二次型化规范形的方法设二次型f（x1，x2，…，xn）T，A是n阶实对称矩阵），可按以下步骤将它化为规范形：将f（x1，x2，…

【主要内容】

1.规范形的概念

如果二次型是标准形，且其中系数只取1，-1，0三个数，则称这种二次型为规范形.

任意二次型f（x₁，x₂，…，x_n）=x^TAx（x=（x₁，x₂，…，x_n）^T）都可经变量之间的可逆线性变换化为规范形，而且规范形是唯一的，即系数为1的项数p（称为正惯性指数）与系数为-1的项数q（称为负惯性指数）是由原二次型唯一确定的（惯性定理）.

显然，p+q=r（A），且p，q，n-p-q分别为A的正、负、零特征值的个数.

以下结论是有用的：

两个n阶实对称矩阵A，B相似的充分必要条件是它们具有相同的特征值及重数；

两个n阶实对称矩阵A，B合同的充分必要条件是二次型x^TAx与x^TBx（其中，x=（x₁，x₂，…，xn）T）具有相同的规范形.

2.二次型化规范形的方法

设二次型f（x₁，x₂，…，x_n）=x^TAx（其中，x=（x₁，x₂，…，x_n）^T，A是n阶实对称矩阵），可按以下步骤将它化为规范形：

（1）将f（x₁，x₂，…，x_n）化为标准形，即

f（x₁，x₂，…，x_n）=d1y²1+d₂y²2+…+d_ny²_n；

（2）令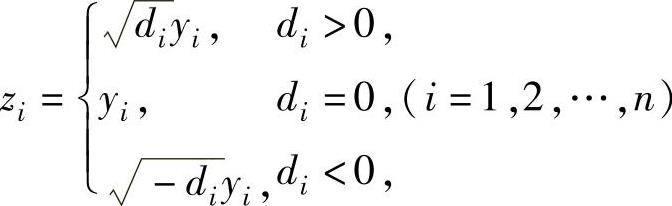将f（x₁，x₂，…，x_n）=d₁y²1+d₂y²₂+…+d_ny²n

化为规范形，即

f（x₁，x₂，…，x_n）=ε1z²1+ε2z²2+…+ε_nz²_n，

其中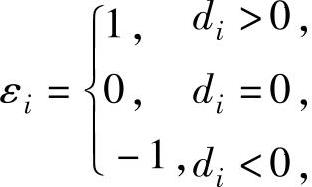，（i=1，2，…，n）.【典型例题】

例6.10.1 （单项选择题）设二阶矩阵，则与A合同的矩阵为（）.

精解

由于x^TAx=x²₁+4x₁x₂+x²₂=（x²₁+4x₁x₂+4x²₂）-3x²2=（x₁+2x₂）2-3x²₂=y²₁-y²₂（其中，，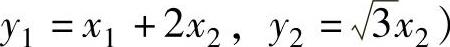

所以由选项A，B，C对应的二次型分别为

知它们都不可能与x^TAx具有相同的规范形，即选项A，B，C都不能选.

因此本题选D.(www.chuimin.cn)

例6.10.2 设二次型f（x₁，x₂，x₃）=（1-a）x²₁+（1-a）x²₂+2x²₃+2（1+a）x₁x₂的秩为2，求参数a，并用可逆线性变换x=Py（其中x=（x₁，x₂，x₃）^T，y=（y₁，y₂，y₃）^T）将f（x₁，x₂，x3）化为规范形（要求写出矩阵P）.

精解先根据f（x₁，x₂，x₃）的秩为2确定a的值，并用配方法将f（x₁，x₂，x₃）化为标准形，然后化为规范形及写出P.

记f（x₁，x₂，x₃）的矩阵为A，则

于是，由f（x₁，x₂，x₃）的秩为2，即r（A）=2得A=2[（1-a）2-（1+a）2]=0，所以a=0.

因此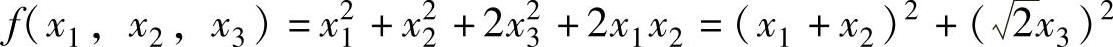=y²₁+y²₃（规范形），

其中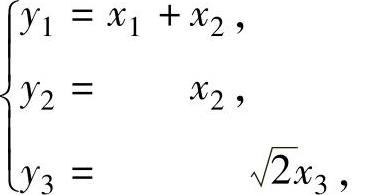即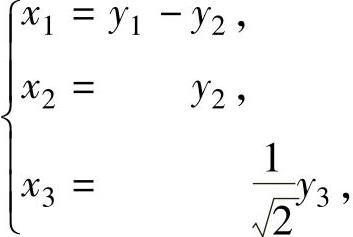或者x=Py，其中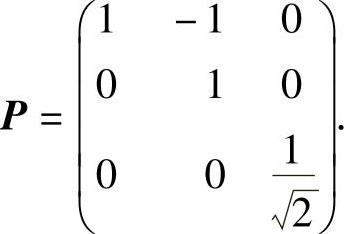

例6.10.3 设二次型f（x₁，x₂，x₃）=ax²₁+ax²₂+（a-1）x²₃+2x₁x₃-2x₂x₃的规范形为y²_1+y22，求a.

精解从f的矩阵有两个正特征值与一个零特征值入手计算a的

值.

由于f的规范形为y²₁+y²₂，所以A的正惯性指数p=2，负惯性指数q=0.因此，A的三个特征值中有两个为正的，一个为零.

由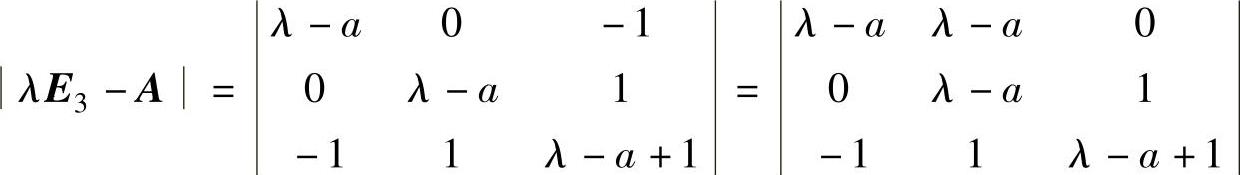

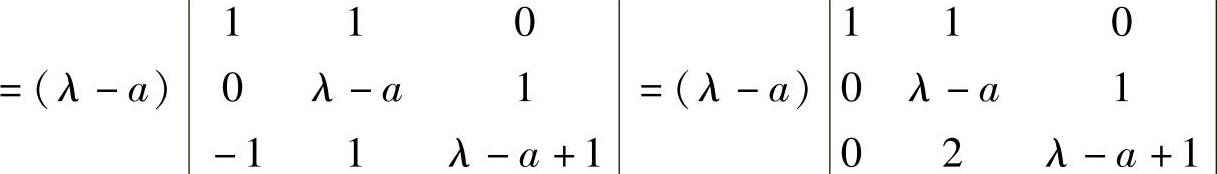
=（λ-a）[（λ-a）（λ-a+1）-2]

=（λ-a）（λ-a+2）（λ-a-1）知A有特征值a+1，a，a-2（由大到小排列），这三个特征值中最小的必为零，即a-2=0，由此得到a=2.

例6.10.4 设A为n阶实对称可逆矩阵，A_ij是A=（a_ij）_n×n的行列式A的元素a_ij的代数余子式（i，j=1，2，…，n）以及二次型

（1）记x=（x₁，x₂，…，x_n）^T，把f（x₁，x₂，…，x_n）写成矩阵形式，并证明二次型f（x₁，x₂，…，x_n）的矩阵为A^-1.

（2）问二次型g（x₁，x₂，…，x_n）=x^TAx与f（x₁，x₂，…，x_n）是否有相同的规范形，说明理由.

精解（1）由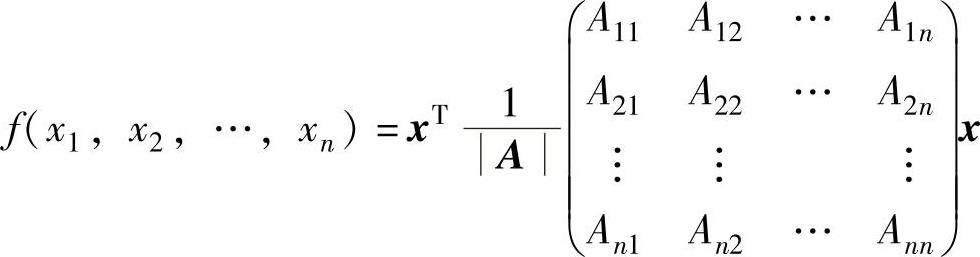

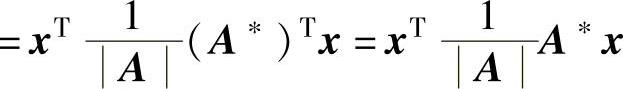
（由于A是对称矩阵，所以A∗也是对称矩阵）

=x^TA^-1x

及A^-1是实对称矩阵知，f（x₁，x₂，…，x_n）的矩阵为A^-1.

（2）由于（A^-1）TAA^-1=（A^T）-1（AA^-1）=A^-1E_n=A^-1，即实对称矩阵A与A^-1合同，所以，二次型g（x₁，x₂，…，x_n）与f（x₁，x₂，…，x_n）具有相同的规范形.