考研数学基础篇全面复习与常考知识点解析

2023-10-27 理论教育版权反馈

【摘要】：，n）为n元二次型.记aji=aij（i，j=1，2，…，xn）=xTAx.2.二次型化标准形的方法如果二次型中只含有变量的平方项，则称这种二次型为标准形.设二次型f（x1，x2，…，xn）T），则它有以下两种化标准形的方法：可逆线性变换法由于对实对称矩阵A，存在可逆矩阵C，使得，所以令x=Cy（可逆线性变换，其中，y=（y1，y2，…，xn）化为标准形d1y21+d2y22+…

【主要内容】

1.二次型的定义及其矩阵表示

称n个变量x₁，x₂，…，x_n的二次齐次函数

f（x₁，x₂，…，x_n）=a₁₁x²₁+2a₁₂x₁x₂+2a₁₃x₁x₃+…+2a_1nx₁x_n+

a₂₂x²₂+2a₂₃x₂x₃+…+2a_2nx₂x_n+…+a_nnx²_n （1）（其中，a_ij是实系数，i，j=1，2，…，n）为n元二次型.

记a_ji=a_ij（i，j=1，2，…，n，i<j），则式（1）可以表示为

f（x₁，x₂，…，x_n）=a₁₁x²₁+a₁₂x₁x₂+a₁₃x₁x₃+…+a_1nx₁x_n+

a₂₁x₂x₁+a₂₂x²₂+a₂₃x₂x₃+…+a_2nx₂x_n+…+

a_n1x_nx₁+a_n2x_nx₂+a_n3x_nx₃+…+a_nnx²_n.

记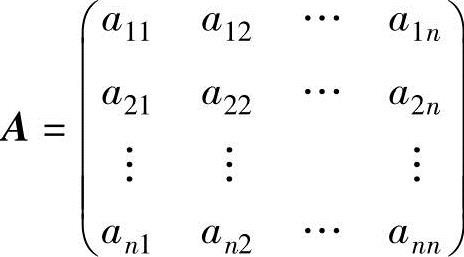（称为二次型（1）的矩阵，它是实对称矩阵，称它的秩r（A）为二次型（1）的秩），x=（x₁，x₂，…，x_n）^T，则二次型（1）有以下的矩阵表示形式：

f（x₁，x₂，…，x_n）=x^TAx.

2.二次型化标准形的方法

如果二次型中只含有变量的平方项（即它的矩阵是对角矩阵），则称这种二次型为标准形.

设二次型f（x₁，x₂，…，x_n）=x^TAx（其中，A是n阶实对称矩阵，x=（x₁，x₂，…，x_n）^T），则它有以下两种化标准形的方法：

（1）可逆线性变换法（也称配方法）由于对实对称矩阵A，存在可逆矩阵C，使得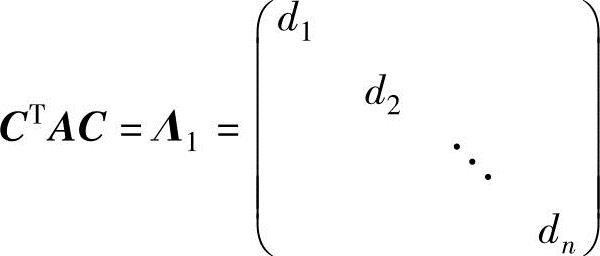，所以令x=Cy（可逆线性变换，其中，y=（y₁，y₂，…，y_n）^T），则

f（x₁，x₂，…，x_n）=y^T（C^TAC）y=d₁y²₁+d₂y²₂+…+d_ny²_n（标准形）.

上述的可逆矩阵可由二次型f（x₁，x₂，…，x_n）经配方得到，具体步骤如下：

（ⅰ）如果f（x₁，x₂，…，x_n）中含有变量x_i（不妨设为x₁）的平方项，则将含x₁的项集中起来，将它们配成平方项，然后用同样的方法对其余变量进行配方，直到将f（x₁，x₂，…，xn）配成平方和的形式，即f（x₁，x₂，…，x_n）=d₁y²₁+d₂y²₂+…+d_ny²_n，由此根据x₁，x₂，…，xn到y1，y2，…，yn之间的可逆线性变换x=Cy可确定可逆矩阵C.

（ⅱ）如果f（x₁，x₂，…，x_n）中不含有各个变量的平方项，则必有某个乘积项的系数不为零，如a_ij≠0，此时可先作变量代换

使f（x₁，x₂，…，x_n）=g（z₁，z₂，…，z_n），而g（z₁，z2，…，z_n）中出现变量的平方项，然后按（ⅰ）中所述的方法令z=C₁y（其中，z=（z₁，z₂，…，z_n）T）将g（z₁，z₂，…，z_n）化为标准形e₁y²₁+e₂y²₂+…+e_ny²_n.复合上述两个可逆线性变换得x=Cy，由此确定可逆矩阵C.

（2）正交变换法

由于对实对称矩阵A，存在正交矩阵Q，使得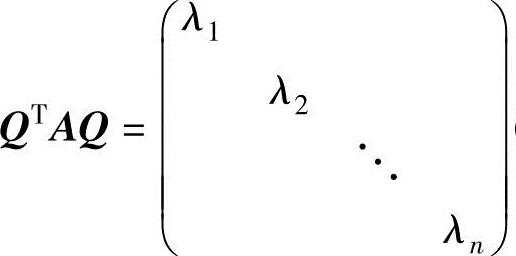（其中λ₁，λ₂，…，λ_n是A的n个特征值），所以令x=Qy（正交变换，其中y=（y₁，y₂，…，y_n）T），则

f（x₁，x₂，…，xn）=y^T（Q^TAQ）y=λ₁y²₁+λ₂y²₂+…+λ_ny²n.

3.矩阵合同

（1）矩阵合同的概念

设A，B都是n阶矩阵.如果存在可逆矩阵C，使得C^TAC=B，则称A与B合同，记为A≃B.

n阶实对称矩阵A必与某个n阶对角矩阵合同，即A可合同对角化.

设A，B，C都是n阶矩阵，则

（ⅰ）A≃A.

（ⅱ）设A≃B，则B≃A.

（ⅲ）设A≃B，B≃C，则A≃C.

（ⅳ）设A≃B，则A^T≃B^T，λA≃λB（λ是常数）.

（ⅴ）设A≃B，则A与B同为可逆或不可逆.

（ⅵ）设A≃B，则当A可逆时，A^-1≃B^-1，A∗≃B∗.

（ⅶ）设A≃B，则A↔B，从而r（A）=r（B）.

注（ⅰ）矩阵等价，相似与合同之间有以下的关系：

设A，B都是n阶矩阵，则

实对称矩阵等价，相似与合同之间有以下的关系：设A，B都是n阶实对称矩阵，则

（2）实对称矩阵合同对角化方法

要将n阶实对称矩阵A合同对角化，实质是寻找可逆矩阵C和对角矩阵Λ，使得C^TAC=Λ，C和Λ可按以下步骤计算：

（ⅰ）构造n元二次型f（x₁，x₂，…，x_n）=x^TAx（其中，x=（x₁，x₂，…，x_n）^T）；

（ⅱ）用配方法将f（x₁，x₂，…，x_n）化为标准形d₁y²₁+d₂y²₂+…+d_ny²_n，由x与y=（y₁，y2，…，yn）^T之间的可逆线性变换x=Cy得可逆矩阵C及对角矩阵

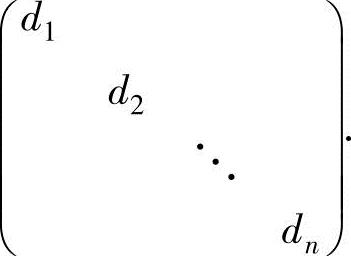
【典型例题】

例6.9.1 已知二次型f（x₁，x₂，x₃）=5x²₁+5x²₂+cx²₃-2x₁x₂+6x₁x₃-6x₂x₃的秩为2，求常数c，并用正交变换将其化为标准形.

精解 f的秩即为f的矩阵A的秩，所以先写出A并对它施行初等行变换.

所以由r（A）=2，得c=3.

为求正交变换x=Qy（其中x=（x₁，x₂，x₃）^T，y=（y₁，y₂，y₃）^T），先求出Q的特征值与对应的特征向量，然后将特征向量正交单位化即可.(www.chuimin.cn)

由

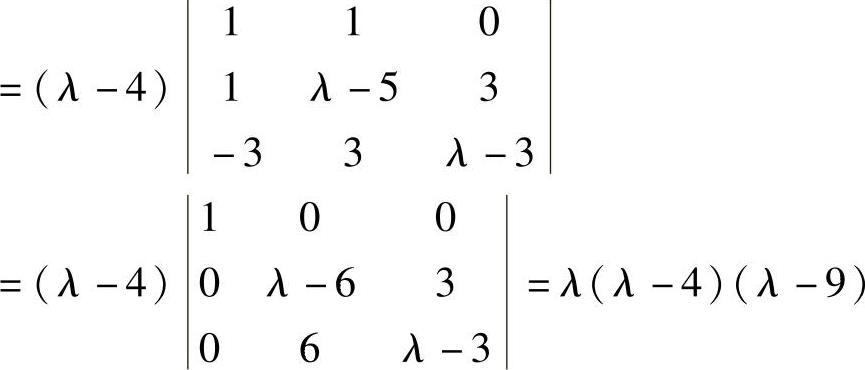
得A的特征值为λ=0，4，9.

设对应λ=0的特征向量为α=（a₁，a₂，a₃）^T，则α满足方程组（0·E₃-A）α=0，即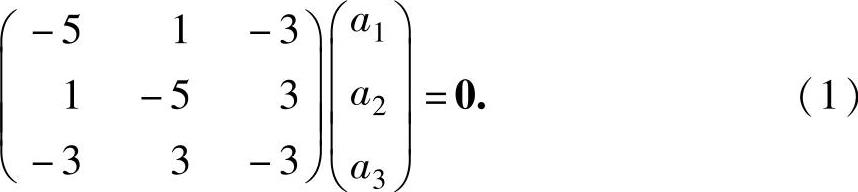

由于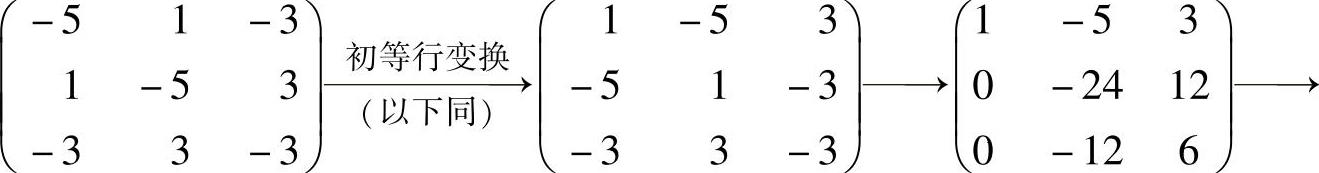

所以，方程组（1）与方程组同解，因此方程组（1）有基础解系（-1，1，

2）T，记ξ₁=（-1，1，2）^T，它即为A的对应λ=0的特征向量.

设对应λ=4的特征向量为β=（b₁，b₂，b₃）^T，则β满足方程组（4E₃-A）β=0，即

由于，所以式（2）有基础解系

（1，1，0）^T，记ξ₂=（1，1，0）^T，它即为A的对应特征值λ=4的特征向量.

设对应λ=9的特征向量为γ=（c₁，c₂，c₃）^T，则由γ与ξ₁和ξ₂都正交有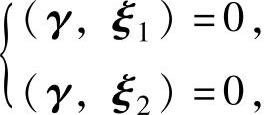即或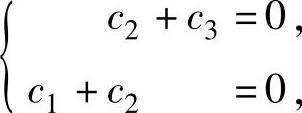

它有基础解系（-1，1，-1）T，记ξ₃=（-1，1，-1）T，它即为A的对应特征值λ=9的特征向量.

ξ₁，ξ₂，ξ₃两两正交，现将它们单位化：

则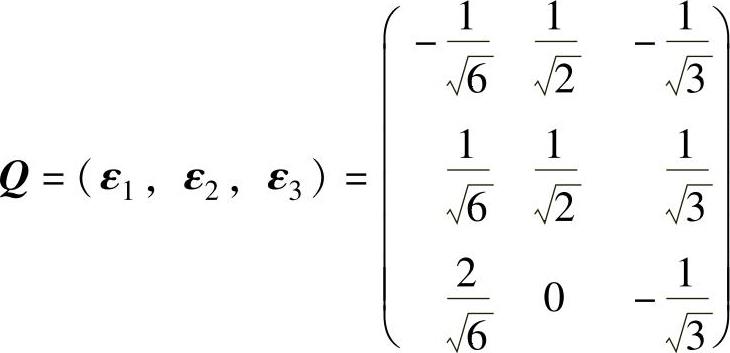（正交矩阵），于是正交变换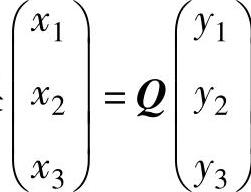将二次型

例6.9.2 用配方法将二次型f（x₁，x₂，x₃）=2x₁x₂+2x₁x₃+2x₂x₃化为标准形，并求出对应的变量之间的可逆线性变换.

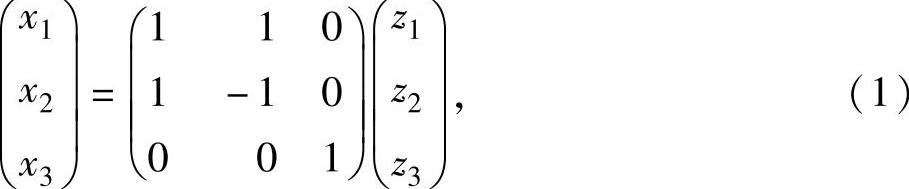精解由于所给二次型中只出现变量的乘积项，不出现平方项，所以需要作变量之间的可逆线性变换：即则

f（x₁，x₂，x₃）=2（z²₁-z²₂）+2（z₁z₃+z₂z₃）+2（z₁z₃-z₂z₃）

=2z²₁-2z²₂+4z₁z₃

=2（z²₁+2z₁z₃+z²₃）-2z²₂-2z²₃

=2（z₁+z₃）²-2z²₂-2z²₃.

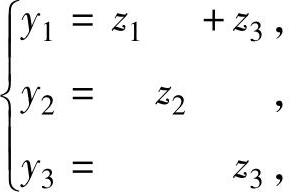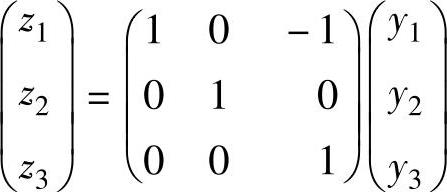令即或，（2）

则f（x₁，x₂，x₃）=2y²₁-2y²₂-2y²₃（标准形）.

将式（2）代入式（1）得x₁，x₂，x₃与y₁，y₂，y₃之间的可逆线性变换为

即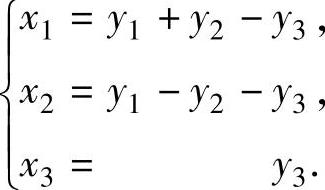

例6.9.3 设二次型f（x₁，x₂，x₃）=x²₁+x²₂+x²₃+2αx₁x₂+2βx₂x₃+2x₁x₃经正交变换x=Qy（x=（x₁，x₂，x₃）^T，y=（y₁，y₂，y₃）^T）后化成标准形为f=y²₂+2y²₃，求常数α，β及正交矩阵Q.

精解由于f（x₁，x₂，x₃）经正交变换后化为标准形f=y²₂+2y²₃，所以f（x₁，x₂，x₃）的矩阵

由此可知A有特征值0，1，2，于是有

，

{，即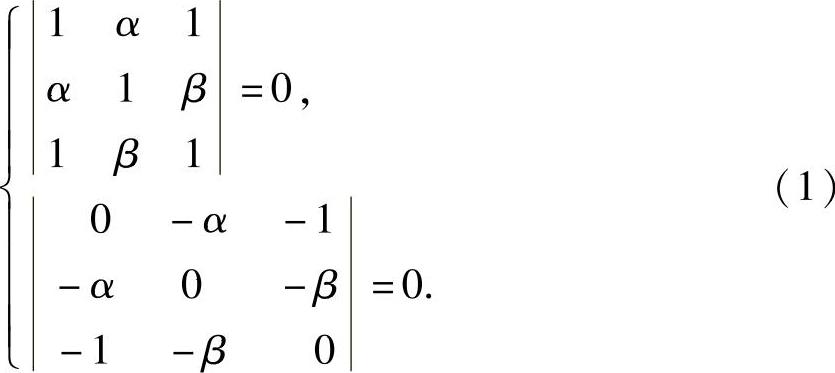由于，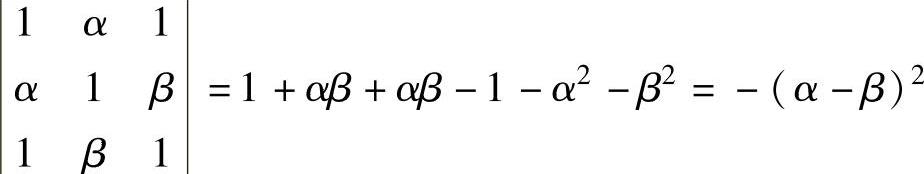

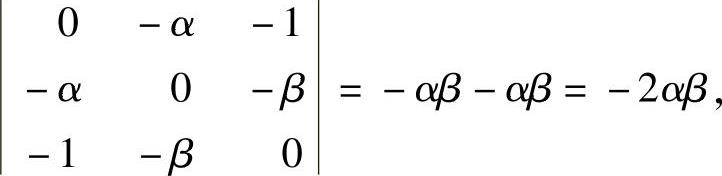
将它们代入式（1）得

解此方程组得α=β=0.于是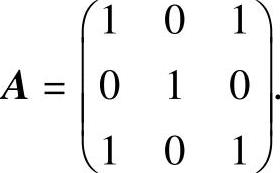

设对应于特征值λ=0的特征向量为α=（a₁，a₂，a₃）^T，则α满足方程组（0·E₃-A）α=0，即

显然，它有基础解系（1，0，-1）^T，记ξ₁=（1，0，-1）^T，它是A的对应于特征值λ=0的特征向量.

设对应于特征值λ=1的特征向量为β=（b₁，b₂，b₃）^T，则β满足方程组（1·E₃-A）β=0，即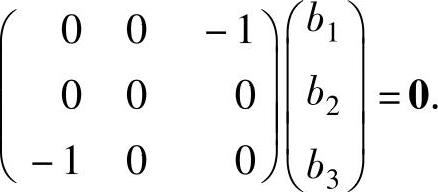显然，它有基础解系（0，1，0）^T，记ξ₂=（0，1，0）^T，它是A的对应于特征值λ=1的特征向量.

设对应于特征值λ=2的特征向量为γ=（c₁，c₂，c₃）^T，则γ满足方程组（2·E₃-A）γ=0，即显然，它有基础解系（1，0，1）^T，记ξ₃=（1，0，1）^T，它是A的对应于特征值λ=2的特征向量.

ξ₁，ξ₂，ξ₃两两正交，现将它们单位化：

于是所求的正交矩阵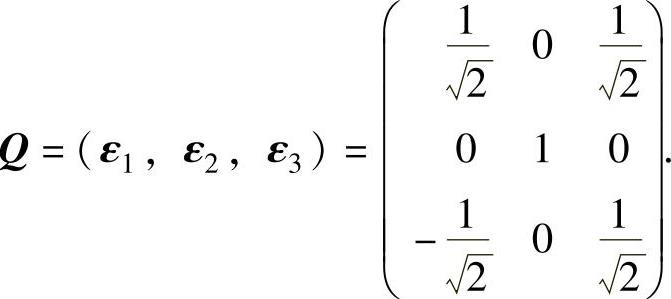

例6.9.4 设实对称矩阵

（1）已知A的一个特征值为3，求实数y；

（2）求可逆矩阵P，使（AP）^T（AP）为对角矩阵.

精解（1）由A有特征值3可得

3E₄-A=0，即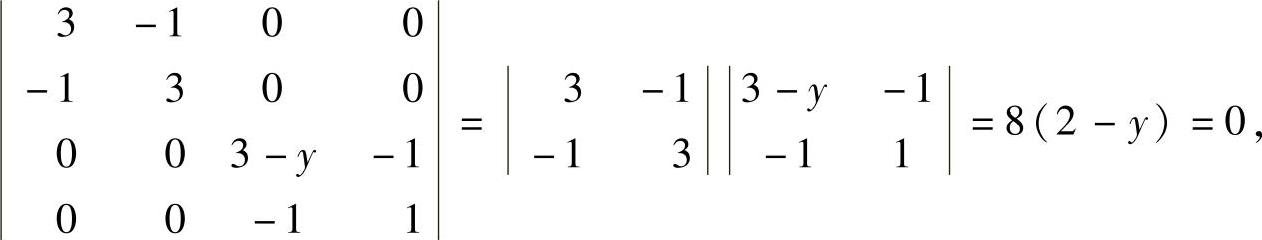

所以，y=2.

（2）由（AP）^T（AP）=P^TA²P知，求可逆矩阵P，使（AP）^T（AP）为对角矩阵，就是求可逆矩阵P，使得

合同对角化，为此构造二次型，且用配方法将其化为标准形：，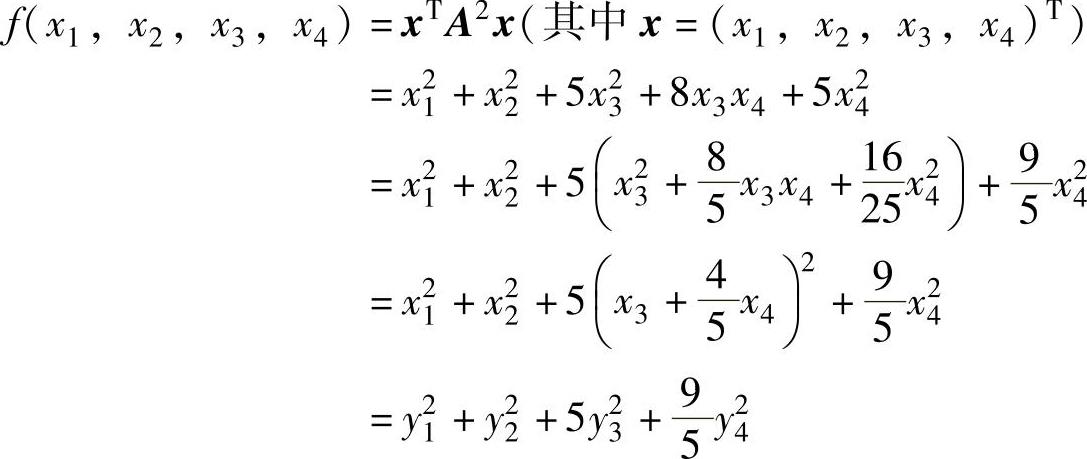

其中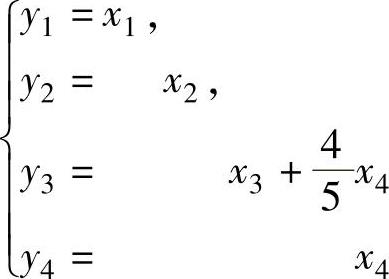即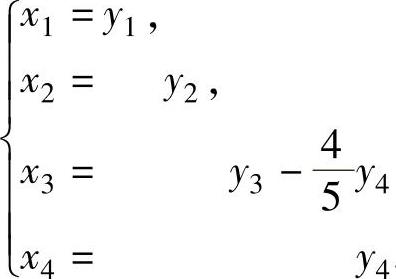，所以所求的可逆矩阵为，.

它使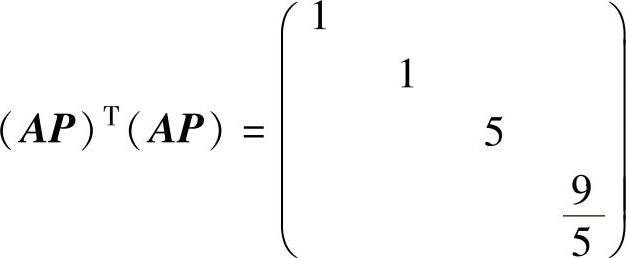（对角矩阵）.

考研数学基础篇全面复习与常考知识点解析

相关推荐