，λn，由于A，B都是实对称矩阵，所以存在可逆矩阵P1和P2，使得于是有P1-1AP1=P2-1BP2，即A=B，或-1A=B.由于P1P2-1是可逆矩阵，所以A～B.......
2023-10-27
矩阵相似对角化条件及意义
【摘要】：【主要内容】1.矩阵可相似对角化的定义设A是n阶矩阵，如果它与n阶对角矩阵Λ相似，则称A可化为相似的对角矩阵，简称A可相似对角化.n阶矩阵A可相似对角化的条件：（1）A有n个互异的特征值是A可相似对角化的充分而非必要条件.（2）A是实对称矩阵是A可相似对角化的充分而非必要条件.（3）A有n个线性无关的特征向量是A可相似对角化的充分必要条件.（4）A的每个ni重特征值λi的特征矩阵λiEn-A都满足
【主要内容】
1.矩阵可相似对角化的定义
设A是n阶矩阵，如果它与n阶对角矩阵Λ相似，则称A可化为相似的对角矩阵，简称A可相似对角化.
n阶矩阵A可相似对角化的条件：
（1）A有n个互异的特征值是A可相似对角化的充分而非必要条件.
（2）A是实对称矩阵是A可相似对角化的充分而非必要条件.
（3）A有n个线性无关的特征向量是A可相似对角化的充分必要条件.
（4）A的每个ni重特征值λi的特征矩阵λiEn-A都满足r（λiEn-A）=n-ni是A可相似对角化的充分必要条件.
2.矩阵相似对角化方法
要将n阶矩阵A相似对角化，实质上是寻找可逆矩阵P和对角矩阵Λ，使得P-1AP=Λ，P和Λ可按以下步骤计算：
（1）计算A的n个特征值λ1，λ2，…，λn（其中可能有相同的）；
（2）逐个计算对应λ1，λ2，…，λn的特征向量，记为ξ1，ξ2，…，ξn；
（3）写出P与Λ：P=（ξ1，ξ2，…，ξn），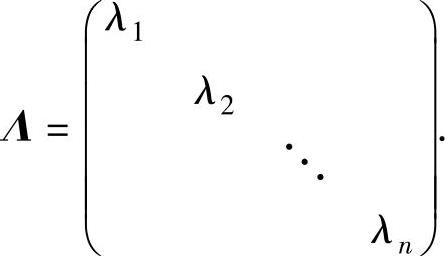
【典型例题】
例6.7.1 （单项选择题）下列矩阵中，不能相似对角化的是（）.
精解 首先，考虑选项A的矩阵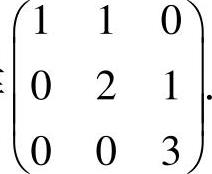
由于它有三个不同的特征值λ=1，2，3，
所以必可相似对角化，故A不能选.
其次，考虑选项B的矩阵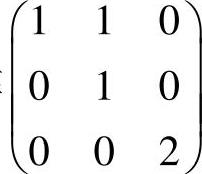
（记为B）.它有二重特征值λ=1，由于1·E3-B
的秩为2，即r（1·E3-B）=2≠3-2（其中，3是矩阵的阶数，2是λ=1的重数），所以选项B的矩阵不可相似对角化.
因此本题选B.
例6.7.2 设三阶矩阵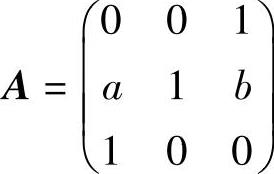
，
都与对角矩阵相似，求参数a，b的值.
精解 通常要确定两个相似矩阵A，B中包含的参数，是利用trA=trB和A=B，但对于本题这种方法却失效，因此从考虑A，B相似对角化入手.
由
=λ2（λ-1）-（λ-1）=（λ+1）（λ-1）2知，A有二重特征值λ=1.此时
，所以，由A可相似对角化知
r（1·E3-A）=（A的3阶数）-（λ=12的重数）=1.从而有a+b=0.（1）
由于用-b-1代替A中元素b，A就变成B，所以由B可相似对角化得
a+（-b-1）=0，即a-b=1.（2）
由式（1）、式（2）得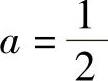
，
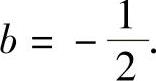
例6.7.3 已知矩阵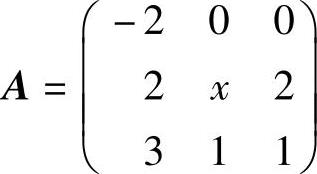
，
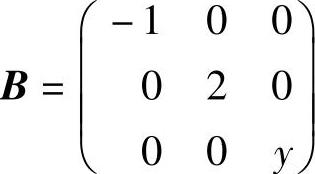相似.
（1）求x，y的值；
（2）求可逆矩阵P，使得P-1AP=B.
精解 （1）由A～B知A与B有相同的特征值及相同的迹，由此算出x与y的值.显然，B有特征值λ=-1，2，y.此外由
知A有一个特征值λ=-2.所以由A与B有相同特征值知y=-2.
由trA=trB，即-2+x+1=-1+2+y得x=2+y=2-2=0.
（2）将x=0代入A得
为计算P，先计算A的特征值与特征向量.
由B有特征值为-1，2，-2得A的特征值λ=-1，2，-2.(www.chuimin.cn)
设A的对应λ=-1的特征向量为x=（x1，x2，x3）T，则x满足（-E3-A）x=0，即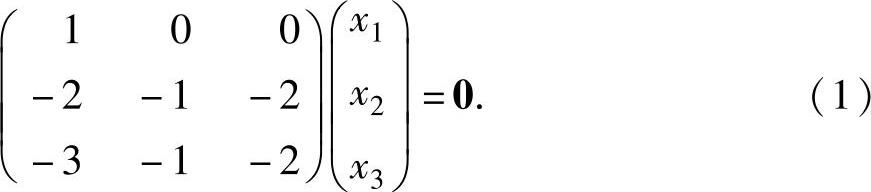
由于
，所以式（1）与方程组
同解，从而式（1）有基础解系（0，-2，1）T.
设A的对应λ=2的特征向量为y=（y1，y2，y3）T，则y满足
（2·E3-A）y=0，即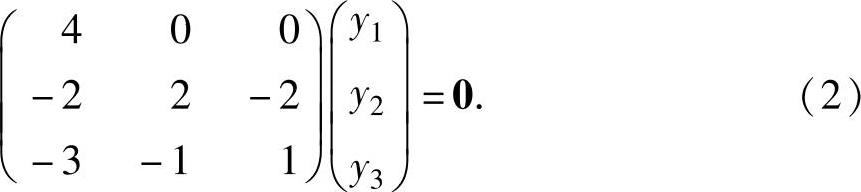
由于
，所
以式（2）与方程组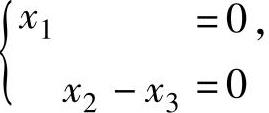
同解.从而式（2）有基础解系（0，1，1）T.
设A的对应λ=-2的特征向量为z=（z1，z2，z3）T，则z满足（-2E3-A）z=0，即
由于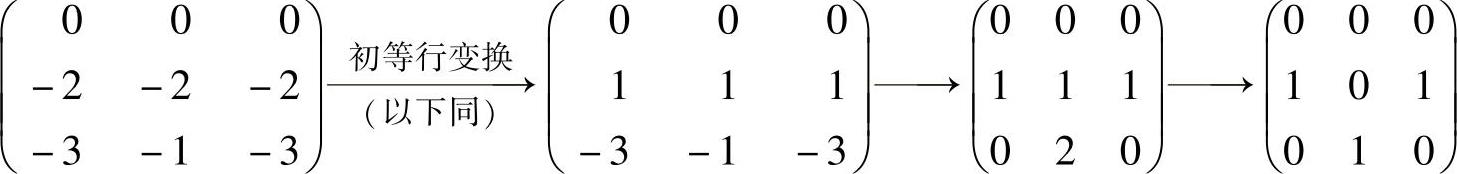
，所以式
（3）与方程组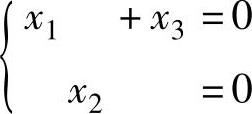
同解，从而式（3）有基础解系（1，0，-1）T.
于是A有特征向量ξ1=（0，-2，1）T，ξ2=（0，1，1）T，ξ3=（1，0，-1）T，它们分别对应特征值-1，2，-2，所以，所求的
它们满足P-1AP=Λ=B.
例6.7.4 设矩阵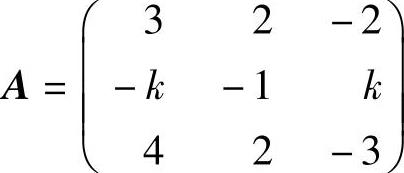
，问当k为何值时，A与对角矩阵相似，即存在
可逆矩阵P，使得P-1AP=Λ（对角矩阵）？并且求P及Λ.
精解 由于trA与|A|中都不含k，所以应从计算A的特征值入手，如有二重的，则其对应的特征矩阵秩应为1，由此确定k的值.而P和Λ则可按常用方法计算.
由于
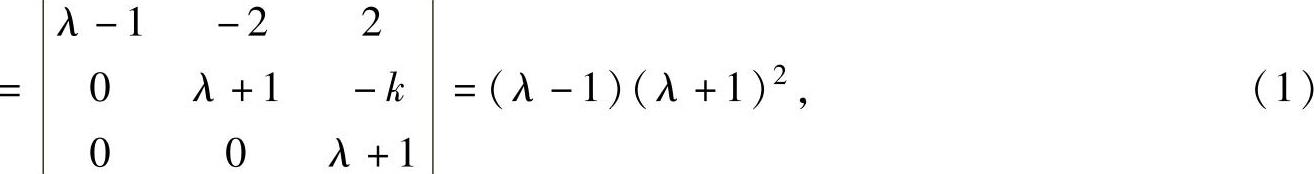
所以，A有二重特征值λ=-1.显然，由
知，当且仅当k=0时，r（-E-A）=（A的3阶数）-（λ=-21的重数），即当且仅当k=0时A可相似对角化.
当k=0时，
，由式（1）知，它有特征值λ=1，-1（二重）.
设对应λ=1的特征向量为x=（x1，x2，x3）T，则x满足
（E3-A）x=0，即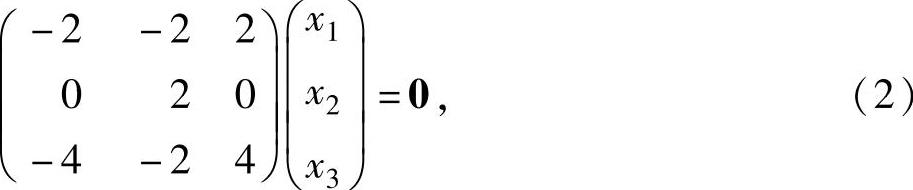
由于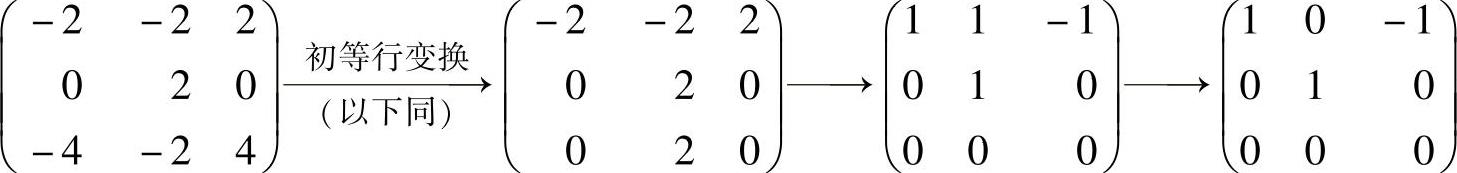
，所以式
（2）与方程组
，
同解，其基础解系为ξ1=（1，0，1）T（即A的对应特征值λ=1的特征向量）.
设对应λ=-1的特征向量为y=（y1，y2，y3）T，则y满足（-E3-A）y=0，即
，或2y1+y2-y3=0，其基础解系为ξ2=（1，-2，0）T和ξ3=（0，1，1）T（即A的对应特征值λ=-1的特征向量）.
于是所求的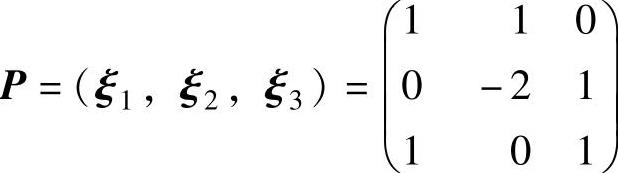
（可逆矩阵）及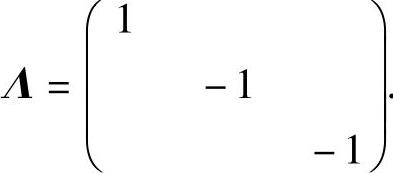
例6.7.5 设3阶矩阵A满足Aαi=iαi（i=1，2，3），其中，α1=（1，2，3）T，α2=（2，-2，1）T，α3=（-2，-1，2）T，求A.
精解 由题设A有三个不同的特征值，知A可相似对角化，因此只要找到满足P-1AP=Λ的P与Λ，即可得到A.
由于A有特征值1，2，3，且α1，α2，α3为对应的特征向量，所以记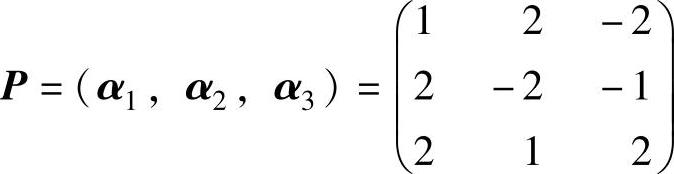
（可逆矩阵）
时，有
，即
由于
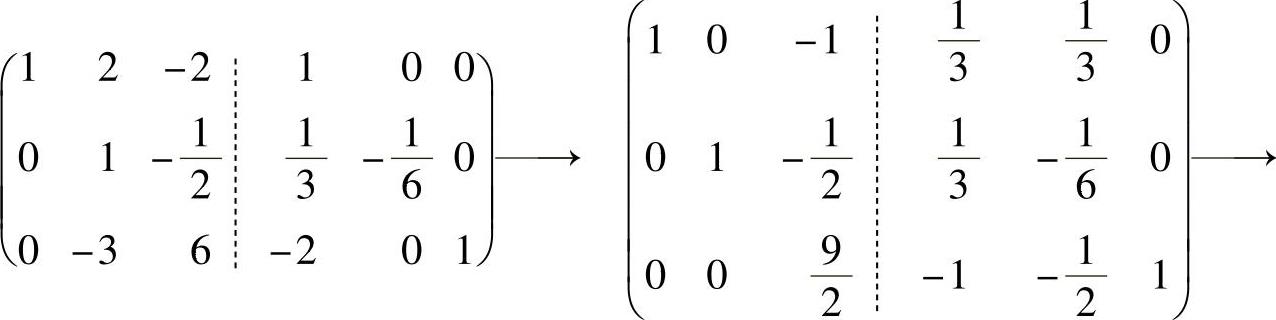
所以，
将式（2）代入式（1）得
有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章
- 详细阅读
-
矩阵相似定义及性质概述详细阅读
1.矩阵相似的定义设A，B都是n阶矩阵.如果存在n阶可逆矩阵P，使得B=P-1AP，则称矩阵A与B相似，也称A与B为相似矩阵，记为A～B.2.矩阵相似的性质设A，B，C都是n阶矩阵，则有以下性质：A～A.如果A～B，则B～A.如果A～B，B～C，则A～C.如果A～B，则AT～BT，Am～Bm，λA～λB，φ～φ（其中，φ（λ）=a0+a1λ+…......
2023-10-27
-
实对称矩阵的合同及相似判定详细阅读
（1）同阶实对称矩阵A，B合同的判定.①用定义法：A，B合同存在可逆矩阵C，使得CTAC＝B.②用正、负惯性指数：A，B合同pA＝pB，qA＝qB.（相同的正、负惯性指数）③用传递性：A合同于C，C合同于B，则A合同于B.【注】同阶矩阵A，B相似的判定.（1）用定义法：A，B相似存在可逆矩阵C，使得C－1AC＝B.（2）用传递性：A相似于C，C相似于B，则A相似于B.（常考C为Λ 的情形）（3）用......
2023-11-21
-
模型相似条件的探讨详细阅读
为保证异重流运动相似，张俊华等、李书霞等 以非恒定异重流运动方程式开展相似分析，并通过水库泥沙模型检验，得出的异重流发生相似条件，利用二维非恒定非均匀流的扩散方程得到异重流挟沙相似条件及异重流连续相似条件分别为:上述公式构成了完整的河道及水库模型相似律。上述公式构成了完整的河道及水库模型相似律。......
2023-06-23
- 详细阅读
-
向量组等价与矩阵等价的区别及条件详细阅读
给出向量组（Ⅰ）：α1，α2，…，αs 线性表示，则称（Ⅰ）与（Ⅱ）等价.其等价的充要条件是r（Ⅰ）＝r（Ⅱ）＝r（Ⅰ，Ⅱ）.向量组等价和矩阵等价是两个不同的概念.矩阵等价要同型，当然行数、列数都要相等；向量组等价要同维，但向量个数可以不等.A，B同型时，ABr＝rPAQ＝B.αi，βj（i＝1，2，…，βt 这两个向量组中的某一个向量组可由另一个向量组线性表出r（α1，α2，…......
2023-11-21
- 详细阅读
-
张宇线性代数9讲：A的相似对角化详细阅读
设n阶矩阵A，若存在n阶可逆矩阵P，使得P－1AP＝Λ，其中Λ 是对角矩阵，则称A可相似对角化，记A～Λ，称Λ 是A 的相似标准形.于是可知，若A可相似对角化，即P－1AP＝Λ，其中P可逆，等式两边同时左乘P，有AP＝PΛ，记由P可逆，则ξ1，ξ2，…＝λn＝0，A的特征值全是零.若A能与对角矩阵Λ 相似，则Λ 的主对角线元素为A......
2023-11-21
相关推荐