同解与公共解-两个线性方程组的数学分析

2023-10-27 理论教育版权反馈

【摘要】：，an）T既是方程组A1x=b1的解，又是方程组A2x=b2的解，则称x=（a1，a2，…，αt，B的行向量组的一个极大线性无关组为β1，β2，…，βs）=r+r

【主要内容】

1.两个线性方程组的同解

设有两个线性方程组A_ix=b_i（i=1，2），其中，A₁，A₂分别是m₁×n，m₂×n矩阵，b₁，b2分别是m₁，m₂维列向量，x是未知的n维列向量.如果A₁x=b₁的任意解都是A₂x=b₂的解，反之也对，则称这两个方程组同解.

设A₁，A₂分别是m₁×n，m₂×n矩阵，则

齐次线性方程组A₁x=0与A₂x=0同解的充分必要条件是它们有相同的基础解系；

非齐次线性方程组A₁x=b₁与A₂x=b₂（其中，b₁、b₂分别为m₁、m₂维列向量，且至少有一个是非零向量）同解的充分必要条件是它们的导出组有相同的基础解系且有一个相同的特解.

2.两个线性方程组的公共解

设有两个线性方程组A_ix=b_i（i=1，2），其中，A₁，A₂分别是m₁×n，m₂×n矩阵，b₁，b2分别是m₁，m₂维列向量，x是未知的n维列向量.如果x=（a₁，a₂，…，a_n）T既是方程组A₁x=b₁的解，又是方程组A₂x=b₂的解，则称x=（a₁，a₂，…，a_n）T是这两个方程组的公共解.

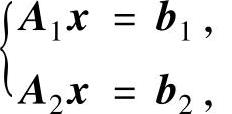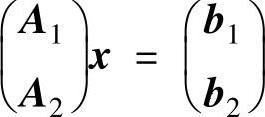方程组A₁x=b₁与A₂x=b₂有公共解的充分必要条件是将这两个方程组合并后的方程组即有解.

【典型例题】

例6.4.1 求使齐次线性方程组

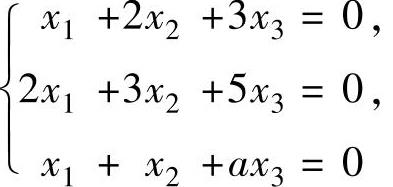（Ⅰ）与（Ⅱ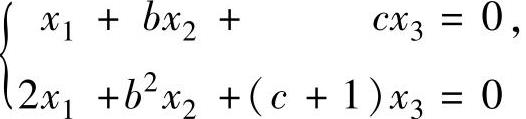）同解的参数a，b，c的值.

精解分别记（Ⅰ）、（Ⅱ）的系数矩阵为A，B，要使（Ⅰ）、（Ⅱ）同解，必须使它们有相同的基础解系，从而有r（A）=r（B）≤2.对A施行初等行变换：

由此可知a=2.此时（Ⅰ）与方程组

同解，所以（Ⅰ）有基础解系（-1，-1，1）T，它也应是（Ⅱ）的基础解系，代入（Ⅱ）得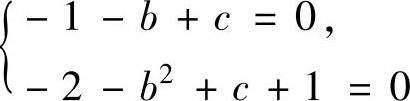

即，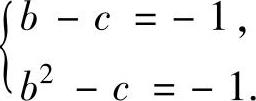

解此方程组得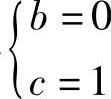，与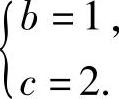

当b=0，c=1时，（Ⅱ）的系数矩阵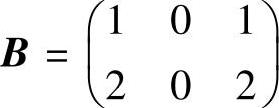的秩为1.此时r（A）≠r（B），所

以b=0，c=1不合适.

当b=1，c=2时，（Ⅱ）的系数矩阵

即此时（Ⅱ）与方程组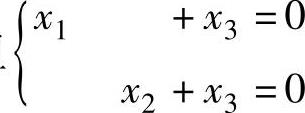，同解，即与（Ⅰ）同解.综上所述，当（Ⅰ）与（Ⅱ）同解时a=2，b=1，c=2.

例6.4.2 已知两个非齐次线性方程组

求使（Ⅰ）与（Ⅱ）同解的m，n，t的值.

精解要使（Ⅰ）与（Ⅱ）同解，只需（Ⅰ）、（Ⅱ）的导出组有相同的基础解系和（Ⅰ）、（Ⅱ）有一个相同的特解，由此确定m，n，t的值.但本题对（Ⅰ）、（Ⅱ）的增广矩阵分别施行一系列初等行变换，使得它们有相同的等价矩阵从而确定m，n，t的值使解题更快捷些.用初等行变换将（Ⅰ）的增广矩阵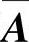化为阶梯形矩阵：

用初等行变换将（Ⅱ）的增广矩阵B化为与式（1）最后一个矩阵相同的矩阵：

要使（Ⅰ）、（Ⅱ）同解，只要使式（1）、式（2）的最后一个矩阵彼此相等即可.由此得到

解此方程组得 m=2，n=4，t=6.

例6.4.3 设4元齐次线性方程组(www.chuimin.cn)

又已知某个4元齐次线性方程组（Ⅱ）的通解为k₁（0，1，1，0）T+k₂（-1，2，2，1）T.求方程组（Ⅰ）与（Ⅱ）的所有非零公共解.

精解由于已知方程组（Ⅱ）的通解，所以只要从中选出满足方程组（Ⅰ）的非零解即可.

由于方程组（Ⅱ）的通解

（x₁，x₂，x₃，x₄）^T=k1（0，1，1，0）^T+k₂（-1，2，2，1）^T

=（-k₂，k₁+2k₂，k₁+2k₂，k₂）^T，即x₁=-k₂，x₂=k₁+2k₂，x₃=k₁+2k₂，x₄=k_2.将它们代入方程组（Ⅰ）得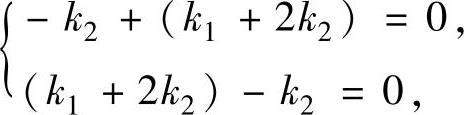即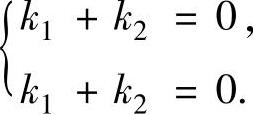

它的所有非零解为k₁=c，k₂=-c（c是任意非零常数）.于是方程组（Ⅰ）与方程组（Ⅱ）的所有非零公共解为

（x₁，x₂，x₃，x₄）^T=c（0，1，1，0）^T-c（-1，2，2，1）^T

=c（1，-1，-1，-1）^T（c是任意非零常数）.

例6.4.4 设齐次线性方程组（Ⅰ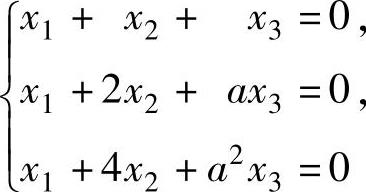）与方程（Ⅱ）x₁+2x₂+x₃=a-1

有公共解，求a的值及所有公共解.

精解从考虑由方程组（Ⅰ）与方程（Ⅱ）组成的线性方程组

有解入手.

对方程组（Ⅲ）的增广矩阵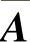施行初等行变换：

由于方程组（Ⅰ）与方程（Ⅱ）有公共解，即方程组（Ⅲ）有解，所以由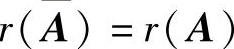（其中，A

是方程组（Ⅲ）的系数矩阵）得a=1（此时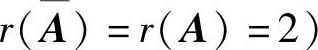或a=2（此时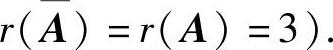

当a=1时，方程组（Ⅲ）与方程组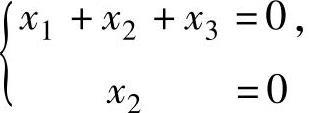同解，它的通解，即方程组（Ⅰ）与

方程（Ⅱ）的公共解为（x₁，x₂，x₃）T=c（-1，0，1）T（c是任意常数）.

当a=2时，方程组（Ⅲ）与方程组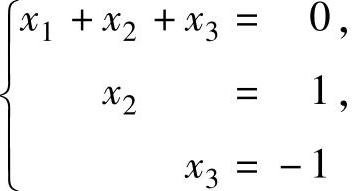同解，它的解，即方程组（Ⅰ）与方程（Ⅱ）的公共解为（x₁，x₂，x₃）T=（0，1，-1）T.

例6.4.5 设A是m×n矩阵，B是n×l矩阵.证明：齐次线性方程组ABx=0与Bx=0是同解方程组的充分必要条件是r（AB）=r（B）.

精解必要性.设方程组ABx=0与Bx=0同解，则它们有相同的基础解系，记其中包含的线性无关解向量的个数为r，于是有l-r（AB）=l-r（B）（其中所给的两个方程组的未知数个数都为l），即r（AB）=r（B）.

充分性.由r（AB）=r（B）知l元方程组ABx=0与l元方程组Bx=0的基础解系中包含的线性无关解向量个数相等.此外，容易知道方程组Bx=0的解都是方程组ABx=0的解，所以方程组Bx=0的基础解系也是方程组ABx=0的基础解系.由此可知，方程组ABx=0与方程组Bx=0有相同的基础解系.因此两个方程组ABx=0与Bx=0同解.

例6.4.6 设A，B都为n阶矩阵，且r（A）+r（B）<n.证明：齐次线性方程组（Ⅰ）Ax=0与（Ⅱ）Bx=0必有非零的公共解.

精解构造齐次线性方程组（Ⅲ），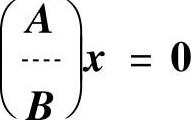

并从计算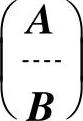的秩入手.

记r（A）=t，r（B）=s，并设A的行向量组的一个极大线性无关组为α₁，α₂，…，α_t，B的行向量组的一个极大线性无关组为β₁，β₂，…，β_s，则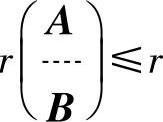（α₁，α₂，…，α_t；β₁，β₂，…，β_s）≤r（α₁，α₂，…，α_t）+r（β₁，β₂，…，β_s）

=r（A）+r（B）<n.

于是，方程组（Ⅲ）有非零解，即两个方程组（Ⅰ）与（Ⅱ）有非零的公共解.

同解与公共解-两个线性方程组的数学分析

相关推荐