，kr，k使得k1α1+k2α2+…+krαr+kβ=0，上式两边左乘βT得k1βTα1+k2βTα2+…+krβTαr+kβTβ=0.由题设知αTiβ=0，即βTαi=0（i=1，2，…，αr，β线性无关.记系数矩阵为A，则A=0，即由此得到a=0，当a=0时，r=1，此时所给方程组通解为（x1，x2，…，1）T.当时，r=n-1，此时所给方程组通解为（x1，x2，…......
2023-10-27
基础篇全面复习与常考知识点解析-练习题五解答
【摘要】：+ks-1αs-1+ksαs=0.此外由题设知（A-E）α1=0，（A-E）α2=α1，即（A-E）2α2=0，（A-E）α3=α2，即（A-E）2α3=α1，（A-E）3α3=0，（A-E）αs-1=αs-2，即（A-E）s-2αs-1=α1，（A-E）s-1αs-1=0，（A-E）αs=αs-1，（A-E）s-1αs=α1，所以k1（A-E）s-1α1+k2（A-E）s-1α2+…
1.单项选择题
（1）D （2）C （3）B （4）C （5）D （6）C
（7）A （8）C （9）C （10）A （11）B （12）C
（13）B （14）D （15）B （16）D （17）D （18）A
（19）A （20）A （21）C （22）D （23）B （24）D
（25）B （26）C （27）B （28）B （29）C （30）D
2.解答题
（2）
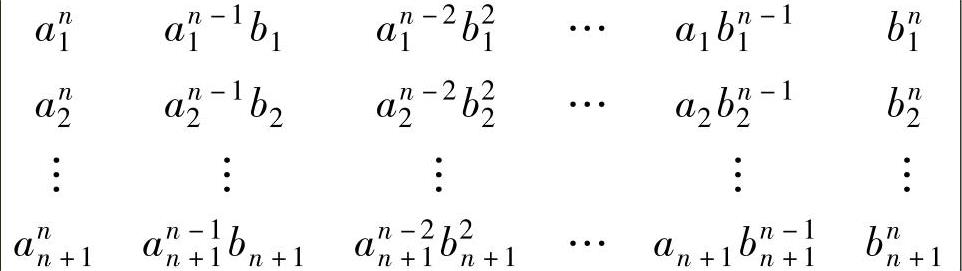
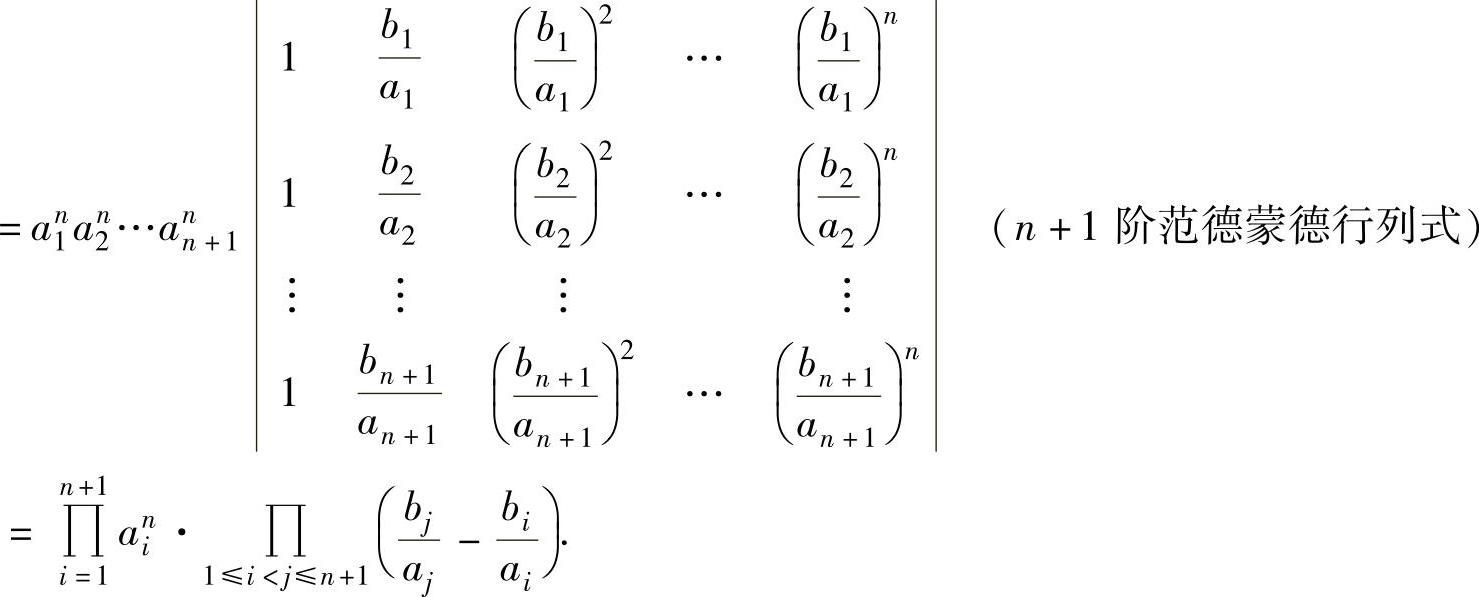
（3）
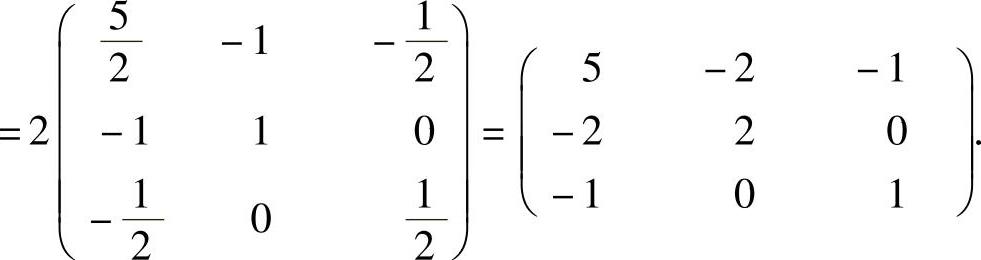
（4）由ABA-1=BA-1+3E4得A∗ABA-1A=A∗BA-1A+3A∗A，即|A|B=A∗B+3|A|E4.由|A|3=|A∗|=8得|A|=2.所以上式成为
（2E4-A∗）B=6E4，即
（5）由
知，A可逆的充分必要条件是a≠0.当a≠0时，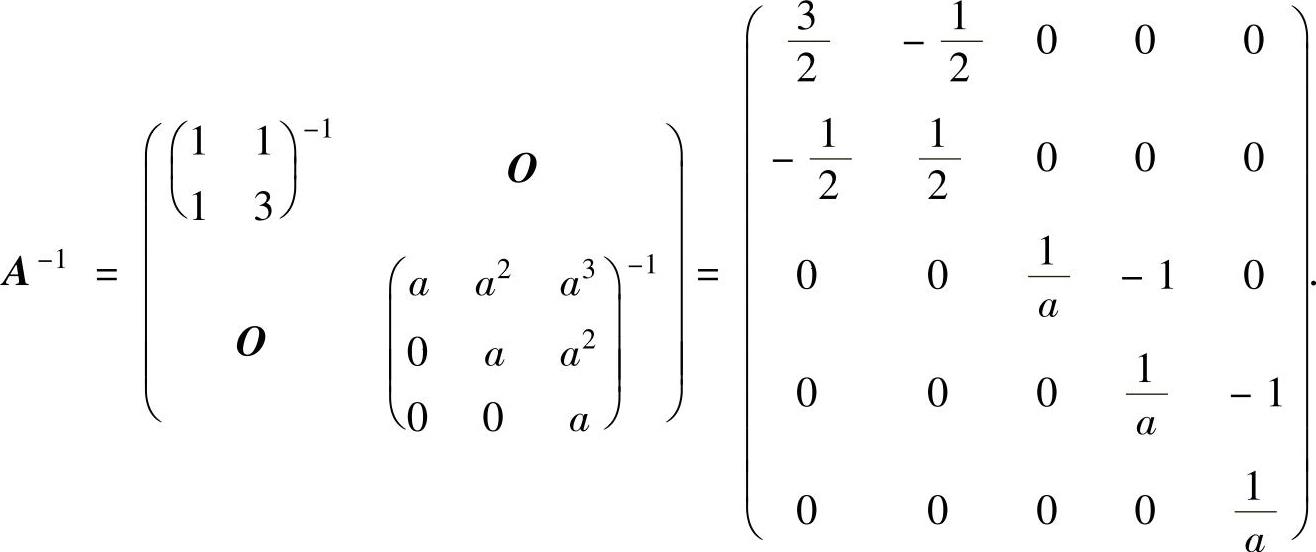
（6）由ABA∗=2BA∗+E3得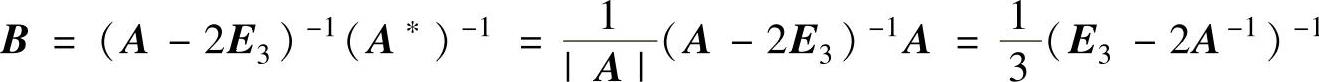
（由于|A|=3），
即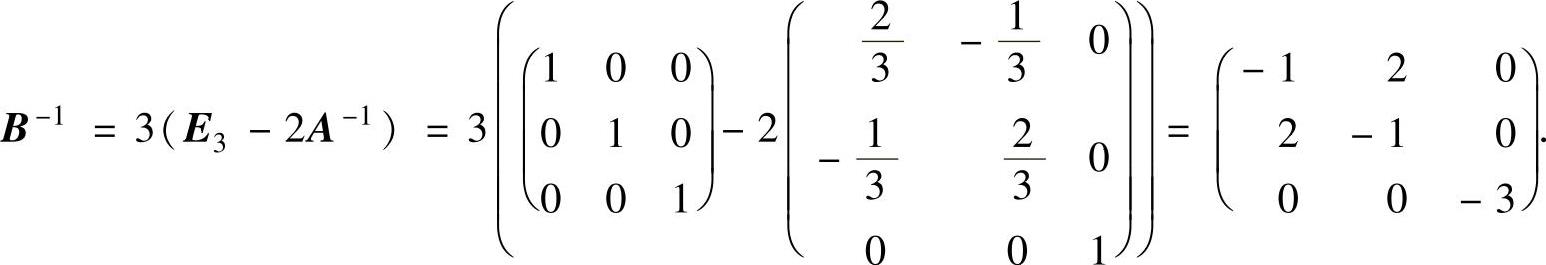
从而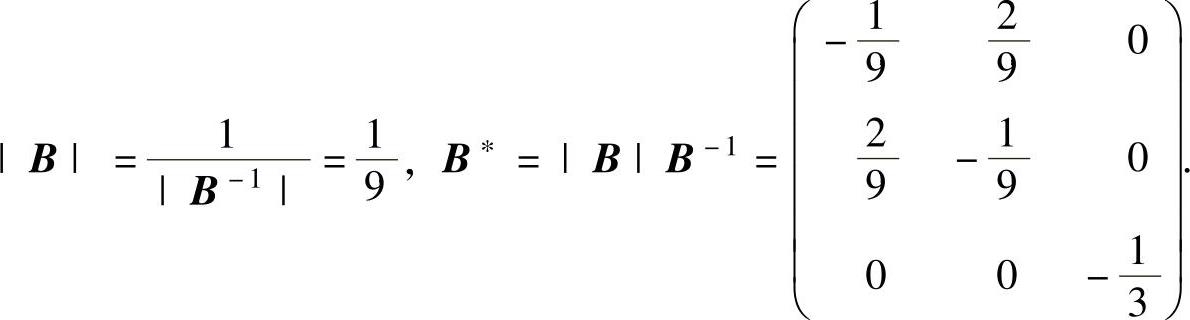
（7）An-2An-1=An-2·A（A-2E3）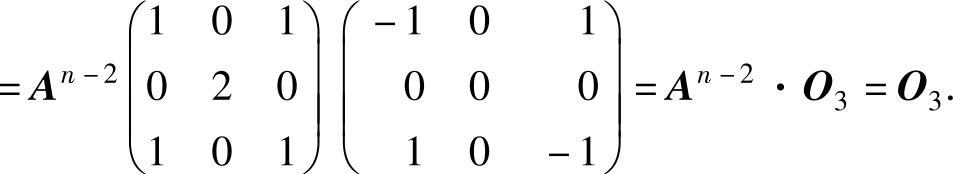
（8）由AB=En，即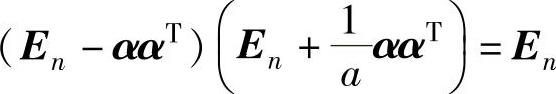
得（2a2+a-1）ααT=On由ααT≠On
得2a2+a-1=0，由此得a=-1.
（9）（ⅰ）由2A-1B=B-4E3得AB-2B-4A=O3，即（AB-2B）-（4A-8E3）=8E3.于是有
所以，A-2E3可逆.
（ⅱ）由（ⅰ）得
（10）由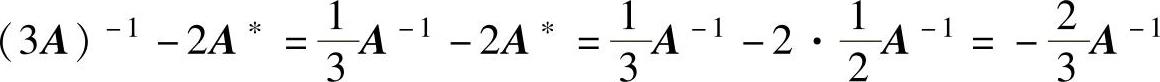
得
（11）由于|B|=10，即B可逆，所以r（AB）=r（A）=2.
（12）（ⅰ）由AB=O3得r（A）+r（B）-3≤r（AB）=0，即r（A）+r（B）≤3.由r（B）>1知r（A）≤1.于是由A的表达式得r（A）=1，从而有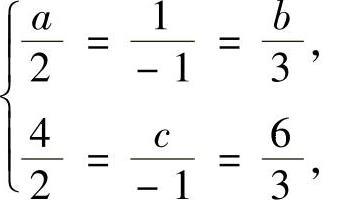
即a=-2，b=-3，c=-2.
（ⅱ）将（ⅰ）中算得的a，b，c代入A得
则
（13）
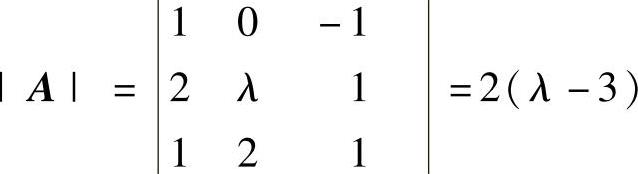，若λ≠3，则A可逆，从而r（AB）=r（B）=
2.与题设矛盾.从而λ=3.
（14）记A的三阶子行列式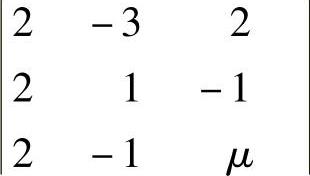
为D3，令D3=0得
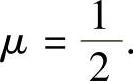所以
时r（A）=3.
当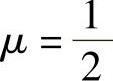
时，对A施行初等行变换.
由此可知，当
，且2λ3-λ2-λ≠0时，即
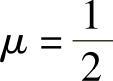，且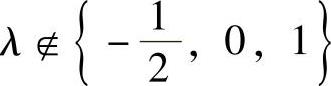
时，r（A）=3；(www.chuimin.cn)
当
时，r（A）=2.
（15）由于B=En-2A-A2=A3-A2-2A=A（A+En）（A-2En），
其中，由A3=En，即A·A2=En知A可逆，且A-1=A2；由A3=En，即A3+En=2En或
知A+En可逆，且
由A3=En，即A3-（2En）3=-7En或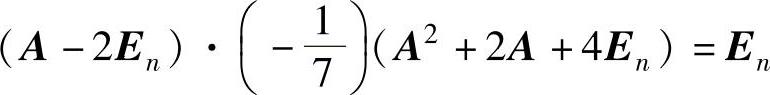
知A-
2En可逆，且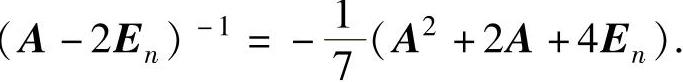
由此可知B可逆，且
（16）由
知r（A）=2，所有的极大线性无关组为α1，α3与α2，α3.
（17）记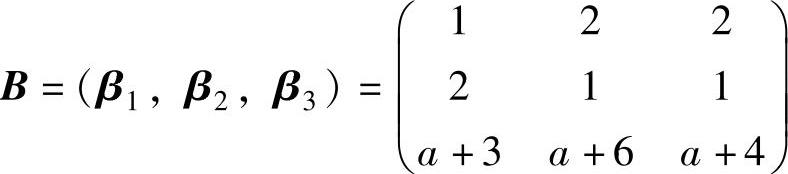
，则|B|=6≠0.所以β1，β2，β3
线性无关，从而（Ⅰ）可由（Ⅱ）线性表示.记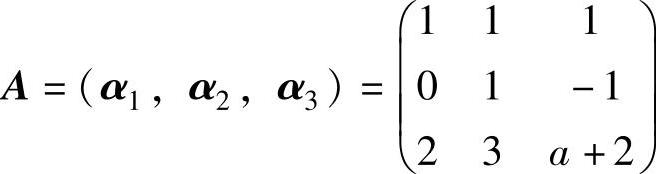
，则|A|=a+1.由此可知，当a≠-1时，α1，
α2，α3线性无关，此时（Ⅱ）可由（Ⅰ）线性表示，即（Ⅰ）与（Ⅱ）等价（当a=-1时由r（α1，α2，α3）<r（β1，β2，β3）知，（Ⅰ）与（Ⅱ）不等价）.
（18）正交化：
β1=α1=（1，1，0，0），
单位化：
α1，α2，α3，α4的正交单位向量组为ε1，ε2，ε3，ε4.
（19）假设存在数k1，k2，…，ks使得k1α1+k2α2+…+ks-1αs-1+ksαs=0.此外由题设知
（A-E）α1=0，
（A-E）α2=α1，即（A-E）2α2=0，
（A-E）α3=α2，即（A-E）2α3=α1，（A-E）3α3=0，
︙
（A-E）αs-1=αs-2，即（A-E）s-2αs-1=α1，（A-E）s-1αs-1=0，
（A-E）αs=αs-1，（A-E）s-1αs=α1，
所以
k1（A-E）s-1α1+k2（A-E）s-1α2+…+ks-1（A-E）s-1αs-1+ks（A-E）s-1αs=0，
即 ksα1=0.由此得ks=0.从而有
k1α1+k2α2+…+ks-1αs-1=0.
于是同样可证 ks-1=ks-2=…=k1=0.因此α1，α2，…，αs线性无关.
（20）由r（B）≥r（AB）=m，r（B）≤n≤m知r（B）=m=B的列数，所以B的列向量组线性无关.
（21）由
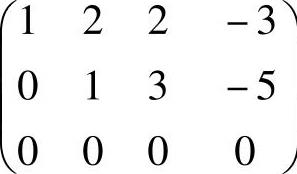知，β1=-4α1+3α2，β2=7α1-5α2.所以，对于不全为零的k1，k2，非零
向量k1β1+k2β2=（-4k1+7k2）α1+（3k1-5k2）α2可以由β1，β2线性表示，也可由α1，α2线性表示.因此所求的非零向量为
有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章
- 详细阅读
- 详细阅读
-
考研数学基础篇全面复习与常考知识点解析详细阅读
，n）为n元二次型.记aji=aij（i，j=1，2，…，xn）=xTAx.2.二次型化标准形的方法如果二次型中只含有变量的平方项，则称这种二次型为标准形.设二次型f（x1，x2，…，xn）T），则它有以下两种化标准形的方法：可逆线性变换法由于对实对称矩阵A，存在可逆矩阵C，使得，所以令x=Cy（可逆线性变换，其中，y=（y1，y2，…，xn）化为标准形d1y21+d2y22+…......
2023-10-27
-
方程实根个数判定-基础篇全面复习与常考知识点详细阅读
【主要内容】1.设函数f（x）在[a，b]上连续，且f（a）f（b）<0，则方程f（x）=0在（a，b）内有实根.这一结论有各种推广形式，例如，（1）设函数f（x）在（a，b）内连续，且，则方程f（x）=0在（a，b）内有实根.（2）设函数f（x）在[a，+∞）上连续，且，则方程f（x）=0在[a，+∞）上有实根.2.设f（x）是[a，b]上的连续单调函数，且f（a）f（b）<0，则方程f（x）=......
2023-10-27
-
罗尔定理和应用-基础篇全面复习与常考知识点解详细阅读
【主要内容】1.罗尔定理设函数f（x）在[a，b]上连续，在（a，b）内可导，且f（a）=f（b），则存在ξ∈（a，b），使得f′（ξ）=0.罗尔定理有各种推广形式，例如（1）设函数f（x）在（a，b）内可导，且与存在且相等，则存在ξ∈（a，b），使得f′（ξ）=0.（2）设函数f（x）在[a，+∞）上连续，在（a，+∞）上可导，且，则存在ξ∈（a，+∞），使得f′（ξ）=0.2.罗尔定理应用方法......
2023-10-27
- 详细阅读
-
定积分不等式证明-基础篇全面复习与常考知识点详细阅读
【主要内容】含定积分的不等式的常见证明方法是导数方法，即将欲证不等式中所包含的定积分上限字母换成x（如果包含的定积分多于一个，则选择其中一个，将其上限字母换成x），同时将该不等式中与此相同的字母都换成x，得到一个函数不等式，然后用导数方法证明这个函数不等式成立，由此即证得欲证的不等式.【典型例题】例2.9.1 设函数f（x）在[0，+∞）上连续且单调增加.证明：满足0
2023-10-27
-
2015考研数学全面复习与常考知识点解析详细阅读
为了帮助同学们在考研复习时，能够在较为紧张的时间安排下，有效加深概念与理论的理解，熟练掌握常用的解题方法与技巧，针对考生的实际需要，我社特组织出版了由北京邮电大学陈启浩教授编写的“天勤数学考研系列”丛书.这套丛书2013年出版时曾用名“考研数学复习指导系列丛书”.本套丛书分别针对参加数学一、数学二和数学三考试的同学，其中针对数学三考试的包括四本书，分别是：《2015考研数学（三）真题篇 十年真题精......
2023-10-27
相关推荐