向量组的标准正交化与正交矩阵解析

2023-10-27 理论教育版权反馈

【摘要】：+anbn=0时，称α与β正交.2.向量组的单位正交化单位正交向量组设α1，α2，…，αm单位正交化的施密特方法如下：（ⅰ）正交化：取β1=α1，（ⅱ）单位化：由此得到的ε1，ε2，…

【主要内容】

1.向量内积的概念

（1）向量的内积

设n维向量α=（a₁，a₂，…，a_n）T，β=（b₁，b₂，…，b_n）T，则称数

为α与β的内积.

向量内积的性质：设α，β，γ都是n维向量，则有

（ⅰ）（α，β）=（β，α）；

（ⅱ）（α+β，γ）=（α，γ）+（β，γ）；

（ⅲ）（kα，β）=（α，kβ）=k（α，β）（k为常数）；

（ⅳ）（α，α）≥0.称为向量α的模，且‖α‖=0的充分必要条件是

α=0.

（2）向量正交的概念

设α=（a₁，a₂，…，a_n）T，β=（b₁，b₂，…，b_n）T都是n维非零向量，则当（α，β）=0，即a₁b₁+a₂b₂+…+a_nb_n=0时，称α与β正交.

2.向量组的单位正交化

（1）单位正交向量组

设α₁，α₂，…，α_m是向量组，如果它们是两两正交的非零向量，则称α₁，α₂，…，α_m是正交向量组.

设α₁，α₂，…，α_m是正交向量组，如果其中每个向量的模都为1，则称α₁，α₂，…，α_m是单位正交向量组.

单位正交向量组的性质：设α₁，α₂，…，α_m是单位正交向量组，则

（ⅰ）；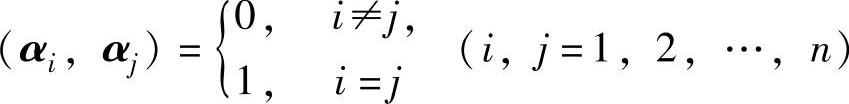

（ⅱ）α₁，α₂，…，α_m线性无关，即r（α₁，α₂，…，α_m）=m.

（2）向量组单位正交化方法（施密特单位正交化）

设向量组α₁，α₂，…，α_m线性无关，则存在与该向量组等价的单位正交向量组ε₁，ε₂，…，ε_m.由α₁，α₂，…，α_m到ε₁，ε₂，…，εm的过程称为α₁，α₂，…，α_m的单位正交化.

线性无关向量组α₁，α₂，…，α_m单位正交化的施密特方法如下：

（ⅰ）正交化：取

β₁=α₁，

（ⅱ）单位化：

由此得到的ε₁，ε₂，…，ε_m是α₁，α₂，…，α_m的单位正交化向量组.

3.正交矩阵

设A是n阶实矩阵.如果A^TA=E_n，则称A是n阶正交矩阵.

正交矩阵的性质：设A，B都是n阶正交矩阵，则

（1）A可逆，且A^-1=A^T，从而有AA^T=E_n；

（2）|A|=-1或1；

（3）A^T与A^-1都是正交矩阵；

（4）A的列向量组与行向量组都是单位正交向量组.

【典型例题】

例5.9.1 试将向量组α₁=（2，0，1）^T，α₂=（0，1，0）^T，α₃=（1，0，2）T单位正交化.

精解首先正交化：注意α₁与α₂正交，所以可取(www.chuimin.cn)

β₁=α₁=（2，0，1）^T，β₂=α₂=（0，1，0）^T，

且由施密特正交化方法知

其次单位化：取

ε₁，ε₂，ε₃即为α₁，α₂，α₃的单位正交化向量组.

例5.9.2 设α₁，α₂，α₃与β₁，β₂是两个线性无关的向量组，且（α_i，β_j）=0（i=1，2，3；j=1，2）.证明：向量组α₁，α₂，α₃，β₁，β₂线性无关.

精解用向量组线性无关的定义证明.

假设存在数λ₁，λ₂，λ₃，μ₁，μ₂，使得

λ₁α₁+λ₂α₂+λ₃α₃+μ₁β₁+μ₂β₂=0，（1）即λ₁α₁+λ₂α₂+λ₃α₃=-μ₁β₁-μ₂β₂.（2）于是，（λ₁α₁+λ₂α₂+λ₃α₃，λ₁α₁+λ₂α₂+λ₃α₃）

=（λ₁α₁+λ₂α₂+λ₃α₃，-μ₁β₁-μ₂β₂）

=λ_1μ1（α₁，β₁）-λ₂μ₁（α₂，β₁）-λ₃μ₁（α₃，β₁）-λ₁μ₂（α₁，β₂）-

λ_2μ2（α₂，β₂）-λ₃μ₂（α₃，β₂）

=0（利用题设（α_i，β_j）=0，i=1，2，3；j=1，2）.

由此得到

λ₁α₁+λ₂α₂+λ₃α₃=0.（3）

由于α₁，α₂，α₃线性无关，所以由式（3）得λ₁=λ₂=λ₃=0.将它代入式（2）得

μ₁β₁+μ₂β₂=0.

由于β₁，β₂线性无关，所以μ₁=μ₂=0.

由上可知，当且仅当λ₁=λ₂=λ₃=μ₁=μ₂=0时式（1）成立，所以α₁，α₂，α₃，β₁，β₂线性无关.

例5.9.3 设A，B都是n阶正交矩阵，且|A|+|B|=0，求行列式|A+B|的值.

精解利用正交矩阵的定义与性质计算行列式|A+B|.

由 A，B都是正交矩阵，知

AA^T=E_n，B^TB=E_n，所以

A+B=AE_n+E_nB=AB^TB+AA^TB

=A（B^T+A^T）B=A（A+B）^TB.

从而 |A+B|=|A||（A+B）^T||B|=-|A|²|A+B|（利用|A|+|B|=0，即|B|=-|A|），

即 |A+B|（1+|A|²）=0.

由于 1+|A|²≠0，所以由上式得|A+B|=0.

例5.9.4 设A是实对称矩阵，B是实反对称矩阵，AB=BA，且A-B是可逆矩阵.证明：（A+B）（A-B）^-1是正交矩阵.

精解由题设知A^T=A，B^T=-B，从而由A-B可逆知A+B=（A-B）^T可逆.从而由

[（A+B）（A-B）^-1]^T[（A+B）（A-B）^-1]

=[（A-B）^-1]^T[（A+B）^T（A+B）]（A-B）^-1

=[（A-B）^T]^-1[（A-B）（A+B）]（A-B）^-1

=（A+B）^-1（A+B）（A-B）（A-B）^-1

（由题设AB=BA知（A-B）（A+B）=（A+B）（A-B））

=[（A+B）^-1（A+B）][（A-B）（A-B）^-1]=E_n知（A+B）（A-B）^-1是正交矩阵.

向量组的标准正交化与正交矩阵解析

相关推荐