定义1 线性定常系统的传递函数，定义为零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。传递函数是复变量s的有理真分式函数，具有复变函数的所有性质。传递函数是系统或元件数学模型的另一种形式，是一种用系统参数表示输出量与输入量之间关系的表达式。传递函数与微分方程有相通性。下面举例说明求取简单环节的传递函数的步骤。......
2025-09-29
矩阵秩的定义及性质分析
【摘要】：【主要内容】1.矩阵秩的定义设A是m×n矩阵，则称A的不为零的子行列式（简称子式）的最高阶数为A的秩，记为r（A），其中，A的k（k≤min{m，n}）阶子式是指A的k行k列交叉位置的元素构成的k阶行列式.零矩阵的秩定义为0.2.矩阵秩的性质（1）设A是m×n矩阵，则0≤r（A）≤min{m，n}.（2）设A是m×n矩阵，k是常数，则（3）初等变换不改变矩阵的秩，即等价矩阵的秩相等.（4）设A，B
【主要内容】
1.矩阵秩的定义
设A是m×n矩阵，则称A的不为零的子行列式（简称子式）的最高阶数为A的秩，记为r（A），其中，A的k（k≤min{m，n}）阶子式是指A的k行k列交叉位置的元素构成的k阶行列式.
零矩阵的秩定义为0.
2.矩阵秩的性质
（1）设A是m×n矩阵，则0≤r（A）≤min{m，n}.
（2）设A是m×n矩阵，k是常数，则
（3）初等变换不改变矩阵的秩，即等价矩阵的秩相等.
（4）设A，B都是m×n矩阵，则r（A+B）≤r（A）+r（B）.
（5）设A，B分别是m×s，s×n矩阵，则r（A）+r（B）-s≤r（AB）≤min{r（A），r（B）}.
（6）设A是n阶矩阵，则A可逆的充分必要条件是r（A）=n.
（7）分块矩阵
的秩都为r（A）+r（B）.
3.矩阵秩的计算
通常，用以下的初等行变换方法计算矩阵的秩：
设A是m×n矩阵，经过一系列初等行变换后成为阶梯形矩阵B，则r（A）等于B中非零行的个数，其中，满足以下条件的矩阵称为阶梯形矩阵：
（1）元素全为零的行（称为零行）在矩阵的最下方.
（2）对于非零行，第i+1行的由左至右的第一个非零元素的列标必大于第i行由左至右的第一个非零元素的列标.例如
都是阶梯形矩阵.
【典型例题】
例5.6.1 （单项选择题）设A是m×n矩阵，B是n×m矩阵，则（ ）.
A.当m>n时，|AB|≠0 B.当m>n时，|AB|=0
C.当m<n时，|AB|≠0 D.当m<n时，|AB|=0
精解 显然，AB是m阶矩阵.由r（AB）≤min{m，n}知，当m>n时有r（AB）≤n<m，即AB的秩小于它的阶数，所以|AB|=0.
因此本题选B.
例5.6.2 已知
，P为三阶非零矩阵，且PQ=O3，则（ ）.(https://www.chuimin.cn)
A.t=6时，P的秩必为1 B.t=6时，P的秩必为2
C.t≠6时，P的秩必为1 D.t≠6时，P的秩必为2
精解 当t≠6时，由
知r（Q）=2.
此外，由PQ=O3知r（P）+r（Q）-3≤r（PQ）=0，即0<r（P）≤1（利用P是非零矩阵和r（Q）=2）.由此得到r（P）=1.
因此本题选C.
例5.6.3 求矩阵A的秩，其中
精解 利用初等行变换法计算A的秩.
所以，当λ-3=0，即λ=3时，由
知r（A）=2.此外，当λ≠3时，由
知 r（A）=3（这是因为
例5.6.4 设矩阵
的秩为3，求a，b的取值范围.
精解 用初等行变换法将A化为阶梯形矩阵，然后根据r（A）=3，确定a，b的值.
于是，由r（A）=3知，a，b应满足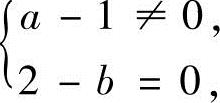
或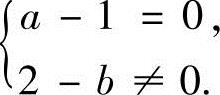
所以，取值范围是a≠1且b=2，或a=1且b≠2.
例5.6.5 设A，B都是n阶矩阵，且ABA=B-1.证明：
r（En+AB）+r（En-AB）=n.
精解 利用矩阵秩的性质证明
r（En+AB）+r（En-AB）≤n和r（En+AB）+r（En-AB）≥n同时成立即可.
由ABA=B-1得ABAB=En，所以
（En+AB）（En-AB）=En+AB-AB-ABAB=On.从而有
r（En+AB）+r（En-AB）-n≤r（（En+AB）（En-AB））=0，即r（En+AB）+r（En-AB）≤n.（1）
此外，r（En+AB）+r（En-AB）≥r（（En+AB）+（En-AB））=r（2En）=n，即r（En+AB）+r（En-AB）≥n.（2）
由式（1）和式（2）得
r（En+AB）+r（En-AB）=n.
相关文章
- 详细阅读
-
高等数学：二重极限定义及性质详细阅读
定义2 设二元函数点f（x，y）在点P0（x0，y0）的某邻域内有定义（点P0可以除外），如果该邻域内的点P（x，y）以任意方式无限趋于点P0（x0，y0）时，对应的函数值f（x，y）无限接近于一个确定的常数A，则称常数A为函数f（x，y）当（x，y）→（x0，y0）时的极限，记作为了区别于一元函数的极限，我们把二元函数的极限叫作二重极限.必须注意，所谓二重极限存在，是指点P（x，y）以任何方式趋......
2025-09-30
-
济南地区石窟与摩崖造像的题材及性质分析详细阅读
济南地区北朝石窟像，据崖面遗存和以往的著录，共有题记10条。从上述材料来看，济南地区石窟造像前后大约出现过9种题材。根据现存的题记资料，济南地区北朝石窟造像主要流行弥勒题材，相比之下，龙门北朝造像虽然弥勒数量也较大，但各期造像总体上仍是以常见的释迦像占主导地位。这是当时济南石窟造像如此流行弥勒题材的一个重要的社会原因。......
2025-09-29
-
保险的定义及分类的分析介绍详细阅读
保险正是针对危险而建立的一种经济制度。然而，保险也不可能对一切危险都予以承保。因此，将来确定发生的危险、已经发生的危险事故、投机性危险等均不被列入保险的适用范围。一旦发生被保险标的损失，由保险基金加以赔偿。人身保险是指以人的生命、身体或健康为保险标的的一种保险，如人寿保险、健康保险、意外伤害保险。原保险又称“第一次保险”“基础保险”，是指保险人对被保险人因保险事故所致损害承担......
2025-09-29
-
搬运任务的定义及要素分析详细阅读
表3.6列出了各种几何形状工件的三种输送形式。图3.11抓取的基本形式图3.12在箱体中三个摆放维度未分拣的工件然而，由于工件本身具有平移和旋转自由度或定向选项，因此从另一方面来说，其取代了输送形式。表3.7工件在预定或定位上的自由度定义中的每个顺序或定位程度以0～3的级别进行评估。图3.16硬币的标志图3.17在不同传送带上工件在运输中的状态改变在生产工件的运输过程中，重要的是确保工件保持其预定状态。......
2025-09-29
-
颗粒污泥的性质分析详细阅读
成熟的颗粒污泥，VSS/SS一般为7%～80%，但根据废水性质其范围可在30%～90%。一般来说，反应器沿高度的群落演替遵循9.3.5中所述规律，而单一颗粒污泥的生物构成遵循生物代谢规律，即产酸细菌主要在颗粒表面，产甲烷细菌主要在颗粒内部。......
2025-09-29
-
连续介质的定义及特点分析详细阅读
多孔介质特征体元由两部分构成，即孔隙度和连续介质。如图1.2所示，称体积ΔV0为多孔介质在数学点M处的特征体元，即多孔介质特征体元。孔隙度为连续函数时，多孔介质便成为连续多孔介质，简称连续介质。应当注意的是，连续流体和连续介质模型也是有局限性的。在这些情况下，连续介质和连续流体模型不能原封不动的套用。图1.2多孔介质孔隙度的定义......
2025-09-29
-
矩阵式变频电路的分析介绍详细阅读
图5.20构造输出电压时可利用的输入电压部分利用对开关S11、S12和S13的控制构造输出电压uu 时，为了防止输入电源短路，在任何时候只能有一个开关接通。在矩阵式变频电路中，9 个开关的通断情况决定后，即调制矩阵σ 中各元素确定后，输入电流ia、ib、ic 和输出电流iu、iv、iw 的关系也就确定了。......
2025-09-29
相关推荐