【主要内容】1.矩阵的初等变换矩阵的下列三种变换称为矩阵的初等行（列）变换：（1）互换矩阵的两行（两列）.（2）用一个非零常数c乘矩阵的某行（某列），即用c乘某行（某列）的每个元素.（3）矩阵某行（某列）的k倍加到另一行（另一列），即某行（某列）的每个元素的k倍，加到另一行（另一列）的对应元素.矩阵的初等行变换与初等列变换，总称矩阵的初等变换.2.初等矩阵单位矩阵经过一次初等变换所得到的矩阵，称为......
2023-10-27
伴随矩阵与矩阵求逆运算
【摘要】：1.伴随矩阵设A是n阶矩阵，则称为A的伴随矩阵，其中，Aij是|A|的元素aij的代数余子式（i，j=1，2，…
【主要内容】
1.伴随矩阵
设A是n阶矩阵，则称
为A的伴随矩阵，其中，Aij是|A|的元素aij的代数余子式（i，j=1，2，…，n）.
伴随矩阵的性质：设A，B都是n阶矩阵，则
（1）A∗A=AA∗=|A|En；
（2）|A∗|=|A|n-1（n>1）；
（3）（λA）∗=λn-1A∗（其中，λ是常数）；
（4）（AT）∗=（A∗）T；
（5）（AB）∗=B∗A∗；
（6）设M1，M2都是方阵，则
2.矩阵求逆运算
设A是n阶矩阵，如果存在n阶矩阵B，使得AB=BA=En，则称A是可逆矩阵（简称A可逆），B是A的逆矩阵.由于A的逆矩阵是唯一的，记为A-1.由矩阵A产生矩阵A-1的运算，称为矩阵的求逆运算，简称求逆.
可逆矩阵的性质：设A，B都是n阶矩阵，则
（1）A可逆的充分必要条件为|A|≠0.
（2）如果A可逆，则A-1也可逆，且（A-1）-1=A.
（3）如果A可逆，常数λ≠0，则λA可逆，且
（4）如果A，B都可逆，则AB可逆，且（AB）-1=B-1A-1.
（5）如果A可逆，则AT可逆，且（AT）-1=（A-1）T.
（6）如果A可逆，则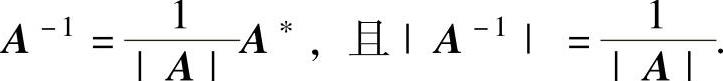
（7）如果A可逆，则A↔En.
（8）如果A可逆，则A∗可逆且（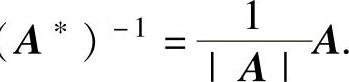
（9）当M1，M2可逆时有
（10）初等矩阵是可逆矩阵，且
[En（i，j（k））]-1=En（i，j（-k）），[En（i（k），j）]-1=En（i（-k），j）.
3.求逆方法
（1）伴随矩阵法
设A是可逆矩阵，则
（2）初等变换法
设A是n阶矩阵，如果对矩阵（A︙En）施行一系列初等行变换成为（En︙B），则A-1=B.
【典型例题】
例5.5.1 设A是n阶矩阵，a是非零常数.记B是A的第i行的每个元素都乘以a后的矩阵，试用A∗表示B∗.
精解 利用伴随矩阵性质求解.
由题设知 B=En（i（a））A，所以
即B∗是矩阵A∗的除第i列外，每个元素都乘以a的矩阵.
例5.5.2 （单项选择题）设矩阵
其中，A可逆，则B-1=（ ）.(www.chuimin.cn)
A.A-1P1P2 B.P1A-1P2 C.P1P2A-1 D.P2A-1P1
精解 互换A的第2列与第3列后再互换第1列与第4列得到B，所以B=AP2P1，从而由可逆矩阵性质得
B-1=（AP2P1）-1=P1-1P2-1A-1=P1P2A-1.
因此本题选C.
例5.5.3 （单项选择题）设A是n（n≥2）阶可逆矩阵，交换A的第1行与第2行得到矩阵B，且A∗，B∗分别为A，B的伴随矩阵，则（ ）.
A.交换A∗的第1、2列得到B∗
B.交换A∗的第1、2行得到B∗
C.交换A∗的第1、2列得到-B∗
D.交换A∗的第1、2行得到-B∗
精解 通过确定B∗的关于A∗的表达式得到正确的选项.
由 B=En（1，2）A 得
B∗=[En（1，2）A]∗=A∗[En（1，2）]∗=A∗·|En（1，2）|[En（1，2）]-1
=A∗·（-1）En（1，2）（由于|En（1，2）|=-1，[En（1，2）]-1=En（1，2））
=-A∗En（1，2），
即A∗En（1，2）=-B∗，
因此本题选C.
例5.5.4 设四阶矩阵
求[（E4-C-1B）TCT]-1.
精解 先利用转置矩阵与可逆矩阵的有关性质化简矩阵式（E4-C-1B）TCT，然后再计算它的逆矩阵.由于
所以
可以利用初等变换法计算上述矩阵的逆矩阵：由于
所以，
例5.5.5 设三阶矩阵
，求行列式
的值，其中，A∗是
A的伴随矩阵.
精解 先化简矩阵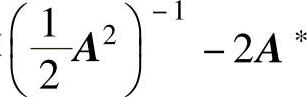
，然后计算它的行列式.
容易算出|A|=2.由于
所以，
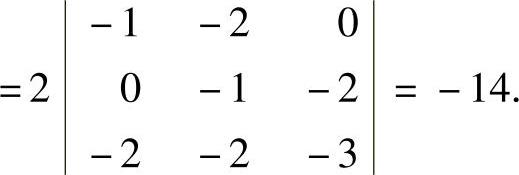
例5.5.6 已知n阶矩阵A=（aij），B=（bij）都可逆，且
证明：矩阵B-En可逆，并求（B-En）-1.
精解 只要证明存在n阶矩阵C，使得C（B-En）=En即可.
由题设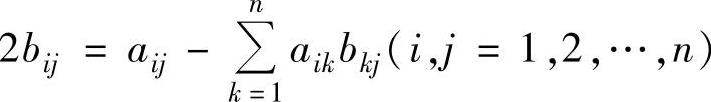
得2B=A-AB，即2（B-En）+A（B-En）=-2En.
由此得到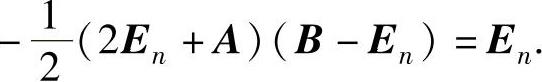
因此B-En可逆，且
注 当M是n阶矩阵时，欲证其可逆，只要证明存在矩阵P使
PM=En或MP=En即可.
有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章
- 详细阅读
-
线性代数9讲-实对称矩阵与正交矩阵详细阅读
（1）若A为实对称矩阵，则①特征值均为实数，特征向量均为实向量.②不同特征值对应的特征向量正交.（即λ1≠λ2ξ1⊥ξ2（ξ1，ξ2）＝0，建方程）③可用正交矩阵相似对角化.（即存在正交矩阵P，使P－1AP＝PTAP＝Λ）见例8.12至例8.15.（2）若A为正交矩阵，则ATA＝EA－1＝ATA由规范正交基组成AT是正交矩阵A－1是正交矩阵A*是正交矩阵－A是正交矩阵.（3）若A，B为同阶正交矩阵......
2023-11-21
-
矩阵运算与分块矩阵简明指南详细阅读
，n）排成的m行n列的矩形表称为m×n矩阵，aij称为A的第i行第j列的元素（i=1，2，…，As都是方阵），则，|A|=|A1||A2|…，n.于是将式代入式得|A+B|=2n-1，即21-n|A+B|=|A|+|B|.例5.3.3 设n阶矩阵A，B，C满足AB=BC=CA=En，求A2+B2+C2.精解 由AB=BC=CA=En得A2=AEnA=AA==E2n=En，B2=BEnB=BB==E2n=En，C2=CEnC=CC==E2n=En，所以，A2+B2+C2=En+En+En=3En.例5.3.4 设n阶矩阵A，B满足ATA=AAT=En，BTB=BBT=En，且|A|=-|B|，证明：|A+B|=0.精解 由题设知，|A+B|=|EnA+BEn|=|BBTA+BATA|=|B||BT+AT||A|=-|A|2|（A+B）T|=-|A|2|A+B|，即|A+B|=0.由此推出|A+B|=0.......
2023-10-27
-
专业能力素质达成矩阵设计与应用详细阅读
课程体系建立后，需要对各门课程的能力素质达成情况进行考查。将课程i的j目标的达成度记为Ti，j，则该课程对专业能力素质培养的总达成度为所有课程对第j项能力素质目标的总达成度为式中，K为开设课程的数量。专业能力素质达成度Q表示为或表示为上述两式具有不同的含义。专业开设的课程和能力素质目标共同构成了专业能力素质达成矩阵，即表3-1所示为其表格形式。......
2023-06-15
-
坐标变换与变换矩阵详细阅读
坐标变换的思路是，将交流电动机的物理模型等效地变换成类似直流电动机的模式，这样分析和控制就可以大大简化。利用坐标变换就可以求出iA、iB、iC与iα、iβ和im、it之间准确的等效关系。图2-4 旋转的直流绕组按照所采用的条件，电流变换矩阵也就是电压变换矩阵，也是磁链的变换矩阵。由图可见iα、iβ和im、it之间存在关系如式，C2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。......
2023-06-19
-
矩阵相似定义及性质概述详细阅读
1.矩阵相似的定义设A，B都是n阶矩阵.如果存在n阶可逆矩阵P，使得B=P-1AP，则称矩阵A与B相似，也称A与B为相似矩阵，记为A～B.2.矩阵相似的性质设A，B，C都是n阶矩阵，则有以下性质：A～A.如果A～B，则B～A.如果A～B，B～C，则A～C.如果A～B，则AT～BT，Am～Bm，λA～λB，φ～φ（其中，φ（λ）=a0+a1λ+…......
2023-10-27
-
节点导纳矩阵的形成与修改详细阅读
用节电导纳矩阵描述的节点电压方程是依靠节点导纳矩阵来建立节点电流与节点电压之间关系的，因此须先确定节点导纳矩阵。在复杂电力网中，这种情况较多，从而使矩阵中出现大量的零元素，节点导纳矩阵成为稀疏矩阵。因此，节点导纳矩阵是一个对称、稀疏且具有对角线优势的方阵。......
2023-06-15
-
矩阵方程AX=B的求解方法详细阅读
【主要内容】设A是m×n矩阵，B是m×l矩阵，它们都是已知矩阵，X是未知矩阵，则称方程AX=B为矩阵方程.满足AX=B的矩阵X称为该方程的解.设A=（A┆B），称为该矩阵方程的增广矩阵，则AX=B有唯一解的充分必要条件是，AX=B有无穷多解的充分必要条件是，AX=B无解的充分必要条件是注 （ⅰ）矩阵方程AX=O（其中，A是已知的m×n矩阵，O是m×l零矩阵）有非零解的充分必要条件是r（A）
2023-10-27
相关推荐