给出向量组（Ⅰ）：α1，α2，…，αs 线性表示，则称（Ⅰ）与（Ⅱ）等价.其等价的充要条件是r（Ⅰ）＝r（Ⅱ）＝r（Ⅰ，Ⅱ）.向量组等价和矩阵等价是两个不同的概念.矩阵等价要同型，当然行数、列数都要相等；向量组等价要同维，但向量个数可以不等.A，B同型时，ABr＝rPAQ＝B.αi，βj（i＝1，2，…，βt 这两个向量组中的某一个向量组可由另一个向量组线性表出r（α1，α2，…......
2023-11-21
矩阵初等变换、初等矩阵与等价矩阵解析
【摘要】：【主要内容】1.矩阵的初等变换矩阵的下列三种变换称为矩阵的初等行（列）变换：（1）互换矩阵的两行（两列）.（2）用一个非零常数c乘矩阵的某行（某列），即用c乘某行（某列）的每个元素.（3）矩阵某行（某列）的k倍加到另一行（另一列），即某行（某列）的每个元素的k倍，加到另一行（另一列）的对应元素.矩阵的初等行变换与初等列变换，总称矩阵的初等变换.2.初等矩阵单位矩阵经过一次初等变换所得到的矩阵，称为
【主要内容】
1.矩阵的初等变换
矩阵的下列三种变换称为矩阵的初等行（列）变换：
（1）互换矩阵的两行（两列）.
（2）用一个非零常数c乘矩阵的某行（某列），即用c乘某行（某列）的每个元素.
（3）矩阵某行（某列）的k倍加到另一行（另一列），即某行（某列）的每个元素的k倍，加到另一行（另一列）的对应元素.
矩阵的初等行变换与初等列变换，总称矩阵的初等变换.
2.初等矩阵
单位矩阵经过一次初等变换所得到的矩阵，称为初等矩阵.n阶初等矩阵有以下三类：
（1）
第i列 第j列（互换En的第i行（第i列）与第j行（第j列）后所得的n阶矩阵）.
（2）
第i列（非零常数c乘En的第i行（第i列）后所得的n阶矩阵）.
（3）
第i列 第j列（En的第j行的k倍加到第i行，或第i列的k倍加到第j列所得到的n阶矩阵）.
注 （ⅰ）矩阵A的一次初等行（列）变换所得的矩阵等于A左（右）乘一个相应的初等矩阵.例如互换m×n矩阵A的第i行（列）与第j行（列）后的矩阵为B，则
B=Em（i，j）A（B=AEn（i，j））；
（ⅱ）[En（i，j（k））]T=En（j，i（k）），[En（i（k），j）]T=En（j（k），i）.
3.矩阵等价
设矩阵B是矩阵A经过有限次初等变换后得到的矩阵，则称A与B等价，记为A↔B.
设A，B，C都是m×n矩阵，则(www.chuimin.cn)
（1）A↔A.
（2）设A↔B，则B↔A.
（3）设A↔B，B↔C，则A↔C.
（4）设A↔B，则A等于B与若干个初等矩阵之积.
【典型例题】
例5.4.1 （单项选择题）设A是三阶矩阵，将A的第1列与第2列互换得矩阵B，再将B的第2列加到第3列得C，则满足AQ=C的矩阵Q=（ ）.
精解 Q应是题中所给的两个初等列变换所对应的初等矩阵之积，即
因此本题选D.
例5.4.2 设矩阵
，求矩阵PAQ
及APQ.
精解 P和Q都是三阶初等矩阵，所以可由初等变换直接算出PAQ及APQ.
PAQ是对A进行初等行变换（互换第1行与第2行）后，再进行初等列变换（将第3列的2倍加到第1列）而成的矩阵，所以
因此
APQ是对A进行初等列变换（互换第1列与第2列）后，再进行初等列变换（将第3列的2倍加到第1列）而成的矩阵，所以
因此
例5.4.3 设矩阵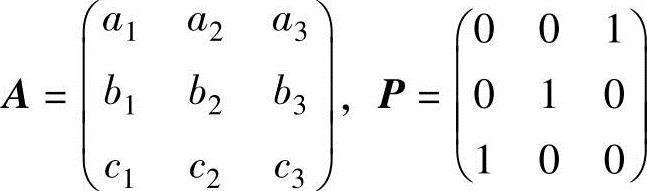
，求P10APm（其中，m是正整数）.
精解 P是初等矩阵，P10A即为对A施行10次互换第1行与第3行的初等行变换而成的矩阵，所以
P10A=A.因此，P10APm=APm是对A施行m次互换第1列与第3列的初等列变换而成的矩阵，所以，当m为正偶数时，APm=A；当m为正奇数时，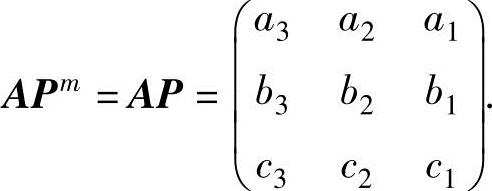
从而
有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章
- 详细阅读
-
矩阵初等变换及相抵定理原理介绍详细阅读
初等变换对于矩阵来说是最重要的运算.初等变换到底改变了什么呢？，Ps，Q1，Q2，…，Qt，满足条件P=P1P2…Qt.因此，我们可以得到关系式P1P2…Qt=B. 由命题3.2得到，式就表明，矩阵A可以通过一系列的行与列的初等变换化为矩阵B.证毕.定理3.4m×n阶矩阵A必可相抵于一个形如的矩阵，该矩阵中除了a11，a22，…......
2023-11-22
-
高等代数：矩阵初等变换的操作方法详细阅读
，Ps，使得对所得矩阵再进行列的初等变换，变为即存在一些初等方阵Q1，Q2，…P2P1E=A-1.由于在矩阵的左边乘上一个初等方阵P，相当于对这个矩阵作一个与P相对应的初等行变换.上面两个等式表明，对A依次作P1，P2，…......
2023-11-22
- 详细阅读
-
线性代数9讲-实对称矩阵与正交矩阵详细阅读
（1）若A为实对称矩阵，则①特征值均为实数，特征向量均为实向量.②不同特征值对应的特征向量正交.（即λ1≠λ2ξ1⊥ξ2（ξ1，ξ2）＝0，建方程）③可用正交矩阵相似对角化.（即存在正交矩阵P，使P－1AP＝PTAP＝Λ）见例8.12至例8.15.（2）若A为正交矩阵，则ATA＝EA－1＝ATA由规范正交基组成AT是正交矩阵A－1是正交矩阵A*是正交矩阵－A是正交矩阵.（3）若A，B为同阶正交矩阵......
2023-11-21
-
矩阵运算与分块矩阵简明指南详细阅读
，n）排成的m行n列的矩形表称为m×n矩阵，aij称为A的第i行第j列的元素（i=1，2，…，As都是方阵），则，|A|=|A1||A2|…，n.于是将式代入式得|A+B|=2n-1，即21-n|A+B|=|A|+|B|.例5.3.3 设n阶矩阵A，B，C满足AB=BC=CA=En，求A2+B2+C2.精解 由AB=BC=CA=En得A2=AEnA=AA==E2n=En，B2=BEnB=BB==E2n=En，C2=CEnC=CC==E2n=En，所以，A2+B2+C2=En+En+En=3En.例5.3.4 设n阶矩阵A，B满足ATA=AAT=En，BTB=BBT=En，且|A|=-|B|，证明：|A+B|=0.精解 由题设知，|A+B|=|EnA+BEn|=|BBTA+BATA|=|B||BT+AT||A|=-|A|2|（A+B）T|=-|A|2|A+B|，即|A+B|=0.由此推出|A+B|=0.......
2023-10-27
-
向量组的标准正交化与正交矩阵解析详细阅读
+anbn=0时，称α与β正交.2.向量组的单位正交化单位正交向量组设α1，α2，…，αm单位正交化的施密特方法如下：（ⅰ）正交化：取β1=α1，（ⅱ）单位化：由此得到的ε1，ε2，…......
2023-10-27
-
初等矩阵定义及特点-张宇线性代数9讲详细阅读
（1）定义（Eij，Eij（k），Ei（k））.①初等变换.（ⅰ）一个非零常数乘矩阵的某一行（列）.（ⅱ）互换矩阵中某两行（列）的位置.（ⅲ）将矩阵的某一行（列）的k倍加到另一行（列）.以上三种变换称为矩阵的初等行（列）变换，且分别称为倍乘、互换、倍加初等行（列）变换.②初等矩阵.由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵.以3阶矩阵为例，并随之给出定义.（ⅰ）E2（k）＝，E 的第2行（或......
2023-11-21
相关推荐