首页理论教育n阶行列式展开规则及解析

n阶行列式展开规则及解析

2023-10-27 理论教育版权反馈

【摘要】：设n阶行列式则有Dn=ai1Ai1+ai2Ai2+…+anjAnj（Dn按第j列展开，j=1，2，…，n），其中，Aij是元素aij的代数余子式，即（-1）i+j与Dn中去掉第i行和第j列元素后的n-1阶行列式之积.注ak1Ai1+ak2Ai2+…，n，但k≠i），a1kA1j+a2kA2j+…

【主要内容】

设n阶行列式

则有

D_n=a_i1A_i1+a_i2A_i2+…+a_inA_in（D_n按第i行展开，i=1，2，…，n）

=a_1jA_1j+a_2jA_2j+…+a_njA_nj（D_n按第j列展开，j=1，2，…，n），其中，A_ij是元素a_ij的代数余子式，即（-1）i+j与D_n中去掉第i行和第j列元素后的n-1阶行列式之积.

注a_k1A_i1+a_k2A_i2+…+a_knA_in=0（i=1，2，…，n，k=1，2，…，n，但k≠i），

a_1kA_1j+a_2kA_2j+…+a_nkA_nj=0（j=1，2，…，n，k=1，2，…，n，但k≠j）.

【典型例题】

例5.2.1 判断

是多少次多项式.

精解利用行列式性质使某行有三个元素为零，然后按该行展开即可确定f（x）的次数.

由此可知f（x）是二次多项式.

例5.2.2 设5阶行列式

，分别求A₂₁+A₂₂+A₂₃与A₂₄+A₂₅的值，

其中，A_2j是D₅的元素a_2j的代数余子式（j=1，2，3，4，5）.

精解 A₂₁，A₂₂，A₂₃，A₂₄，A₂₅是D5的第二行各个元素的代数余子式.为了计算A₂₁+A₂₂+A₂₃与A₂₄+A₂₅的值，需要将行列式按第1行与第3行展开并构造以它们为未知数的方程组：

即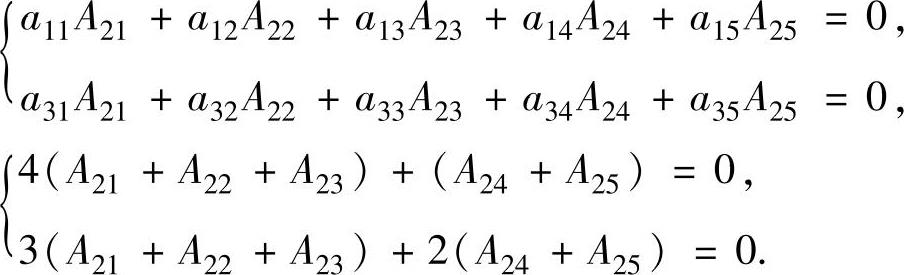(www.chuimin.cn)

解此方程组得

A₂₁+A₂₂+A₂₃=0，A₂₄+A₂₅=0.

例5.2.3 求n阶行列式

精解将D_n按第1列展开

（n-1）阶（n-1）阶

=a·a^n-1+（-1）ⁿ⁺¹b·b^n-1=aⁿ+（-1）ⁿ⁺¹bⁿ.

例5.2.4 求n阶行列式

精解根据D₁，D₂，D₃，…推出D_n的表达式，然后用数学归纳法证明这个表达式是正确的.

由D_n的定义知

=4a³，依次类推可得

D_n=（n+1）aⁿ.（1）

下面用数学归纳法证明式（1）是正确的.

显然式（1）对n=1，2，3都是成立的.设式（1）对小于n的情形都成立，例如，D_n-2=（n-1）a^n-2，D_n-1=na^n-1，则

（n-2）阶

=2aD_n-1-a²D_n-2=2a·na^n-1-a²（n-1）a^n-2（这里利用了归纳法中的假设）=（n+1）aⁿ.

由此证得，对n=1，2，…式（1）都成立.