回答是肯定的,下面更深入地讨论这个问题.......
2023-10-30
【主要内容】
1.求幂级数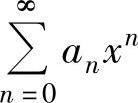 和函数的方法
和函数的方法 的和函数可按以下方法计算:
的和函数可按以下方法计算:
(1)对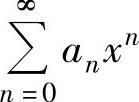 进行适当的代数运算(例如,将
进行适当的代数运算(例如,将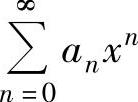 的各项同乘以一个常数或xk,或者
的各项同乘以一个常数或xk,或者
提出一个常数或xk,k为某个正整数),或作适当的变量代换,使其成为常用函数的麦克劳林级
数,从而求得 的和函数s(x).有时将
的和函数s(x).有时将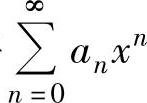 表示成几个幂级数之和,然后对每个幂级
表示成几个幂级数之和,然后对每个幂级
数都作以上处理,由此算得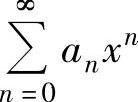 的和函数s(x).
的和函数s(x).
(2)对 在收敛区间内进行求导或积分运算,使其成为某个常用函数的麦克劳林级
在收敛区间内进行求导或积分运算,使其成为某个常用函数的麦克劳林级
数或几个常用函数的麦克劳林级数之和,由此求得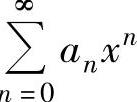 的和函数s(x).
的和函数s(x).
2.求幂级数 和函数的方法
和函数的方法
令y=x-x0,所给幂级数成为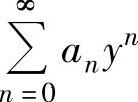 ,利用上一段所述方法算出它的和函数,记为
,利用上一段所述方法算出它的和函数,记为
s1(y),则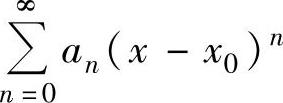 的和函数s(x)=s1(x-x0).
的和函数s(x)=s1(x-x0).
【典型例题】
例4.14.1 求幂级数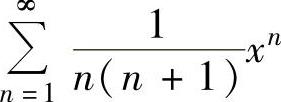 的和函数s(x).
的和函数s(x).
精解 所给幂级数的收敛域为[-1,1],对任意x∈[-1,1)有 ,(1)
,(1)
其中,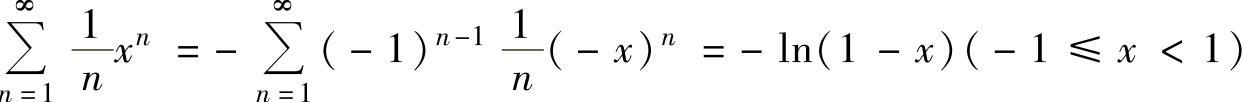 ,
,
将它们代入式(1)得
即当x∈[-1,0)∪(0,1)时,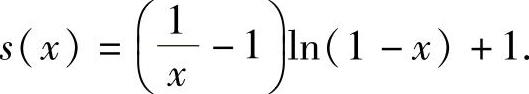
此外,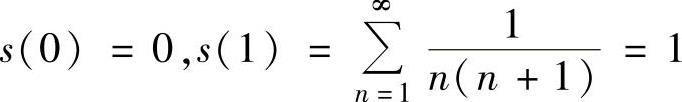 ,
,
综上所述,
例4.14.2求幂级数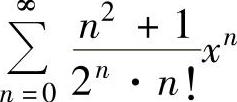 的收敛域与和函数.
的收敛域与和函数.
精解 由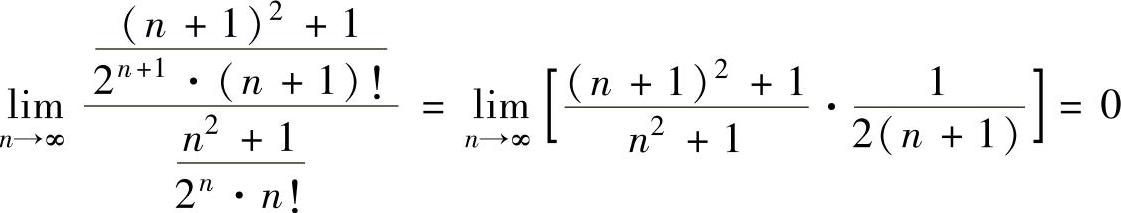 知,所给幂级数的
知,所给幂级数的
收敛半径R=+∞,由此得收敛域为(-∞,+∞).对任意x∈(-∞,+∞)有
例4.14.3 求幂级数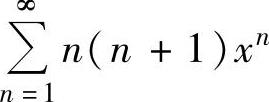 的和函数s(x).(www.chuimin.cn)
的和函数s(x).(www.chuimin.cn)
精解 记 的和函数为s1(x),则s(x)=xs1(x).(1)
的和函数为s1(x),则s(x)=xs1(x).(1)
由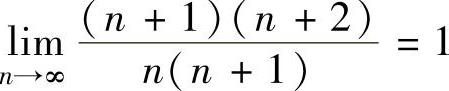 知
知 的收敛半径为R=1,收敛区间为(-1,1),
的收敛半径为R=1,收敛区间为(-1,1),
并且x=-1,1都不是收敛点,所以收敛域为(-1,1),即 ,
,
于是
式(2)的两边在(-1,1)内积分得
式(3)两边对x求二阶导数得
代入式(1)得
注 由以上三个例题可知,当幂级数 的系数如
的系数如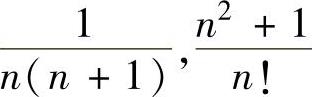 等是关于n的有
等是关于n的有
理分式时,通常用逐项求导求和函数;当幂级数 的系数如n(n+1)等是关于n的整式
的系数如n(n+1)等是关于n的整式
时,通常用逐项积分求和函数.
例4.14.4 求幂级数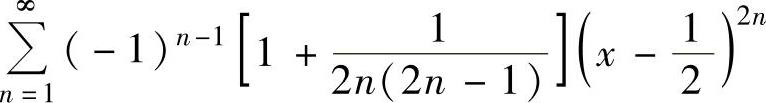 的收敛域与和函数s(x).
的收敛域与和函数s(x).
精解 显然,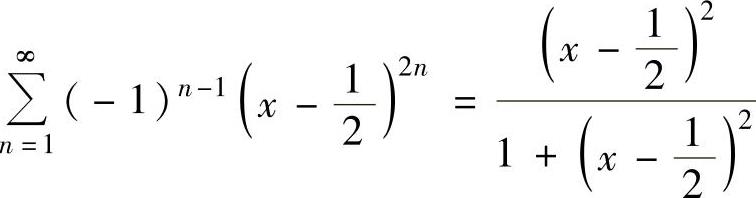 ,它的成立范围为
,它的成立范围为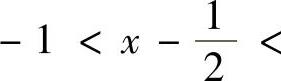
1,即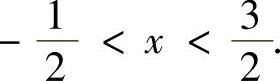
下面计算
的收敛域与和函数s1(x).
由于式(1)是缺项幂级数,所以利用正项级数比较判别法计算它的收敛域:
由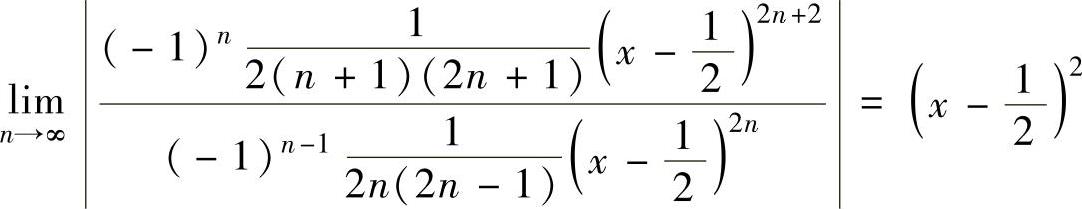 知,在
知,在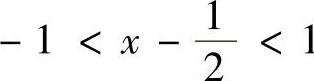 ,即
,即 时,
时,
成立,因此,题中所给幂级数的收敛域为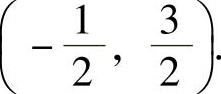
在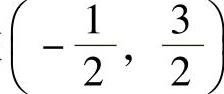 内,式(2)两边对x分别求两次导数得
内,式(2)两边对x分别求两次导数得
对于任意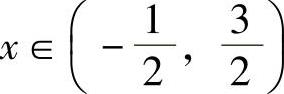 ,式(3)积分得
,式(3)积分得
对于任意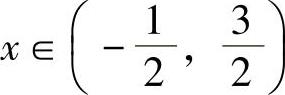 ,式(4)积分得
,式(4)积分得
综上所述,对 有
有
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

;写出幂级数,并求出收敛半径R;考查当x在区间内时余项Rn的极限是否为零.如果为零,则函数f在区间内的幂级数展开式为例1 将函数f=ex展开成x的幂级数.解 由fn=ex,得fn=1(n=0,1,2,…......
2023-10-19

【主要内容】1.函数展开成幂级数的概念设函数f(x)在点x0的某个邻域内有定义.如果存在幂级数,使得这个邻域内的任意x都有,则称f(x)在点x0处能展开成幂级数,或称f(x)能展开成关于x-x0的幂级数.如果f(x)在点x0处的某个邻域内具有任意阶导数,则称幂级数为f(x)在点x0处的泰勒级数.特别地,称f(x)在点x=0处的泰勒级数为f(x)的麦克劳林级数.如果f(x)在点x0能展开成幂级数,则......
2023-10-27

对于收敛圆的圆心相同的两个复数项幂级数,它们的四则运算可以像实数项幂级数那样来进行,要根据其系数来确定.对于和、差、积所得幂级数在其公共收敛圆内显然收敛,其收敛半径不会小于所给级数的收敛半径最小的一个.如对乘积运算若上式左端两个幂级数的收敛半径分别为R1和R2,则其积的幂级数收敛半径R >min{R1,R2}.为了说明两个幂级数经过运算后所得的幂级数的收敛半径确实可以大于R1 和R2 中较小的一个......
2023-10-30

解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30

试述调和函数的定义、特性及应用。调和函数的意义。调和函数的特性。工程数学或高等数学发现,如果一个函数u(x,y)为调和函数,则该函数具备“可迭加”的特性。证明如果流体为x-y平面理想流体,流体在流动时的流线函数φ为调和函数,则函数具有迭加性。......
2023-06-29

前面我们介绍了等值比较函数“=”,它只能用于数、符号原子和字符串,即原子的等值比较函数,它不能用于表。eq函数用于检查两个表达式<expr1>和<expr2>是否约束于同一对象,即它们不仅值相等,而且占用同一内存单元。因此,任选变元<fuzz>可以让用户指定表达式<expr1>和<expr2>间的最大差值,在此范围内,仍然认为<expr1>和<expr2>是相等的。所有同源值一定相等不同源时,INTREALSTR类型一定相等不同源时,ENAME类型,“=”不等,“eqequal”相等。......
2023-11-02
相关推荐