回答是肯定的,下面更深入地讨论这个问题.......
2023-10-30
【主要内容】
1.函数展开成幂级数的概念设函数f(x)在点x0的某个邻域内有定义.如果存在幂级数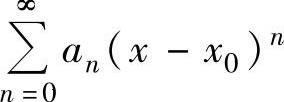 ,使得这个邻
,使得这个邻
域内的任意x都有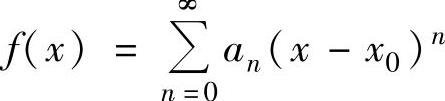 ,
,
则称f(x)在点x0处能展开成幂级数,或称f(x)能展开成关于x-x0的幂级数.
如果f(x)在点x0处的某个邻域内具有任意阶导数,则称幂级数
为f(x)在点x0处的泰勒级数.特别地,称f(x)在点x=0处的泰勒级数
为f(x)的麦克劳林级数.
如果f(x)在点x0能展开成幂级数,则这个幂级数必为f(x)在点x0处的泰勒级数,此时对点x0的某个邻域内的任意x有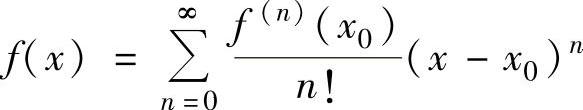 ,
,
称这一表达式为f(x)在点x0处的泰勒展开式.特别地,称f(x)在点x=0处的泰勒展开式
为f(x)的麦克劳林展开式.
2.函数能展开成泰勒级数的充分必要条件
设函数f(x)在点x0的某个邻域内具有任意阶导数,则f(x)在点x0处能展开成泰勒级数,即在点x0的某个邻域内有
的充分必要条件是对上述邻域内的任意x都有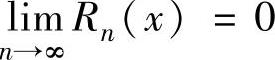 ,其中
,其中 (ξn是介于x0与x之间的实数,且与n有关),
(ξn是介于x0与x之间的实数,且与n有关),
即f(x)在点x0处的n阶泰勒公式的拉格朗日型余项.
3.常用函数的麦克劳林展开式
(1) ,
,
(2) ,
,
(3)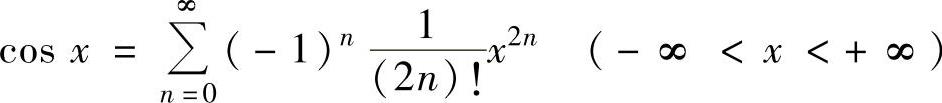 ,
,
(4)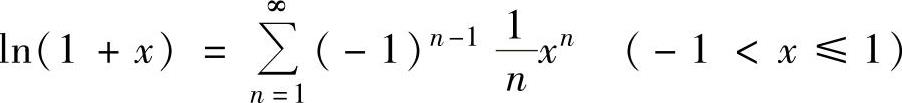 ,
,
(5)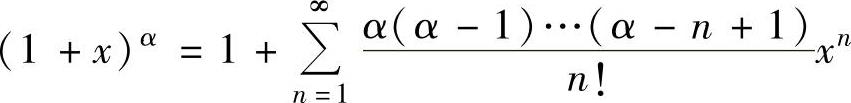 (当α≤-1,-1<α<0及α>0时,
(当α≤-1,-1<α<0及α>0时,
展开式的成立范围分别为-1<x<1,-1<x≤1,-1≤x≤1),
特别地, ,
,
4.函数展开成幂级数的方法
通常采用间接法,将函数展开成幂级数.
(1)将f(x)展开成关于x的幂级数
要将f(x)展开成关于x的幂级数,可以将f(x)表示成常用函数ex,sinx,cosx,ln(1+x),(1+x)α或它们的线性组合(注意:这里的线性组合中的系数可以是常数,也可以是x的正整数次幂),或通过变量代换与对f(x)进行求导、积分等运算使它成为常用函数ex,sinx,cosx,ln(1+x),(1+x)α或它们的线性组合,然后利用常用函数的麦克劳林展开式以及幂级数在收敛区间内的基本性质,将f(x)展开成关于x的幂级数.
(2)将f(x)展开成关于x-x0的幂级数
令t=x-x0,记φ(t)=f(t+x0),将φ(t)按(1)中所述方法展开成关于t的幂级数, ,
,
于是f(x)的幂级数展开式为
注 幂级数在收敛区间内的基本性质:
设幂级数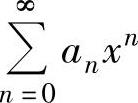 的收敛半径为R,其和函数为s(x),即
的收敛半径为R,其和函数为s(x),即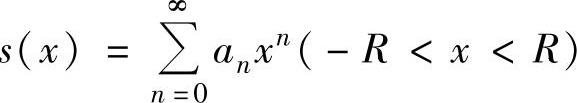 ,
,
则
(ⅰ)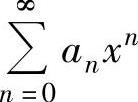 在收敛区间内绝对收敛,s(x)在收敛域上连续,在收敛区间内可导.
在收敛区间内绝对收敛,s(x)在收敛域上连续,在收敛区间内可导.
(ⅱ)对x∈(-R,R)有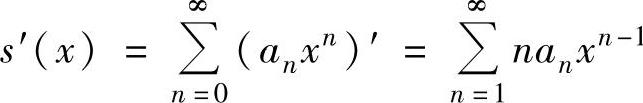 (即在收敛区间内,幂级数可逐项求导),
(即在收敛区间内,幂级数可逐项求导),
上式右边的幂级数的收敛半径仍为R,但它的收敛域与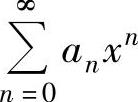 的收敛域未必相同,即当x=
的收敛域未必相同,即当x=
R是 的收敛点时,未必也是
的收敛点时,未必也是 的收敛点,需具体检验;对点x=-R也有同样的说法.
的收敛点,需具体检验;对点x=-R也有同样的说法.
(ⅲ)对x∈(-R,R)有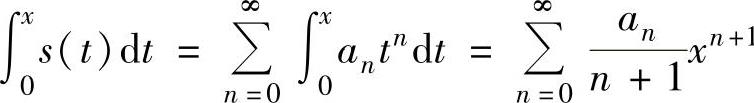 (即在收敛区间内,幂级数可逐项积分),(www.chuimin.cn)
(即在收敛区间内,幂级数可逐项积分),(www.chuimin.cn)
上式左边的幂级数的收敛半径仍为R,但它的收敛域与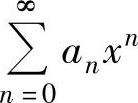 的收敛域未必相同,即当x=
的收敛域未必相同,即当x=
R不是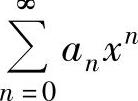 的收敛点时,也可能是
的收敛点时,也可能是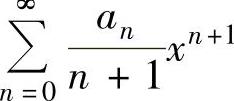 的收敛点,需具体检验;对点x=-R也有同
的收敛点,需具体检验;对点x=-R也有同
样的说法.
【典型例题】
例4.13.1 将下列函数展开成关于x的幂级数:
(1)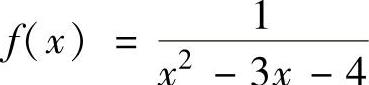 ;
;
(2)
精解 (1)

由于 成立范围为
成立范围为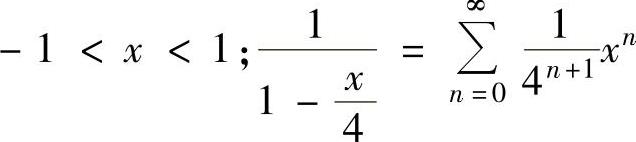 的成立范围为
的成立范围为
-4<x<4,所以式(1)的成立范围为-1<x<1.
(2)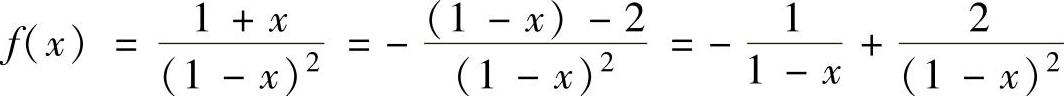 ,(2)
,(2)
其中, ,
,
将它们代入式(2)得
例4.13.2 将下列函数展开成关于x的幂级数:
(1)f(x)=ln(e-x);
(2)f(x)=cos2x.
精解 (1)
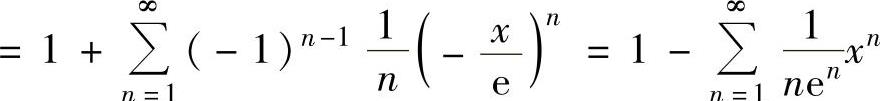 ,
,
上式成立的范围为 ,即-e≤x<e.
,即-e≤x<e.
(2)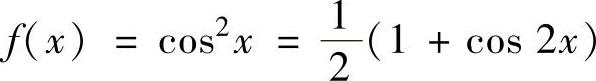
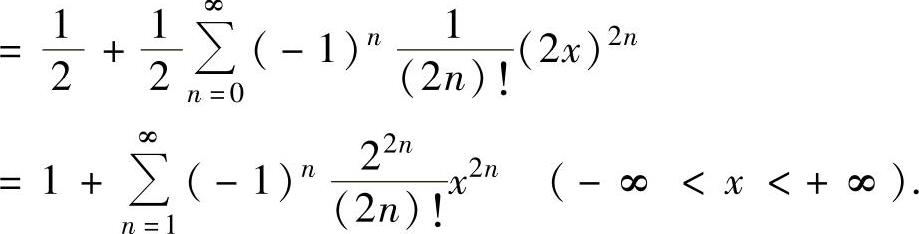
例4.13.3 将下列函数在点x=1处展开成幂级数:
(1)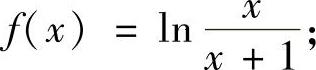
(2)
精解 (1)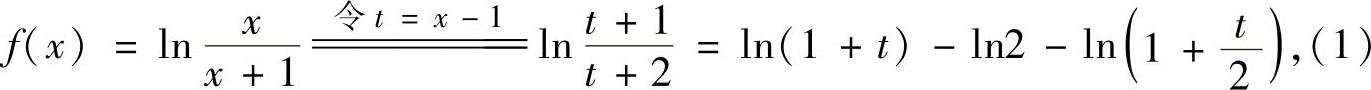
其中,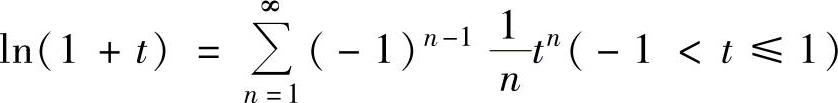 ,
,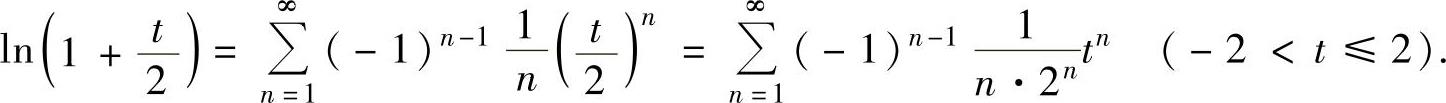
将它们代入式(1)得
(2)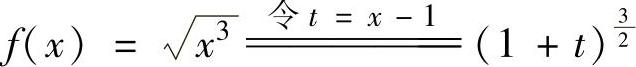
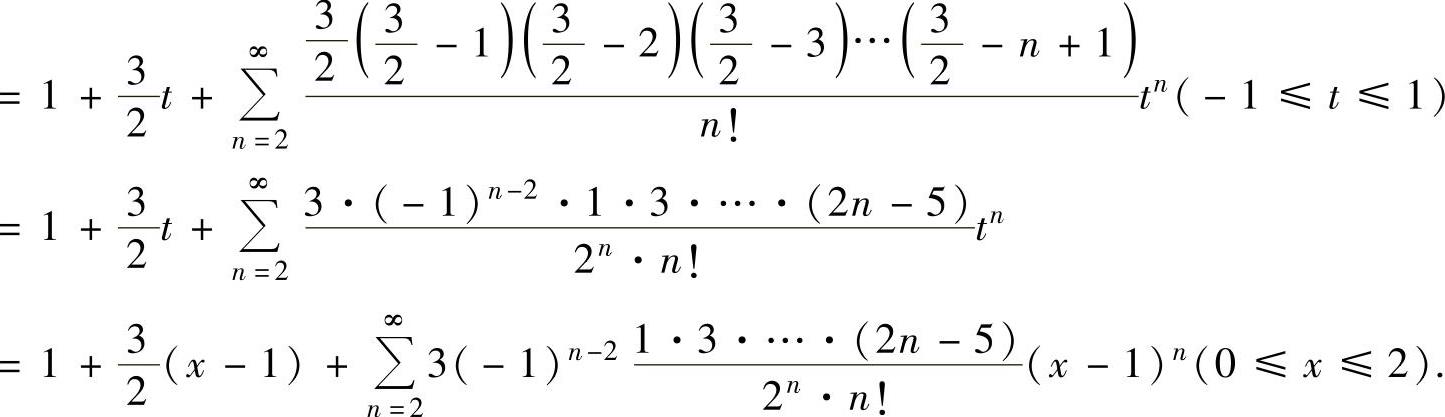
例4.13.4 将下列函数展开成关于x的幂级数:
(1)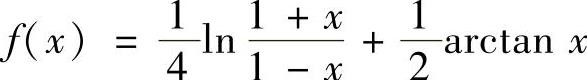 ;
;
(2)
精解 (1)f(x)不是常用函数的线性组合,所以从考虑f′(x)入手将f(x)展开成关于x的幂级数.
所以,
(2)由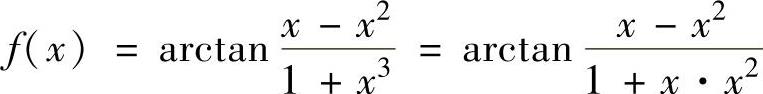

知,只要将arctanx展开成x的幂级数即可得到f(x)的幂级数展开式.由于
所以
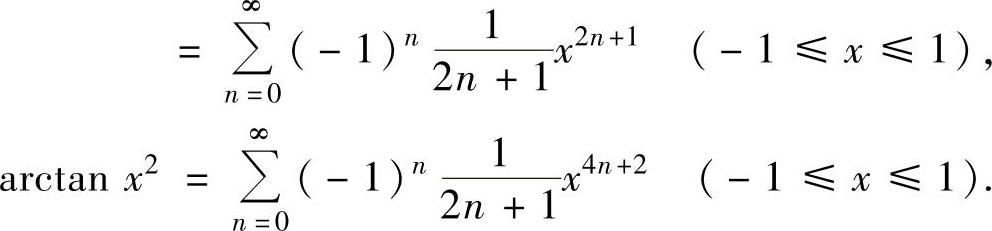
将它们代入式(1)得 ,
,
其中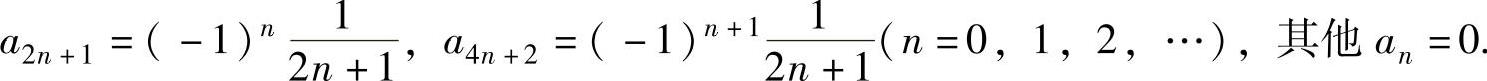
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

【主要内容】1.求幂级数和函数的方法的和函数可按以下方法计算:(1)对进行适当的代数运算(例如,将的各项同乘以一个常数或xk,或者提出一个常数或xk,k为某个正整数),或作适当的变量代换,使其成为常用函数的麦克劳林级数,从而求得的和函数s(x).有时将表示成几个幂级数之和,然后对每个幂级数都作以上处理,由此算得的和函数s(x).(2)对在收敛区间内进行求导或积分运算,使其成为某个常用函数的麦克劳林......
2023-10-27

;写出幂级数,并求出收敛半径R;考查当x在区间内时余项Rn的极限是否为零.如果为零,则函数f在区间内的幂级数展开式为例1 将函数f=ex展开成x的幂级数.解 由fn=ex,得fn=1(n=0,1,2,…......
2023-10-19

请你为剩下的那个图像写出与之相吻合的事件.习题图2-2我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;我骑着车一路匀速行驶,只是在途中遇到了一次交通堵塞,耽搁了一些时间;我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.......
2023-11-22

对于收敛圆的圆心相同的两个复数项幂级数,它们的四则运算可以像实数项幂级数那样来进行,要根据其系数来确定.对于和、差、积所得幂级数在其公共收敛圆内显然收敛,其收敛半径不会小于所给级数的收敛半径最小的一个.如对乘积运算若上式左端两个幂级数的收敛半径分别为R1和R2,则其积的幂级数收敛半径R >min{R1,R2}.为了说明两个幂级数经过运算后所得的幂级数的收敛半径确实可以大于R1 和R2 中较小的一个......
2023-10-30

在第一节中我们知道,复数与平面内的点或向量建立了一一对应关系,所以我们对复数、平面内的点和向量不加区别.除此之外,复数也可与球面上的点一一对应,并用球面上的点来表示,具体做法如下:取一个球面,使之与复平面z相切于原点,球面上的一点S与原点重合,如(图1-5).通过点S作一条垂直于复平面的直线与球面交于另一点N,我们称N为北极,S为南极.对于复平面内任何一点z,现在用直线段将点z与北极N连接起来,那......
2023-10-30

解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30
相关推荐