首页理论教育幂级数的收敛规律及其收敛域

幂级数的收敛规律及其收敛域

2025-09-30 理论教育版权反馈

【摘要】：形如的级数称为关于x的幂级数，a0，a1，…

【主要内容】

形如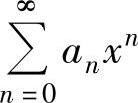的级数称为关于x的幂级数（简称幂级数），a₀，a₁，…，a_n，…称为该幂级数的系数.

幂级数的一般形式为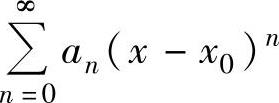，称为关于x-x₀的幂级数.显然，它可令y=x-x0

转换成关于y的幂级数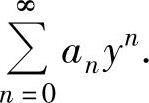因此下面主要讨论关于幂级数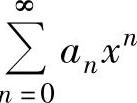的收敛半径、收敛区间

与收敛域.

1.幂级数的收敛半径

设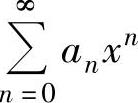，如果它不是仅在点x=0处收敛，也不是对任何实数x都收敛的幂级数，则定

义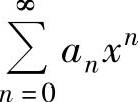的收敛半径为当x<R时该幂级数绝对收敛，当x>R时该幂级数发散的实数

R.

此外，当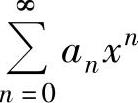仅在点x=0处收敛时，定义它的收敛半径为0；当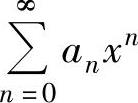对任何实数x

都收敛时，定义它的收敛半径为+∞.

如果幂级数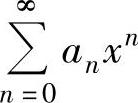有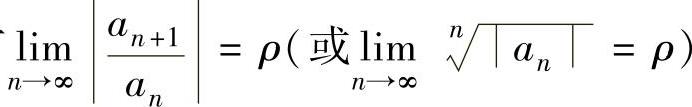，则它的收敛半径为

2.幂级数的收敛区间与收敛域

如果幂级数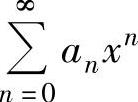的收敛半径R为有限数，则它的收敛区间为（-R，R），收敛域为（-R，R）及其收敛的端点.

如果幂级数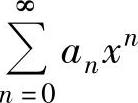的收敛半径R=+∞，则它的收敛区间与收敛域同为（-∞，+∞）；如

果幂级数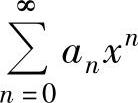的收敛半径R=0，则它没有收敛区间，但收敛域为{0}.

注计算幂级数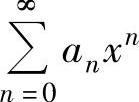的收敛半径、收敛区间与收敛域的前提是数列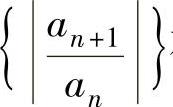存在及

极限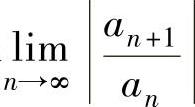存在或为+∞.当这个前提不具备（如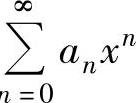是缺项幂级数，即{a_n}中有无

穷多项为零）时，可用正项级数比值判别法或根值判别法确定使正项级数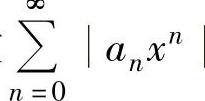收敛的

开区间，例如（-R，R），则R即为收敛半径，至于收敛域则可以由（-R，R）及其收敛的端点确定.

【典型例题】

例4.12.1（单项选择题）设幂级数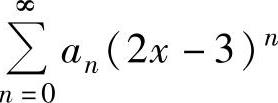在点x=-4处条件收敛，则该幂级数

的收敛半径R为（）.

A.4 B.5 C.8 D.11

精解记y=2x-3，则x=-4时，y=-11.于是由题设知，幂级数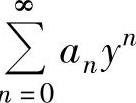在点y=

-11处条件收敛，因此y=-11是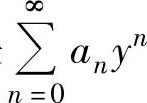收敛域的边界点（这是因为，如果y=-11不是收(https://www.chuimin.cn)

敛域的边界点，则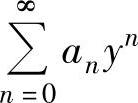在点y=-11处或绝对收敛，或发散，这都与题设矛盾）.从而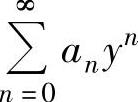，的收敛半径，即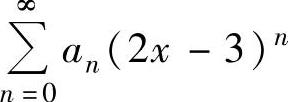的收敛半径R=11.

因此本题选D.

例4.12.2 已知幂级数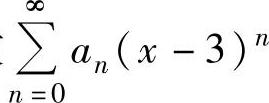在点x=0处收敛，在点x=6处发散，求它的收敛域.

精解令y=x-3，则x=0时，y=-3；x=6时，y=3.于是由题设知幂级数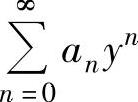

在y=-3处收敛，在y=3处发散，前者可以推出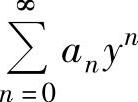的收敛半径R≥3，后者可以推出

R≤3，从而R=3，于是收敛区间为（-3，3），但是y=-3是收敛点，而y=3不是收敛点.因此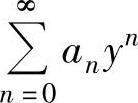的收敛域为[-3，3），由此得到幂级数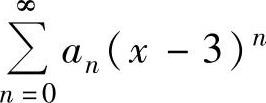的收敛域为[0，6）.

例4.12.3 求幂级数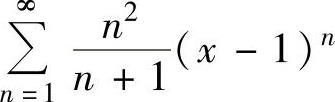的收敛域.

精解记y=x-1，则所给的幂级数成为

由于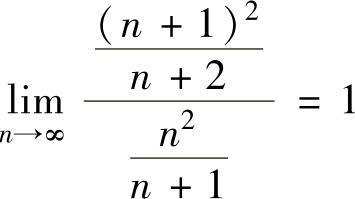，所以式（1）的收敛半径为R=1，收敛区间为（-1，1）.

当y=-1和y=1时，式（1）分别成为，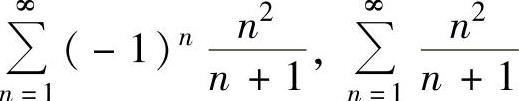

这两个级数的通项极限都不为零，因此它们都是发散的，即y=-1，1都不是式（1）的收敛点.由此可知，式（1）的收敛域为（-1，1），从而所给幂级数的收敛域为（0，2）.

例4.12.4 求下列幂级数的收敛域：

（1）；

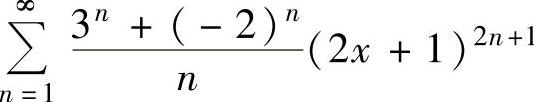（2）

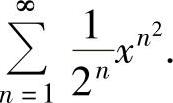
精解（1），（2）中的幂级数都是缺项幂级数，因此要用正项级数比值判别法来计算收敛区间，然后确定收敛域.

（1）记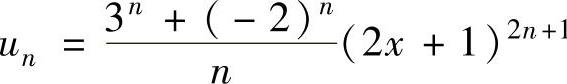，则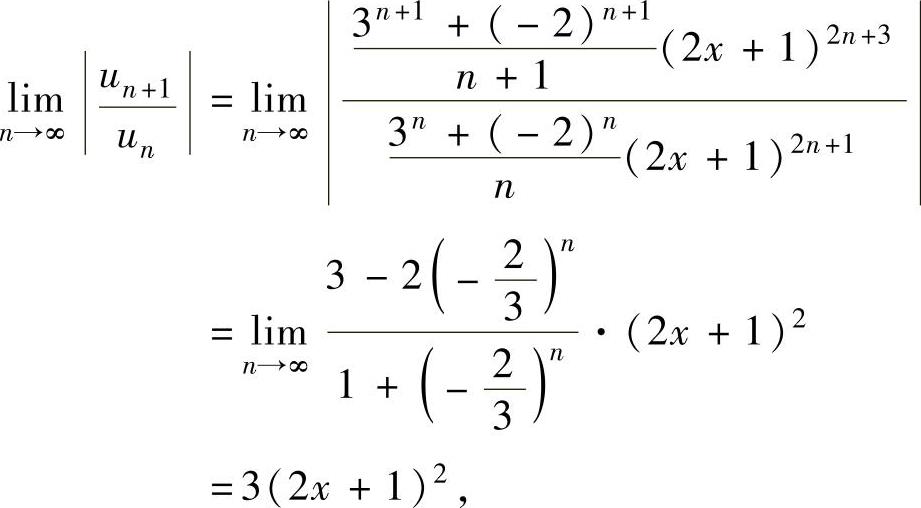

于是，当3（2x+1）2<1，即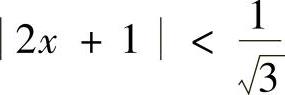时，所给幂级数收敛；当3（2x+1）2>1，即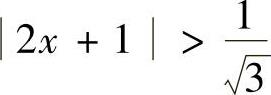时，所给幂级数发散，因此这个幂级数的收敛区间为

下面考虑两个端点，即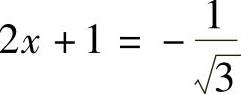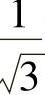，时幂级数的收敛性：

当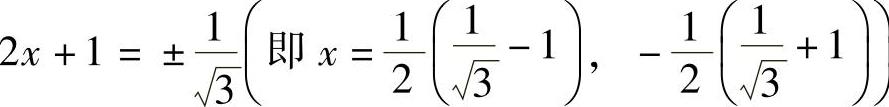时，所给幂级数成为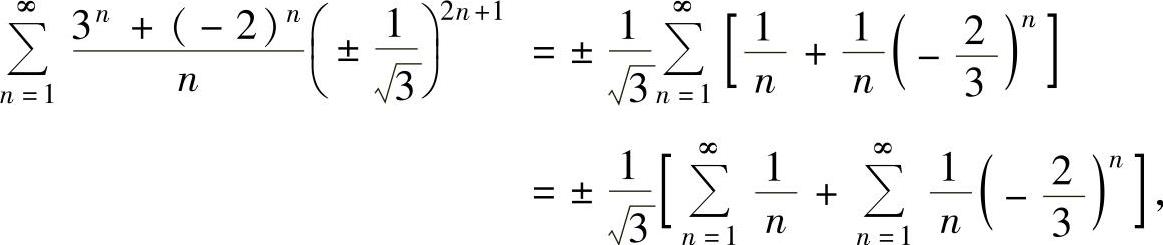

其中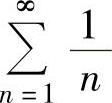，发散，而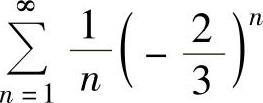绝对收敛，所以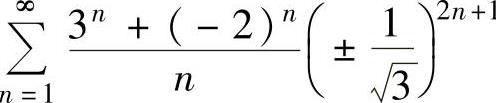发散，即点x=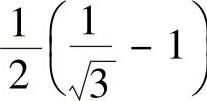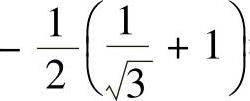，都不是所给幂级数的收敛点.

因此，所给幂级数的收敛域为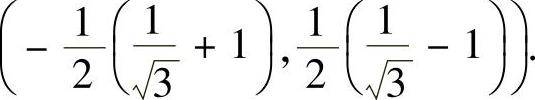

（2）记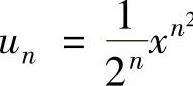，则

所以由正项级数的根值判别法知，当x≤1时，所给幂级数收敛，而x>1时，所给幂级数发散.

从而，这个幂级数的收敛域为{xx≤1}=[-1，1].