首页理论教育2015考研数学任意项级数收敛性判别法

2015考研数学任意项级数收敛性判别法

2025-09-30 理论教育版权反馈

【摘要】：1.绝对收敛与条件收敛的概念设级数有无穷多个正项，也有无穷多个负项，则称是任意项级数.任意项级数的收敛性分绝对收敛、条件收敛及发散.如果收敛，则称绝对收敛；如果发散，但收敛，则称条件收敛.注（ⅰ）一般地，当发散时，未必发散.但是，如果由正项级数比值判别法或根值判别法判定发散时，则必发散.（ⅱ）如果绝对收敛，则的收敛性与的收敛性相同.如果收敛，发散，则发散.2.交错级数的莱布尼茨定理设an>0（n=1，2，…

【主要内容】

1.绝对收敛与条件收敛的概念

设级数有无穷多个正项，也有无穷多个负项，则称是任意项级数.

任意项级数的收敛性分绝对收敛、条件收敛及发散.

如果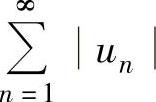收敛，则称绝对收敛；如果发散，但收敛，则称条件收敛.

注（ⅰ）一般地，当发散时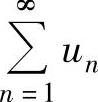，未必发散.但是，如果由正项级数比值判别

法或根值判别法判定发散时，则必发散.

（ⅱ）如果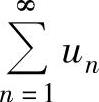绝对收敛，则的收敛性与的收敛性相同.如果收

敛（绝对收敛或条件收敛），发散，则发散.

2.交错级数的莱布尼茨定理

设a_n>0（n=1，2，…），则称级数为交错级数，它是一种特殊的任意项级数.

莱布尼茨定理：设正项数列{a_n}单调减少收敛于零，则交错级数收敛.

注交错级数时，绝对收敛；当0<p≤1时，条件收敛；当p≤0时，发散.

【典型例题】

例4.11.1（单项选择题）设正项级数收敛，则对于常数，级数

A.绝对收敛 B.条件收敛

C.发散 D.收敛性与λ有关

精解由于，所以存在正数M，使得，因此

此外，由收敛知收敛.由此得到收敛，从而绝对收敛.

因此本题选A.

例4.11.2（单项选择题）设，则级数（）.

A.都收敛

B.与都发散

C.收敛而发散

D.发散而收敛

精解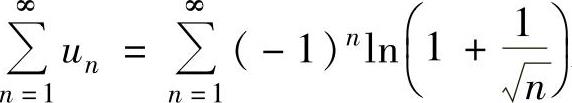是交错级数，记，则{a_n}单调减少(https://www.chuimin.cn)

收敛于零，所以由交错级数的莱布尼茨定理知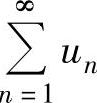收敛.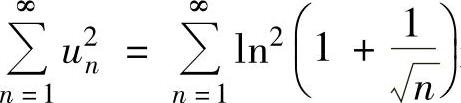是正项级数.由于，

而发散，所以发散.

因此本题选C.

例4.11.3 判别级数的收敛性.如果是收敛的，需指明其是绝对收敛的还是条件收敛的.

精解记，先考虑的收敛性.

由于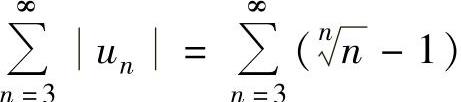，其中且，

所以由发散知发散.

下面考虑的收敛性.

由于是交错级数，且，此外数列u₃，u₄，…

单调减少（这是因为将n看做x，则由得函数，于是由知f（x）在[e，+∞）上单调减少，从而u₃，u₄，…单

调减少），所以由交错级数的莱布尼茨定理知收敛.

综上所述，条件收敛.

例4.11.4 设函数f（x）在[-1，1]上定义，在点x=0处二阶可导，且证明：级数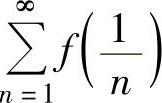绝对收敛.

精解只要证明收敛即可.为此考虑函数f（x）在点x=0的某个邻域内的性态.

由知，f（0）=0，f′（0）=0，此外，，

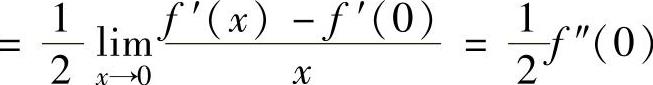所以在点x=0的某个邻域（-δ，δ）（δ是某个正数）内有

f（x）≤Mx²（M是某个正数）.

由此可知存在正整数N，当n>N时，有及

于是，由收敛得证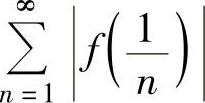收敛，从而绝对收敛.

例4.11.5 判别级数的收敛性.

精解记，将中的看做x得函数

（在点x=0的某个邻域内），

于是，当n充分大时有

由于是p=1的级数，所以条件收敛，此外，

而收敛，所以收敛，即绝对收敛.因此条件收敛.