)上应用拉格朗日中值定理得lnln(n+1)-lnlnn=′x=ξn,即有,并且,即发散,所以由比较判别法知发散.......
2023-10-27
【主要内容】
1.正项级数收敛的充分必要条件
如果un≥0(n=1,2,…),则称 为正项级数.
为正项级数.
正项级数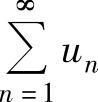 收敛的充分必要条件是它的部分和数列{sn}有上界
收敛的充分必要条件是它的部分和数列{sn}有上界
2.比值判别法
设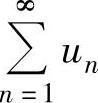 是正项级数.如果
是正项级数.如果 ,则
,则
当ρ<1时, 收敛;
收敛;
当ρ>1时, 发散;
发散;
当ρ=1时,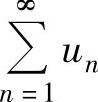 的收敛性要用其他方法判别.
的收敛性要用其他方法判别.
注 当un包含有n!之类的因子,或关于n的若干个因子连乘形式时,往往用比值判别法
判别正项级数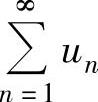 的收敛性.
的收敛性.
3.根值判别法
设 是正项级数,如果
是正项级数,如果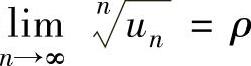 ,则
,则
当ρ<1时,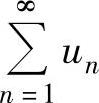 收敛;
收敛;
当ρ>1时,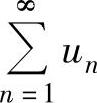 发散;
发散;
当ρ=1时,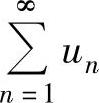 的收敛性要用其他方法判别.
的收敛性要用其他方法判别.
注 当un包含有n或关于n的函数为指数的因子时,往往用根值判别法判别正项级数 的收敛性.
的收敛性.
【典型例题】
例4.9.1 判别正项级数 的收敛性.
的收敛性.
精解 用比值判别法判别.记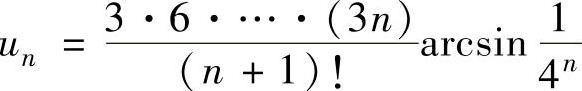 ,则
,则
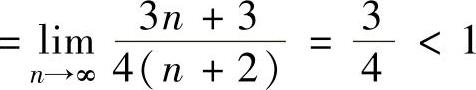 ,
,
所以,所给正项级数收敛.(www.chuimin.cn)
例4.9.2讨论正项级数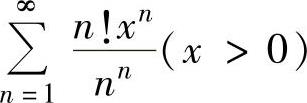 的收敛性与x取值的关系.
的收敛性与x取值的关系.
精解 用比值判别法进行讨论.记 ,则
,则
所以由比值判别法知,当0<x<e时,所给正项级数收敛;当x>e时,所给正项级数发散;
当x=e时,由于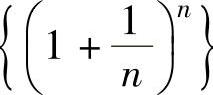 单调增加收敛于e,所以
单调增加收敛于e,所以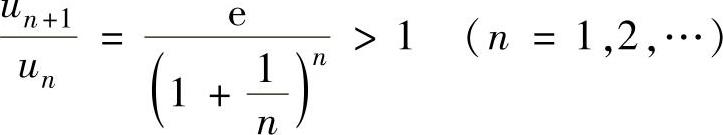 ,
,
即{un}单调增加,于是由un>u1=e(n=2,3,…)知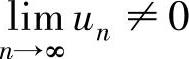 ,由此推出x=e时所给正项
,由此推出x=e时所给正项
级数发散.
例4.9.3 判别正项级数 的收敛性.
的收敛性.
精解 用根值判别法判别收敛性.记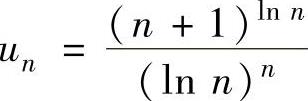 ,则
,则
由于 ,所以
,所以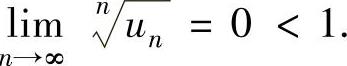 从而所给正项级数收敛.
从而所给正项级数收敛.
例4.9.4 判别正项级数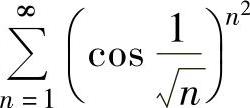 的收敛性.
的收敛性.
精解 用根值判别法判别收敛性.记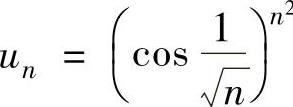 ,则
,则
考虑函数极限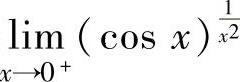 (即将
(即将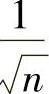 看成x):
看成x): ,(1)
,(1)
其中,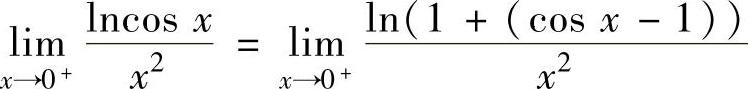
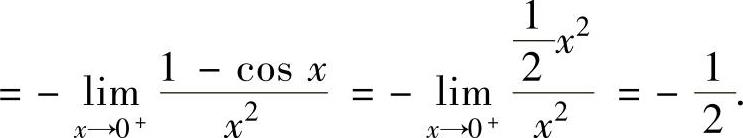
将它代入式(1)得
从而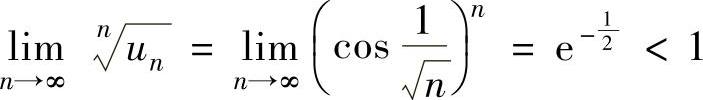 ,因此所给正项级数收敛.
,因此所给正项级数收敛.
例4.9.5 设正项数列{an}单调增加且有上界,证明:级数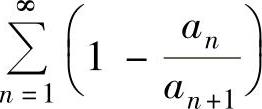 收敛.
收敛.
精解 由{an}单调增加知 ,因此
,因此 是正项级数,
是正项级数,
于是只要证明数列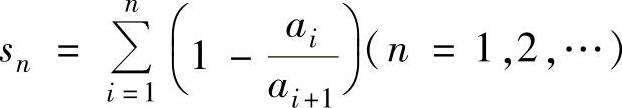 有上界即可.
有上界即可.
记数列{an}的上界为M,则
因此,级数
n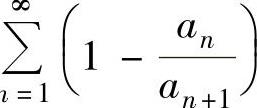 收敛.
收敛.
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

1.绝对收敛与条件收敛的概念设级数有无穷多个正项,也有无穷多个负项,则称是任意项级数.任意项级数的收敛性分绝对收敛、条件收敛及发散.如果收敛,则称绝对收敛;如果发散,但收敛,则称条件收敛.注 (ⅰ)一般地,当发散时,未必发散.但是,如果由正项级数比值判别法或根值判别法判定发散时,则必发散.(ⅱ)如果绝对收敛,则的收敛性与的收敛性相同.如果收敛,发散,则发散.2.交错级数的莱布尼茨定理设an>0(n=1,2,…......
2023-10-27

设{αn}={an+ibn}(n=1,2,···) 为一复数列,表达式称为无穷级数,其前n项的和称为级数的部分和.若该部分和数列收敛,其极限为S,则称上述复数项级数收敛,且称S 为该级数的和,记为若部分和数列{Sn}发散,则称级数发散.定理4 级数 收敛的充要条件是其实部级数和虚部级数都收敛.证明 因其中σn =a1+a2+···+an,τn =b1+b2+···+bn 分别为 的部分和.由定理2......
2023-10-30

设α1,α2,··· ,αn,··· 为一个复数列,其通项为α=an+ibn,可简记该复数列为{αn}.定义1 设{αn}为一个复数列且α = a+ib为复常数.若对任意正数ε都存在对应的正整数N,使当n >N时恒有|αn-α| <ε,则称该复数列收敛且其极限为α,记为这时也称复数列{αn}收敛于α,如果不存在任何有限复常数α使得复数列{αn} 收敛于α,则称复数列{αn}是发散的.由复数列{αn......
2023-10-30

特征的判别性则要求样本的特征分布为类内紧凑和类间可分。类内距离的loss项即centerloss[4],公式如式所示:式中,cyi∈Rd表示第yi类深度学习特征的中心。类间距离的loss项公式如式所示:目标是最小化类内距离与最大化类间距离,将LC与LW结合得到判别特征loss,如式所示:对于每次迭代,需要计算LD关于xi的梯度用于计算卷积网络的反向梯度用于更新权值,同样需要更新cyi,分别如式、式所示。......
2023-10-21

以下我们来讨论两个总体的距离判别,分别讨论两个总体协方差矩阵相同和不同的情况.设总体X1 和X2 的均值向量分别为μ1 和μ2,协方差矩阵分别为Σ1 和Σ2.给定一个样本x,要判断x 来自哪个总体.首先考虑两个总体X1 和X2 的协方差矩阵相同的情况,即μ1 ≠μ2,Σ1=Σ2=Σ.要判断x 来自哪个总体,需要计算x 到总体X1 和X2 的马氏距离的平方d2(x,X1)和d2(x,X2),然后进行......
2023-11-18

对于一元二次方程ax2+bx+c=0(a≠0).当b2-4ac>0时,方程_______________________;当b2-4ac=0时,方程________________________;当b2-4ac<0时,方程_______________________.1.方程4x2-3x+1=0的根的情况是( ).A.有两个都是负的实数根B.有两个都是正的实数根C.有两个相等的实数根D.没有实......
2023-07-03
相关推荐