首页 理论教育级数的收敛性与性质：全面复习与常考知识点解析

级数的收敛性与性质：全面复习与常考知识点解析

2025-09-30 理论教育 版权反馈
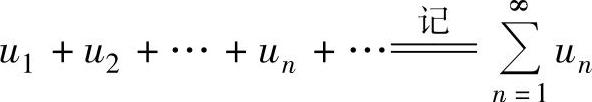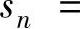
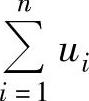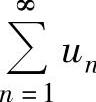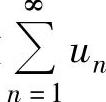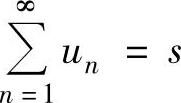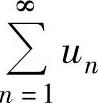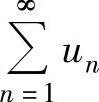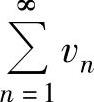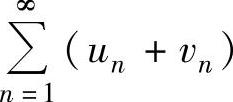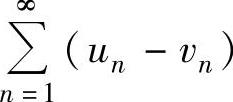【摘要】：【主要内容】1.级数收敛性的概念设数列{un}，则称记号为无穷级数，简称级数.记，则称{sn}为级数的部分和数列.如果{sn}收敛于s，则称级数收敛，且称s为该级数的和，记为；如果{sn}发散，则称级数发散.2.收敛级数的基本性质（1）如果级数和分别收敛于u与v，则级数和都收敛，它们的和分别为u+v和u-v.（2）如果级数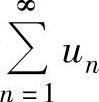收敛，k为常数，则级数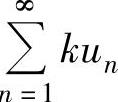收敛，且当时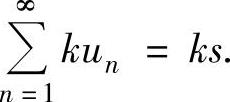，（3）如果级数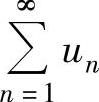收敛，则在它的前面任意添加

【主要内容】

1.级数收敛性的概念

设数列{un}，则称记号978-7-111-46245-3-Part01-2152.jpg为无穷级数，简称级数.记978-7-111-46245-3-Part01-2153.jpg978-7-111-46245-3-Part01-2154.jpg，则称{sn}为级数978-7-111-46245-3-Part01-2155.jpg的部分和数列.如果{sn}收敛于s，则称级数978-7-111-46245-3-Part01-2156.jpg收敛，且称s

为该级数的和，记为978-7-111-46245-3-Part01-2157.jpg；如果{sn}发散，则称级数978-7-111-46245-3-Part01-2158.jpg发散.

2.收敛级数的基本性质

（1）如果级数978-7-111-46245-3-Part01-2159.jpg和978-7-111-46245-3-Part01-2160.jpg分别收敛于u与v，则级数978-7-111-46245-3-Part01-2161.jpg和978-7-111-46245-3-Part01-2162.jpg都收

敛，它们的和分别为u+v和u-v.

（2）如果级数978-7-111-46245-3-Part01-2163.jpg收敛，k为常数，则级数978-7-111-46245-3-Part01-2164.jpg收敛，且当978-7-111-46245-3-Part01-2165.jpg时，978-7-111-46245-3-Part01-2166.jpg

（3）如果级数978-7-111-46245-3-Part01-2167.jpg收敛，则在它的前面任意添加有限项、去掉或改变它开头的有限项而成的级数仍收敛.

（4）如果级数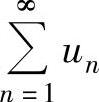978-7-111-46245-3-Part01-2168.jpg收敛，则对它的项任意加括号后所得级数仍收敛，且其和不变.

（5）如果级数收敛，则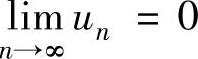978-7-111-46245-3-Part01-2169.jpg（级数收敛的必要条件）.

3.常用级数收敛性

（1）级数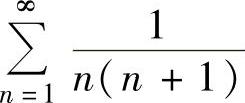978-7-111-46245-3-Part01-2170.jpg收敛，且其和为1.

（2）等比级数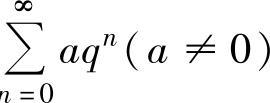978-7-111-46245-3-Part01-2171.jpg：当0<q<1时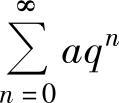，978-7-111-46245-3-Part01-2172.jpg收敛，且其和为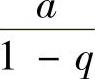978-7-111-46245-3-Part01-2173.jpg；当q≥

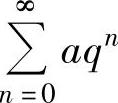1时，978-7-111-46245-3-Part01-2174.jpg发散.

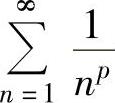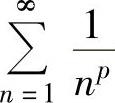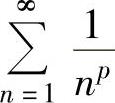（3）p级数978-7-111-46245-3-Part01-2175.jpg：当p>1时，978-7-111-46245-3-Part01-2176.jpg收敛；当p≤1时，978-7-111-46245-3-Part01-2177.jpg发散.

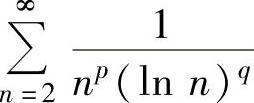（4）978-7-111-46245-3-Part01-2178.jpg：当p>1或p=1而q>1时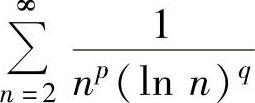，978-7-111-46245-3-Part01-2179.jpg收敛；当p<1或p=1

而q≤1时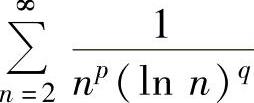，978-7-111-46245-3-Part01-2180.jpg发散.

【典型例题】

例4.8.1（单项选择题） 设有命题

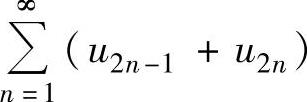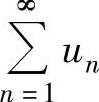① 如果978-7-111-46245-3-Part01-2181.jpg收敛，则978-7-111-46245-3-Part01-2182.jpg收敛.

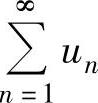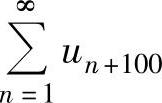② 如果978-7-111-46245-3-Part01-2183.jpg收敛，则978-7-111-46245-3-Part01-2184.jpg收敛.

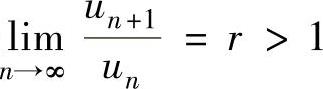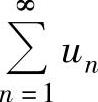③ 如果978-7-111-46245-3-Part01-2185.jpg，则978-7-111-46245-3-Part01-2186.jpg发散.

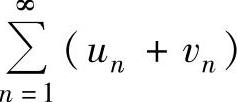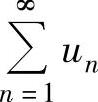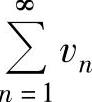④ 如果978-7-111-46245-3-Part01-2187.jpg收敛，则978-7-111-46245-3-Part01-2188.jpg和978-7-111-46245-3-Part01-2189.jpg都收敛.则以上命题中正确的是（ ）.

A.①② B.②③ C.③④ D.①④(https://www.chuimin.cn)

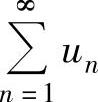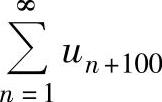精解 由收敛级数基本性质知，当978-7-111-46245-3-Part01-2190.jpg收敛时，978-7-111-46245-3-Part01-2191.jpg收敛，所以命题②正确.

所以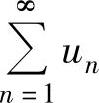978-7-111-46245-3-Part01-2198.jpg发散.所以命题③正确.

因此本题选B.

例4.8.2（单项选择题） 设由收敛级数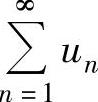978-7-111-46245-3-Part01-2199.jpg构造以下级数

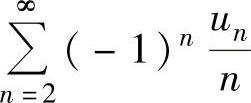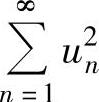①978-7-111-46245-3-Part01-2200.jpg，②978-7-111-46245-3-Part01-2201.jpg，

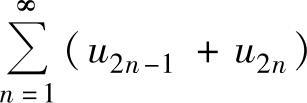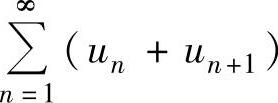③978-7-111-46245-3-Part01-2202.jpg，④978-7-111-46245-3-Part01-2203.jpg，

则上面四个级数中必收敛的是（ ）.

A.①② B.②③ C.③④ D.①④

精解 由于③是对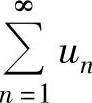978-7-111-46245-3-Part01-2204.jpg两项加括号而成的级数，所以由收敛级数的基本性质知，③必收敛.

由于④是两个收敛级数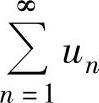978-7-111-46245-3-Part01-2205.jpg与978-7-111-46245-3-Part01-2206.jpg相加而成的级数，所以由收敛级数的基本性质

知，④必收敛.

因此本题选C.

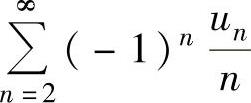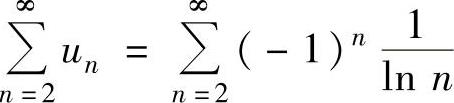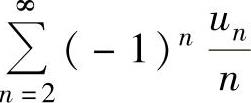
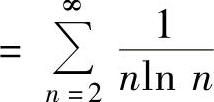注 （ⅰ）978-7-111-46245-3-Part01-2207.jpg未必收敛.例如978-7-111-46245-3-Part01-2208.jpg收敛，但978-7-111-46245-3-Part01-2209.jpg978-7-111-46245-3-Part01-2210.jpg发散.

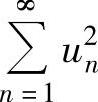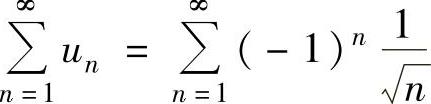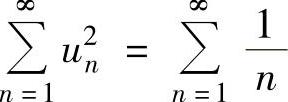（ⅱ）978-7-111-46245-3-Part01-2211.jpg也未必收敛，例如978-7-111-46245-3-Part01-2212.jpg收敛，但978-7-111-46245-3-Part01-2213.jpg发散.

例4.8.3（单项选择题） 如果级数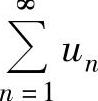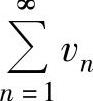978-7-111-46245-3-Part01-2214.jpg，978-7-111-46245-3-Part01-2215.jpg都发散，则（ ）.

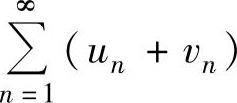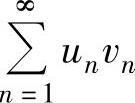A.978-7-111-46245-3-Part01-2216.jpg必发散B.978-7-111-46245-3-Part01-2217.jpg必发散

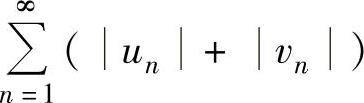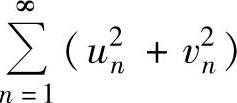C.978-7-111-46245-3-Part01-2218.jpg必发散D.978-7-111-46245-3-Part01-2219.jpg必发散

精解 选项A，B，D是不正确的.例如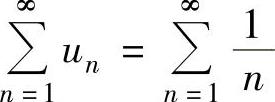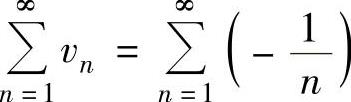978-7-111-46245-3-Part01-2220.jpg，978-7-111-46245-3-Part01-2221.jpg都是发散级数，

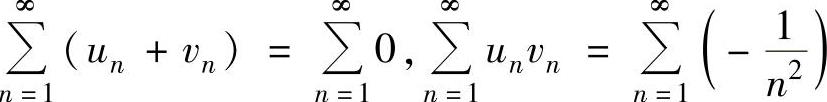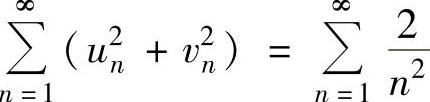但978-7-111-46245-3-Part01-2222.jpg，978-7-111-46245-3-Part01-2223.jpg都是收敛的.

因此本题选C.

例4.8.4 求级数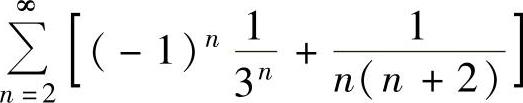978-7-111-46245-3-Part01-2224.jpg的和.

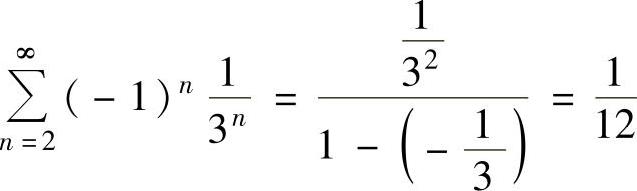精解978-7-111-46245-3-Part01-2225.jpg，

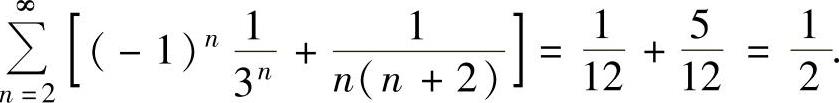
所以，978-7-111-46245-3-Part01-2227.jpg

相关文章

  • 罗尔定理和应用-基础篇全面复习与常考知识点解 罗尔定理和应用-基础篇全面复习与常考知识点解

    【主要内容】1.罗尔定理设函数f（x）在[a，b]上连续，在（a，b）内可导，且f（a）=f（b），则存在ξ∈（a，b），使得f′（ξ）=0.罗尔定理有各种推广形式，例如（1）设函数f（x）在（a，b）内可导，且与存在且相等，则存在ξ∈（a，b），使得f′（ξ）=0.（2）设函数f（x）在[a，+∞）上连续，在（a，+∞）上可导，且，则存在ξ∈（a，+∞），使得f′（ξ）=0.2.罗尔定理应用方法......

    2025-09-30

    详细阅读
  • 方程实根个数判定-基础篇全面复习与常考知识点 方程实根个数判定-基础篇全面复习与常考知识点

    【主要内容】1.设函数f（x）在[a，b]上连续，且f（a）f（b）<0，则方程f（x）=0在（a，b）内有实根.这一结论有各种推广形式，例如，（1）设函数f（x）在（a，b）内连续，且，则方程f（x）=0在（a，b）内有实根.（2）设函数f（x）在[a，+∞）上连续，且，则方程f（x）=0在[a，+∞）上有实根.2.设f（x）是[a，b]上的连续单调函数，且f（a）f（b）<0，则方程f（x）=......

    2025-09-30

    详细阅读
  • 不等式导数的证明-基础篇全面复习与常考知识点 不等式导数的证明-基础篇全面复习与常考知识点

    【主要内容】函数不等式f（x）0（x∈（a，b））及时，有F（......

    2025-09-30

    详细阅读
  • 定积分不等式证明-基础篇全面复习与常考知识点 定积分不等式证明-基础篇全面复习与常考知识点

    【主要内容】含定积分的不等式的常见证明方法是导数方法，即将欲证不等式中所包含的定积分上限字母换成x（如果包含的定积分多于一个，则选择其中一个，将其上限字母换成x），同时将该不等式中与此相同的字母都换成x，得到一个函数不等式，然后用导数方法证明这个函数不等式成立，由此即证得欲证的不等式.【典型例题】例2.9.1 设函数f（x）在[0，+∞）上连续且单调增加.证明：满足0

    2025-09-30

    详细阅读
  • 函数可导与导数的概念：数学考研常考知识点解析 函数可导与导数的概念：数学考研常考知识点解析

    【主要内容】1.函数在点x0处可导与导数的定义设函数f（x）在点x0的某个邻域内有定义.如果极限存在，则称f（x）在点x0处可导，且称这个极限的值为f（x）在点x0处的导数，记为f′（x0）或注 函数在点x0处可导，必在点x0处连续，但反之未必正确.函数f（x）在点x0处可导的充分必要条件是f（x）在点x0处的左导数f-′（x0）和右导数都存在且相等.注 当x0是分段函数的分段点时，要判定f（x）......

    2025-09-30

    详细阅读
  • 二重积分计算及常考知识点解析 二重积分计算及常考知识点解析

    ，Δσn，其中Δσi表示第i个小闭区域，也表示它的面积，在每个小闭区域Δσi上任取一点（i=1，2，…......

    2025-09-30

    详细阅读
  • 函数连续定义和常考知识点 函数连续定义和常考知识点

    ，精解 按定义只要检验是否成立即可.由，知，所以f在点x=1处连续.例1.4.2 设函数在点x=0处连续，求常数a，b.精解 根据f在点x=0处连续的充分必要条件有，其中，，，f=b.将它们代入式得4a=2=b，即，b=2.例1.4.3 设函数，那么如何定义f的值，使得f在点x=0处连续.精解 由函数在点x=0处连续的定义知，只要即可.由于，其中，将它代入式得因此，定义，使得f在点x=0处连续.......

    2025-09-30

    详细阅读
  • 曲线凹凸性、拐点计算：全面复习与解析 曲线凹凸性、拐点计算：全面复习与解析

    1.曲线凹凸性及其判定方法在某个区间内，如果曲线位于其上任意一点的切线的上方（下方），则称曲线在该区间内为凹的（凸的）.曲线y=f（x）在区间I上凹凸性的判定方法是：设函数f（x）在I上二阶可导.如果f″（x）>0（x∈I），则曲线y=f（x）在I上是凹的；如果f″（x）<0（x∈I），则曲线y=f（x）在I上是凸的.2.曲线拐点及其计算方法设函数f（x）连续，则曲线y=f（x）上的凹弧与凸弧的分......

    2025-09-30

    详细阅读