知识要点1.微分方程的基本概念:微分方程的定义、阶、通解、特解.2.可分离变量的微分方程:求解可分离变量微分方程的步骤:(1)分离变量;(2)两端分别积分,可得原方程的通解.如果问题为求特解,只需将初始条件代入求得的通解,确定常数C的值即可.3.一阶线性非齐次微分方程:形式:y′+P(x)y=Q(x).求解方法有以下两种:(1)常数变易法:第一步,先求对应的齐次微分方程y′+P(x)y=0的通解......
2025-09-30
【主要内容】
设a是非零常数,f(t)是已知函数,则称yt+1+ayt=f(t)(t=0,1,2,…)(∗)
(这里yt=φ(t)是未知函数)为一阶常系数线性差分方程.当自由项f(t)≡0时,式(∗)成为yt+1+ayt=0(t=0,1,2,…).
上式就是式(∗)对应的一阶常系数齐次线性差分方程.(∗∗)
如果函数yt=φ(t)代入式(∗)或(式(∗∗)),使之对t=0,1,2,…成为恒等式,则称yt=φ(t)是式(∗)或(∗∗)的解.式(∗)(或(∗∗))的包含有一个任意常数的解,称为式(∗)(或(∗∗))的通解;当通解中的任意常数被初始条件y0=A确定时的解,称为特解.
式(∗)的通解为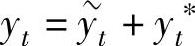 ,其中
,其中 是式(∗∗)的通解,yt∗是式(∗)的特解.
是式(∗∗)的通解,yt∗是式(∗)的特解.
1.一阶常系数齐次线性差分方程的通解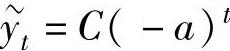 (其中C是任意常数).
(其中C是任意常数).
2.一阶常系数非齐次线性差分方程的特解
(1)当f(t)=dt·Pn(t)(其中Pn(t)是已知的n次多项式,d是非零常数)时,式(∗)有特解
yt∗=tk·dtQn(t).其中,k=0,a+d≠0,
{1,a+d=0,Qn(t)是待定的n次多项式,它的系数可通过将yt∗代入式(∗)确定.
(2)当f(t)=b1cosωt+b2sinωt(其中ω≠0,且b1,b2是不同时为零的常数)时,式(∗)有特解
yt∗=tk(αcosωt+βsinωt),
其中,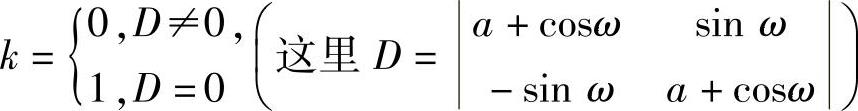 ,α,β为待定常数,可将yt∗代入式(∗)确
,α,β为待定常数,可将yt∗代入式(∗)确
定.
注设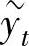 和
和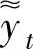 分别是一阶常系数非齐次线性差分方程yt+1+ayt=f1(t)和yt+1+ayt=
分别是一阶常系数非齐次线性差分方程yt+1+ayt=f1(t)和yt+1+ayt=
f2(t)的特解,则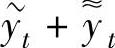 是yt+1+ayt=f1(t)+f2(t)的特解.(https://www.chuimin.cn)
是yt+1+ayt=f1(t)+f2(t)的特解.(https://www.chuimin.cn)
【典型例题】
例4.7.1 求差分方程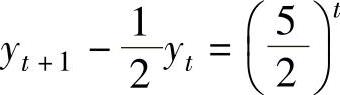 的通解.
的通解.
精解 所给差分方程是一阶常系数非齐次线性差分方程,它对应的齐次线性差分方程为
其通解为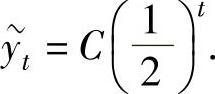 而所给的差分方程应有形如
而所给的差分方程应有形如
的特解.将它代入所给的差分方程得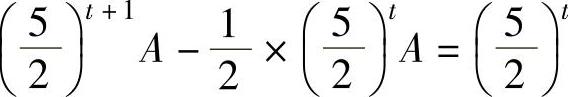 ,即
,即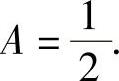
将它代入式(1)得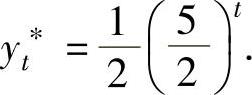 于是所给的差分方程的通解为
于是所给的差分方程的通解为
例4.7.2 求差分方程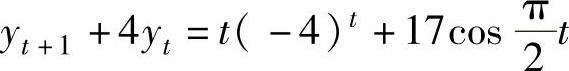 满足y0=1的特解.
满足y0=1的特解.
精解 所给差分方程是一阶常系数非齐次线性差分方程,它对应的齐次线性差分方程为
yt+1+4yt=0,
其通解为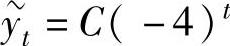 ,而所给的差分方程应有形如
,而所给的差分方程应有形如
(1)的特解,将它代入所给的差分方程得
比较上式两边t的同次幂的系数及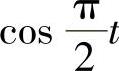 ,
,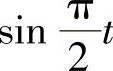 的系数得
的系数得
解此方程组得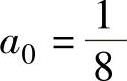 ,
,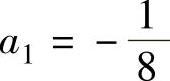 ,α=4,β=1.将它代入式(1)得
,α=4,β=1.将它代入式(1)得
因此,所给差分方程的通解为
在式(2)中令t=0,并将y0=1代入得1=C+4,即C=-3.
于是所求的特解为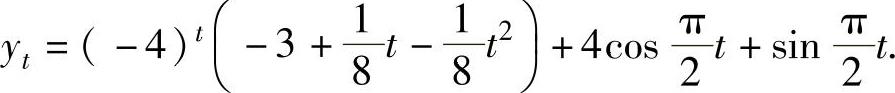
相关文章

知识要点1.微分方程的基本概念:微分方程的定义、阶、通解、特解.2.可分离变量的微分方程:求解可分离变量微分方程的步骤:(1)分离变量;(2)两端分别积分,可得原方程的通解.如果问题为求特解,只需将初始条件代入求得的通解,确定常数C的值即可.3.一阶线性非齐次微分方程:形式:y′+P(x)y=Q(x).求解方法有以下两种:(1)常数变易法:第一步,先求对应的齐次微分方程y′+P(x)y=0的通解......
2025-09-30

离散系统的动态过程用建立在差分、差商等概念基础上的差分方程来描述。k阶线形差分方程的一般形式为式中,r——输入量;c——输出量。各阶差分的变换函数例8-7 用Z变换法求二阶差分方程:y(k+2)+3y(k+1)+2y=r。解:利用超前定理,对差分方程进行Z变换,得z2Y-z2y-zy+3[zY-zy]+2Y=R将已知条件代入上式,得所以,利用部分分式法求Y的Z反变换所以,作Z 反变换,......
2025-09-29

【主要内容】1.设函数f(x)在[a,b]上连续,且f(a)f(b)<0,则方程f(x)=0在(a,b)内有实根.这一结论有各种推广形式,例如,(1)设函数f(x)在(a,b)内连续,且,则方程f(x)=0在(a,b)内有实根.(2)设函数f(x)在[a,+∞)上连续,且,则方程f(x)=0在[a,+∞)上有实根.2.设f(x)是[a,b]上的连续单调函数,且f(a)f(b)<0,则方程f(x)=......
2025-09-30

所以为了节省内存,平差示例程序中采用一维数组保存法方程系数,并且只保存主对角线以上的数值,因而法方程系数阵称为上三角阵。例如pibidi中bi、di在误差方程系数数组中的下标分别是2、4,填充到法方程系数阵二维数组变量中的下标就是(2,4)。......
2025-09-30

差分脉冲编码调制的系统原理如图 5-6-1 所示。图5-6-1差分脉冲编码调制的系统原理图图 5-6-1 中,发送端编码器中的预测器与接收端解码器中的预测器是完全一样的,因此,在信道传输无误码的情况下,接收端解码器输出的重构信号Sr与编码器的Sr信号是完全相同的。例如,在较好图像质量的情况下,每一抽样值只需 4 bit 缩码即可,因此大大压缩了传送的比特率。......
2025-09-29

据图4-6的极坐标利用变换:并利用r 0和Φ0表示式(4-6),可得以及利用标准数理推导,可以推导出卫星轨道半径r 0的方程为式中,θ0为常数,e为椭圆的偏心率,椭圆的半焦弦p为式中,h为卫星环绕角动量的大小。轨道方程是椭圆方程,即开普勒行星运动第一定律。根据式可以计算出GEO卫星的轨道半径,此时,周期T等于地球的自转周期,这样才能保证卫星在赤道上的某点与地球保持相对静止状态。......
2025-09-29

根据叠加原理,式可写成以下形式:图14-12位移条件式就是为求解多余未知力X1和X2所需要建立的力法方程。对于高次超静定问题,其力法方程也可类似推出。当原结构在去掉多余约束处的已知位移为零时,其力法方程为方程中的系数称为柔度系数,位于主对角线上的系数δii称为主系数,在主对角线两侧的系数δij称为副系数,Δ1P称为自由项。由于基本体系是静定的,所以力法方程中各系数和自由项都可以按照上一单元位移计算的方法求出。......
2025-09-29

高斯约化的基本原理实际上是通过加减消元的方法,对法方程系数阵和常数阵进行线性变换,将法方程系数阵变成上三角阵。以加减消元法对线性方程系数和常数组成的行进行消元变换,实际上是将其各元素减去另一行同列元素乘一个不为0的数,从而将某一未知数的系数变为0。由于法方程系数阵具有对称性这一特征,所以高斯约化法虽然原理与加减消元法相同,但是有其独特的规律。......
2025-09-30
相关推荐