首页理论教育解方程y（x）=∫0xg（x，y（t））dt+h（x）的方法

解方程y（x）=∫0xg（x，y（t））dt+h（x）的方法

2025-09-30 理论教育版权反馈

【摘要】：【主要内容】求满足方程y（其中，g（x，u）是已知的连续函数，h（x）是已知的可微函数）的连续函数y（t）的步骤如下：（1）将g（x，y（t））中的x移走，例如移出到积分号外，或通过适当的变量代换移到积分上限.（2）经过上述处理后的方程两边对x求导（一次或两次）转换成微分方程，求解此微分方程（此时的初始条件可从所给的方程中得到），即得未知函数y（x）的表达式.【典型例题】例4.6.1 求满足方程的

【主要内容】

求满足方程y（其中，g（x，u）是已知的连续函数，h（x）是已知的可微函数）的连续函数y（t）的步骤如下：

（1）将g（x，y（t））中的x移走，例如移出到积分号外，或通过适当的变量代换移到积分上限.

（2）经过上述处理后的方程两边对x求导（一次或两次）转换成微分方程，求解此微分方程（此时的初始条件可从所给的方程中得到），即得未知函数y（x）的表达式.

【典型例题】

例4.6.1 求满足方程的连续函数y（x）（x≥1）.

精解由y（x）连续知∫可导，从而由所给方程知y（x）（x≥1）可导.因此，所给方程两边对x求导得

y²（x）=2xy（x）+x²y′（x），

即

令y=xu，代入式（1）得，即

上式两边分别积分得，即由此得到

由所给的方程知y（1）=1.将它代入式（2）得，即C=-2.将它代入式（2）得

例4.6.2 设φ（x）是连续函数，且满足方程

求φ（x）.

精解将所给方程改写成

（即将被积函数中的x移出积分号），并在上式两边对x求导（由于φ（x）连续，所以由上列表达式知φ（x）可导）得

即

式（1）两边对x求导得

φ″（x）=e^x-φ（x），即φ″（x）+φ（x）=e^x.（2）

它有特解.此外它对应齐次线性微分方程φ″（x）+φ（x）=0的通解为

Φ=C₁sinx+C₂cosx.因此式（2）的通解为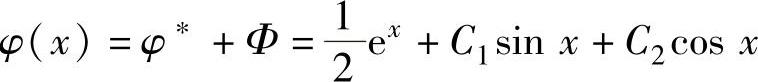，（3）

并且

由题设中所给的方程及式（1）知φ（0）=1，φ′（0）=1.将它们代入式（3）和式（4）得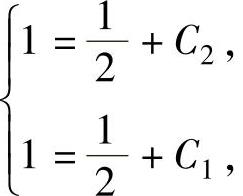即

将它们代入式（3）得(https://www.chuimin.cn)

例4.6.3 设函数y（x）具有连续导数，且满足方程

及y（0）=1，求y（x）的表达式.

精解首先应由变量代换u=xt将中的x移到积分上限：

将它代入所给方程得

上式两边对x求导得y″+3y′+2y=e^-x（二阶常系数非齐次线性微分方程）（1）

式（1）对应的齐次线性微分方程为y″+3y′+2y=0，（2）

它的特征方程r²+3r+2=0有根r=-1，-2，所以式（2）的通解为Y=C₁e^-x+C_2e^-2x.此外，式（1）有特解y∗=Axe^-x.将它代入式（1）得（Axe^-x）″+3（Axe^-x）′+2（Axe^-x）=e^-x，

即A（x-2）e^-x+3A（1-x）e^-x+2Axe^-x=e^-x.

化简得A=1，所以式（1）有特解y∗=xe^-x.从而式（1）的通解为y（x）=C₁e^-x+C₂e^-2x+xe^-x，（3）

且y′（x）=-C₁e^-x-2C₂e^-2x+（1-x）e^-x.（4）由题设知y（0）=1，此外由所给方程知y′（0）=-1，将它们代入式（3）、式（4）得即C₁=0，C₂=1.将它们代入式（3）得所求的

y（x）=e^-2x+xe^-x.

例4.6.4 设连续函数y（x）满足方程，

且存在，求y（x）的表达式.

精解将前的x除去得

上式两边分别对x求导得，

化简后得（可降阶的二阶微分方程）（1）

令p=y′，则式（1）成为（一阶线性微分方程）.

它的通解为

于是式（1）的通解为

下面确定式（2）中的C₁与C2.

由存在知C₁=0，所以

将x=1代入所给的方程得y（1）=1+y′（1）.于是由式（3）得，即

将它代入式（3）得