一、二阶常系数非齐次线性方程解的结构定理5若y*是二阶常系数线性非齐次方程的一个特解，Y=c1y1+c2y2是方程（1）对应的二阶常系数线性齐次方程的通解，则是方程（1）的通解.二、二阶常系数非齐次线性方程的解法下面我们根据f（x）具有下列特殊情形时，来给出求其特解的公式：【例题1】求方程y″+4y′+3y=x-2的一个特解.解：对应的特征方程为p2+4p+3=0.原方程右端不出现eμx，但可......
2023-11-20
二阶常系数非齐次线性微分方程解析
【摘要】：【主要内容】形如y″+py′+qy=f（x）（）（其中p，q是常数，f（x）是已知函数，且不恒为零）的微分方程，称为二阶常系数非齐次线性微分方程，称y″+py′+qy=0（）是式（）对应的齐次线性微分方程.如果Y（x）是式（）的通解，y（x）是式（）的一个特解，则y（x）=Y（x）+y（x）是式（）的通解.关于二阶常系数非齐次线性微分方程（）的特解有以下结论：（1）当f（x）=Pm（x）eλx（其
【主要内容】
形如
y″+py′+qy=f（x）（∗）（其中p，q是常数，f（x）是已知函数，且不恒为零）的微分方程，称为二阶常系数非齐次线性微分方程，称
y″+py′+qy=0（∗∗）是式（∗）对应的齐次线性微分方程.
如果Y（x）是式（∗∗）的通解，y∗（x）是式（∗）的一个特解，则
y（x）=Y（x）+y∗（x）是式（∗）的通解.
关于二阶常系数非齐次线性微分方程（∗）的特解有以下结论：
（1）当f（x）=Pm（x）eλx（其中λ是常数，Pm（x）是关于x的m次已知多项式）时，式（∗）有特解
y∗=xkQm（x）eλx，其中，k按λ是方程y″+py′+qy=0的特征方程的零重根（即不是特征方程的根）、一重根、二重根对应地取0，1，2，Qm（x）是x的m次多项式，其系数可将y∗=xkQm（x）eλx代入式（∗）确定.
（2）当f（x）=eαx[Pl（x）cosβx+Pn（x）sinβx]（其中α，β都是常数，Pl（x），Pn（x）分别是关于x的l次和n次已知多项式）时，式（∗）有特解
y∗=xk[Rm（1）（x）cosβx+Rm（2）（x）sinβx]eαx，其中，k按α+iβ是方程y″+py′+qy=0的特征方程的零重根、一重根对应地取0，1，Rm（1）（x），Rm（2）（x）都是关于x的m（m=max{l，n}）次多项式，它们的系数可将y∗=xk[Rm（1）（x）cosβx+Rm（2）（x）sinβx]eαx代入式（∗）确定.
【典型例题】
例4.5.1 （单项选择题）函数y=C1ex+C2e-2x+xex满足的一个微分方程为（）.
A.y″-y′-2y=3xex B.y″-y′-2y=3ex
C.y″+y′-2y=3xexD.y″+y′-2y=3ex
精解 y应是常系数齐次线性微分方程
y″+p1y′+p2y=f（x）（1）的通解，其中C1ex+C2e-2x是y″+p1y′+p2y=0的通解，所以它的特征方程有根r=1，-2，于是p1=-（1-2）=1，p2=1×（-2）=-2.将它们代入式（1）得
y″+y′-2y=f（x）.（2）
由于xex是式（2）的特解，所以
f（x）=（xex）″+（xex）′-2（xex）=（x+2）ex+（x+1）ex-2xex=3ex.
因此本题选D.
例4.5.2 设二阶常系数齐次线性微分方程y″+ay′+by=0的通解为y=（C1+C2x）ex，求二阶常系数非齐次线性微分方程y″+ay′+by=x满足初始条件y（0）=2，y′（0）=0的特解.
精解 由于
y″+ay′+by=0（1）的通解为（C1+C2x）ex，所以式（1）的特征方程r2+ar+b=0有根r=1（二重），从而a=-（1+1）=-2，b=1×1=1.因此y″+ay′+by=x为
y″-2y′+y=x.（2）
式（2）有特解A+Bx，将它代入式（2）得
-2B+A+Bx=x.
于是有
即A=2，B=1，所以方程（2）有特解2+x.从而式（2）的通解为
y=（C1+C2x）ex+2+x，（3）
并且y′=（C1+C2+C2x）ex+1.（4）
将y（0）=2，y′（0）=0代入式（3）、式（4）得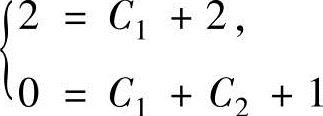
{即C1=0，C2=-1.，
将它们代入式（3）得所求微分方程的特解为
y=-xex+2+x=x（1-ex）+2.
例4.5.3 已知y1=xex+e2x，y2=xex+e-x，y3=xex+e2x-e-x是某非齐次线性微分方程的三个解，求此微分方程.(www.chuimin.cn)
精解 设所求的非齐次线性微分方程为
y″+p1y′+p2y=f（x）（其中p1，p2为常数），（1）则y1-y3=e-x，（y1-y2）+（y1-y3）=e2x都是式（1）对应的齐次线性微分方程
y″+p1y′+p2y=0（2）的解，从而式（2）的特征方程
r2+p1r+p2=0有根r=-1，2，所以p1=-（-1+2）=-1，p2=（-1）×2=-2.将它们代入式（1）得
y″-y′-2y=f（x）.（3）
由于y1是式（3）的解，其中e2x是对应的齐次线性微分方程的特解，所以xex是式（3）的特解，从而
f（x）=（xex）″-（xex）′-2xex
=（x+2）ex-（x+1）ex-2xex=（1-2x）ex.将它代入式（3）得所求的微分方程为
y″-y′-2y=（1-2x）ex.
例4.5.4 求微分方程y″+2y′-3y=e-3x的通解.
精解 所给的微分方程
y″+2y′-3y=e-3x（1）是二阶常系数非齐次线性微分方程，它对应的齐次线性微分方程
y″+2y′-3y=0（2）的特征方程r2+2r-3=0的根为r=-3，1，所以式（2）的通解为
Y=C1e-3x+C2ex.
此外，式（1）有特解
y∗=Axe-3x.（3）将它代入式（1）得
（Axe-3x）″+2（Axe-3x）′-3（Axe-3x）=e-3x，
即 A（-6+9x）e-3x+2A（1-3x）e-3x-3Axe-3x=e-3x.
化简后得-4A=1，即
将它代入式（3）得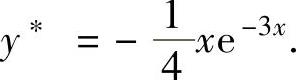
因此，式（1）的通解为
例4.5.5 求微分方程y″+y=x+cosx的通解.
精解 所给的微分方程
y″+y=x+cosx（1）是二阶常系数非齐次线性微分方程，它对应的齐次线性微分方程为
y″+y=0，（2）其特征方程r2+1=0的特征根为i，-i，所以式（2）的通解为
Y=C1cosx+C2sinx.
此外，式（1）有特解
y∗=a0+a1x+x（bcosx+csinx）.（3）（注意：由于y″+y=x应有特解a0+a1x，y″+y=cosx应有特解x（bcosx+csinx），所以y″+y=x+cosx有特解a0+a1x+x（bcosx+csinx））.
将式（3）代入式（1）得
[a0+a1x+x（bcosx+csinx）]″+[a0+a1x+x（bcosx+csinx）]=x+cosx，即[2ccosx-2bsinx+x（-bcosx-csinx）]+[a0+a1x+x（bcosx+csinx）]=x+cosx，化简后成为
a0+a1x+2ccosx-2bsinx=x+cosx，
由此得到
将它们代入式（3）得
因此，式（1）的通解为
有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章
- 详细阅读
-
二阶常系数齐次线性微分方程-2015考研数学详细阅读
【主要内容】形如y″+py′+qy=0 （其中，p，q是常数）（）的微分方程，称为二阶常系数齐次线性微分方程.如果y1（x），y2（x）是式（）的两个线性无关的特解，则y=C1y1（x）+C2y2（x）是式（）的通解.称r2+pr+q=0为式（）的特征方程.关于式（）的通解有以下结论：（1）如果特征方程有两个不等的实根r1，r2，则式（）的通解为（2）如果特征方程有两个相等的实根r1，r2（r1=......
2023-10-27
-
高等数学基础：二阶常系数齐次线性微分方程详细阅读
回答是否定的，因为根据通解的定义，只有当c1，c2这两个常数相互独立时才是的通解.y1，y2在满足什么样的条件下，才能使得c1，c2相互独立呢？......
2023-11-20
- 详细阅读
-
解常系数线性常微分方程：的方法详细阅读
1.用拉氏变换解初值问题的步骤如下：1° 设方程的未知函数y =y(t)的拉氏变换为L[y(t)] = Y (p);2° 对方程进行拉氏变换,利用拉氏变换的线性性质,微分性质（连带着初始条件）等,得到一个关于象函数Y (p) 的代数方程;3° 解象函数的代数方程,解得Y (p);4° 对Y (p),求其逆变换,得到Y (p) 的象原函数y(t) 就是该初值问题的解.这一解法的示意图如下：用拉氏变换......
2023-10-30
-
《高等数学》中一、二阶齐次线性微分方程解的结详细阅读
二阶齐次线性方程的解具有下列性质：定理1 如果函数y1与y2是方程的两个解，那么也是方程的解，其中C1、C2是任意常数.齐次线性方程的这个性质表明它的解符合叠加原理.函数的线性相关与线性无关：定义1 设y1，y2，…......
2023-10-19
-
一阶常系数线性差分方程解析详细阅读
设a是非零常数，f是已知函数，则称yt+1+ayt=f（t=0，1，2，…）.上式就是式（）对应的一阶常系数齐次线性差分方程.（）如果函数yt=φ代入式（）或（式（）），使之对t=0，1，2，…......
2023-10-27
-
高等数学第二版第六节：二阶齐次线性微分方程详细阅读
，pn-1，pn都是常数.令y=erx，那么把y及其各阶导数代入方程，得方程叫作方程的特征方程.根据特征方程的根，可以写出其对应的微分方程的通解如下：从代数学知道，n次代数方程有n个根.而特征方程的每一个根都对应着通解中的一项，且每项各含一个任意常数.这样就得到n阶常系数线性微分方程的通解：例4 求方程的通解y-2y+5y″=0.解 这里的特征方程为即r2=0.它的根是r1=r2=0和r3，4=1±2i.因此所给微分方程的通解为......
2023-10-19
相关推荐